1zoj A simple problem with integer 2|板子|分块
分块算法
算法思想
引用某次考试Problem上的(伪)Pre reading(题解):
分块算法:
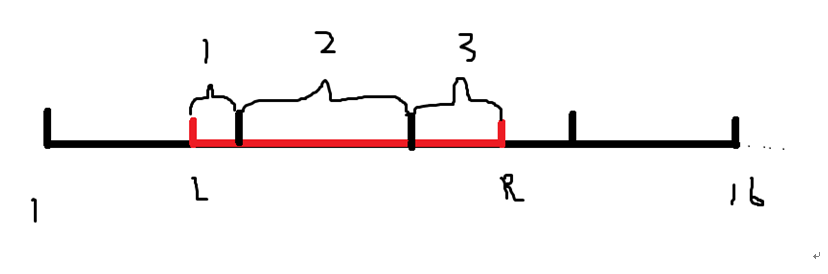
分块很像线段树,但是比线段树看起来更“暴力”一些,写起来更简单一些(期望得分80),用来维护复杂的区间信息时更容易一些。基本思想:可以把具有n个元素的集合分解成√n段,每一段的长度为√n (当然,最后一段可能不够)。对于任意一个区间操作[L,R],可将其分解成三部分。
例如当n=16,L=3,R=10:
[L,R]区间可分解为:两端可能不足一个块长度的区域(1和3),和中间的若干完整块(2)。信息维护:对于中间的若干完整块,可以采取整体操作的方式(一般打lazytag),两边的零散块采用暴力的方式。
例如:区间修改
1、计算块长度len=√n
2、预处理单点所在的块编号b [i]=(i-1)/len+1 (若编号都是从1开始)
3、暴力更新左边[L,min(b [L]*len,R)], 中间打标记(从块b [L]+1到b [R]-1),暴力更新右边(可能不存在)。。。
板子题
板子代码
#include <cstdio>
#include <iostream>
#include <cmath>
#include <algorithm>
#define LL long long
using namespace std;
void read(LL &n){
LL num=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
num=num*10+ch-'0';
ch=getchar();
}
n=num*w;
}
const int maxn=1e5+5;
LL n,m;
int blo/*每个块的长度*/,bl[maxn];//每个块的编号
LL a[maxn],tag[maxn]/*懒标记*/,sum[maxn];
//预处理
void init(){
read(n);read(m);
blo=sqrt(n);
for(int i=1;i<=n;i++){
read(a[i]);
bl[i]=(i-1)/blo+1;//计算每个节点所在的块编号
sum[bl[i]]+=a[i];
}
}
//区间和查询
LL query(int l,int r){
LL ans=0;
//暴力计算左边
for(int i=l;i<=min(bl[l]*blo,r);i++)
ans+=a[i]+tag[bl[l]];
//暴力计算右边
if(bl[l]!=bl[r])
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
ans+=a[i]+tag[bl[r]];
//整块计算中间
for(int i=bl[l]+1;i<=bl[r]-1;i++)
ans+=sum[i]+blo*tag[i];
return ans;
}
//区间修改
void update(int l,int r,LL c){
//暴力修改左边
for(int i=l;i<=min(bl[l]*blo,r);i++)
a[i]+=c,sum[bl[l]]+=c;
//暴力修改右边
if(bl[l]!=bl[r])
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
a[i]+=c,sum[bl[r]]+=c;
//整块修改中间
for(int i=bl[l]+1;i<=bl[r]-1;i++)
tag[i]+=c;
}
int main(){
init();
for(int i=1;i<=m;i++){
char ord;cin>>ord;
LL a,b;read(a);read(b);
if(ord=='Q') printf("%lld\n",query(a,b));
else{
LL c;read(c);
update(a,b,c);
}
}
return 0;
}