10.15T1 容斥原理+二项式定理优化

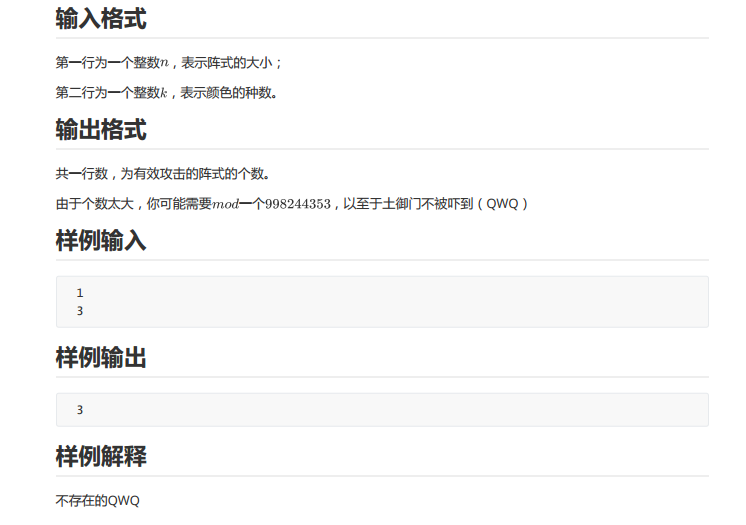
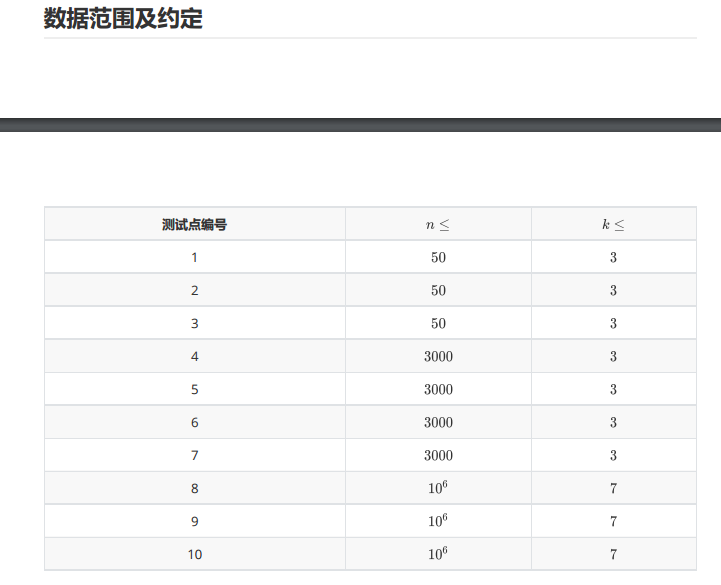
这题其实一眼就知道肯定要容斥了,分为行列单独容斥,最后交叉 的时候容斥一下就有70分了(暴力容斥)
70分题解:

code:
1 #include<iostream> 2 #include<cstdio> 3 #define N 5000006 4 using namespace std; 5 const long long mod=998244353; 6 long long n,k; 7 long long jie[N],ci[N],c[3001][3001]; 8 void pre() { 9 ci[0]=1; 10 for(int i=1; i<=n*n; i++)ci[i]=ci[i-1]*k%mod; 11 for (int i=0; i<=n; i++) 12 for (int j=0; j<=i; j++) 13 if (j==0||i==j) c[i][j]=1; 14 else c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod; 15 } 16 int main() { 17 // freopen("magic.in","r",stdin); 18 // freopen("magic.out","w",stdout); 19 cin>>n>>k; 20 pre(); 21 long long ans=0; 22 for(long long i=1; i<=n; i++) { 23 if(i&1) { 24 ans+=((ci[(n-i)*n]*c[n][i])%mod*ci[i])%mod; 25 ans+=mod; 26 ans%=mod; 27 } else { 28 ans-=((ci[(n-i)*n]*c[n][i])%mod*ci[i])%mod; 29 ans+=mod; 30 ans%=mod; 31 } 32 } 33 ans*=2; 34 for(long long i=1; i<=n; i++) { 35 for(long long j=1; j<=n; j++) { 36 if((i+j)&1) { 37 ans+=(ci[((n-(i+j))*n)+i*j]*c[n][i])%mod*c[n][j]%mod*k%mod; 38 ans%=mod; 39 } else { 40 ans-=(ci[((n-(i+j))*n)+i*j]*c[n][i])%mod*c[n][j]%mod*k%mod; 41 ans=(ans+mod)%mod; 42 } 43 } 44 } 45 cout<<ans; 46 return 0; 47 }
100分:

官方code:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<set> 7 #include<queue> 8 #include<ctime> 9 #define MAXN 200005 10 #define ll long long 11 #define maxn 15 12 #define maxs 1000005 13 #define inf 1e9 14 #define eps 1e-9 15 using namespace std; 16 inline char gc() { 17 static char now[1<<16],*S,*T; 18 if (T==S) { 19 T=(S=now)+fread(now,1,1<<16,stdin); 20 if (T==S) return EOF; 21 } 22 return *S++; 23 } 24 inline ll readlong() { 25 ll x=0,f=1; 26 char ch=getchar(); 27 while(ch<'0'||ch>'9') { 28 if(ch=='-')f=-1; 29 ch=getchar(); 30 } 31 while(ch>='0'&&ch<='9') { 32 x*=10; 33 x+=ch-'0'; 34 ch=getchar(); 35 } 36 return x*f; 37 } 38 const int N=1000005; 39 const int mod=998244353; 40 ll res,ans,n,k; 41 ll fac[N],inv[N]; 42 void update(ll &x,ll y) { 43 x+=y; 44 if(x<0) { 45 x+=mod; 46 } 47 if(x>=mod) { 48 x-=mod; 49 } 50 } 51 ll ksm(ll x,ll k) { 52 update(x,0); 53 ll ret=1; 54 ll ans=x; 55 while(k) { 56 if(k&1) { 57 ret=ret*ans%mod; 58 } 59 ans=ans*ans%mod; 60 k>>=1; 61 } 62 return ret; 63 } 64 ll calc(ll x,ll y) { 65 if(x<y) { 66 return 0; 67 } 68 if(x==y) { 69 return 1; 70 } 71 return 1ll*fac[x]*inv[y]%mod*inv[x-y]%mod; 72 } 73 int main() { 74 freopen("magic.in","r",stdin); 75 freopen("magic.out","w",stdout); 76 n=readlong(); 77 k=readlong(); 78 fac[0]=1; 79 for(int i=1; i<=n; i++)fac[i]=fac[i-1]*i%mod; 80 inv[n]=ksm(fac[n],mod-2); 81 for(int i=n-1; i>=0; i--)inv[i]=inv[i+1]*(i+1)%mod; 82 for(int i=1; i<=n; i++) { 83 int a=1ll*calc(n,i)*ksm(-1,i+1)%mod; 84 int x=ksm(k,(1ll*n*(n-i)+i)%(mod-1)); 85 update(ans,1ll*a*x%mod); 86 } 87 ans=2*ans%mod; 88 for(int i=0; i<n; i++) { 89 int tmp=mod-ksm(k,i); 90 int x=(ksm(tmp+1,n)+mod-ksm(tmp,n))%mod; 91 int a=1ll*calc(n,i)*ksm(-1,i+1)%mod; 92 update(res,1ll*a*x%mod); 93 } 94 res=k*res%mod; 95 printf("%lld\n",(ans+res)%mod); 96 return 0; 97 }
本人code:
1 #include<iostream> 2 #include<cstdio> 3 #define N 1000005 4 using namespace std; 5 const long long mod=998244353; 6 long long n,k; 7 long long jie[N],inv[N]; 8 long long ksm(long long a,long long b) { 9 long long ans=1; 10 for(; b; b>>=1) { 11 if(b&1) { 12 ans*=a; 13 ans%=mod; 14 } 15 a*=a; 16 a%=mod; 17 } 18 return ans; 19 } 20 long long read() { 21 long long x=0,f=1; 22 char c=getchar(); 23 while(!isdigit(c)) { 24 if(c=='-')f=-1; 25 c=getchar(); 26 } 27 while(isdigit(c)) { 28 x=(x<<3)+(x<<1)+c-'0'; 29 c=getchar(); 30 } 31 return x*f; 32 } 33 long long C(long long a,long long b) { 34 return (((jie[a]*inv[b])%mod*inv[a-b])%mod+mod)%mod; 35 } 36 void pre() { 37 jie[0]=1; 38 for(long long i=1; i<=n; i++)jie[i]=jie[i-1]*i%mod; 39 inv[n]=ksm(jie[n],mod-2); 40 for(long long i=n-1; i>=0; i--)inv[i]=inv[i+1]*(i+1)%mod; 41 } 42 int main() { 43 n=read(),k=read(); 44 pre(); 45 long long ans=0; 46 for(long long i=1; i<=n; i++) { 47 if(i&1) { 48 ans+=C(n,i)*ksm(k,(n-i)*n)%mod*ksm(k,i); 49 ans+=mod; 50 ans%=mod; 51 } else { 52 ans-=C(n,i)*ksm(k,(n-i)*n)%mod*ksm(k,i); 53 ans+=mod; 54 ans%=mod; 55 } 56 } 57 ans*=2; 58 ans%=mod; 59 for(long long i=0; i<n; i++) { 60 if(i&1) { 61 long long temp1=C(n,i); 62 long long temp2=(1-ksm(k,i)+2*mod)%mod; 63 long long temp3=ksm(k,i); 64 temp2=ksm(temp2,n); 65 temp3=ksm(temp3,n); 66 if(n&1){ 67 temp3=-temp3; 68 } 69 ans+=k*(temp1*(temp2-temp3)%mod+mod)%mod; 70 ans+=mod; 71 ans%=mod; 72 } else { 73 long long temp1=C(n,i); 74 long long temp2=(1-ksm(k,i)+2*mod)%mod; 75 long long temp3=ksm(k,i); 76 temp2=ksm(temp2,n); 77 temp3=ksm(temp3,n); 78 if(n&1){ 79 temp3=-temp3; 80 } 81 ans-=k*(temp1*(temp2-temp3)%mod+mod)%mod; 82 ans+=mod; 83 ans%=mod; 84 } 85 } 86 cout<<ans; 87 return 0; 88 }
over

