10.08 特教的理性愉悦 树上预处理乱搞+式子推理
Description
某正教授级特级教师忽然想自娱自乐。于是他准备在纸上画一棵树。这棵树开始时只有N个点,然后特教开始逐条画上一些带权无向边(保证任意时刻纸上的任意两点间至多有一条路径),直到最后形成一棵树。
为了达到理性愉悦的目的,特教在加边的过程中可能会随意选取两个点并取出连接它们的路径,计算该路径上所有点对距离之和(如果已经有路径连通)。1--[5]--2--[3]--3--[2]--4(说明:[]内为边长),共有 (1, 2)(1, 3)(1, 4)(2, 3)(2, 4)(3, 4)六个点对,距离之和为 5+8+10+3+5+2 = 33。现在特教需要检验他的答案是否正确,于是想请你编个程序帮他验算一下。
为了达到理性愉悦的目的,特教在加边的过程中可能会随意选取两个点并取出连接它们的路径,计算该路径上所有点对距离之和(如果已经有路径连通)。1--[5]--2--[3]--3--[2]--4(说明:[]内为边长),共有 (1, 2)(1, 3)(1, 4)(2, 3)(2, 4)(3, 4)六个点对,距离之和为 5+8+10+3+5+2 = 33。现在特教需要检验他的答案是否正确,于是想请你编个程序帮他验算一下。
Input
第一行为两个正整数 N , M ,表示树的点数和操作数。
第二行开始的 M 行为 M 个操作的具体内容,分为两种:
(1)“1 u v w”,表示加一条连接 u 和 v 的边,边权为w;
(2)“2 u v”,表示询问当前树上u到 v 的路径上所有点对距离之和,如果还不连通则输出-1。
输入数据保证加边合法,u!= v,边权w为正整数,且其中恰有N-1 个(1)操作以及至少1个(2)操作,即 M>=N
第二行开始的 M 行为 M 个操作的具体内容,分为两种:
(1)“1 u v w”,表示加一条连接 u 和 v 的边,边权为w;
(2)“2 u v”,表示询问当前树上u到 v 的路径上所有点对距离之和,如果还不连通则输出-1。
输入数据保证加边合法,u!= v,边权w为正整数,且其中恰有N-1 个(1)操作以及至少1个(2)操作,即 M>=N
Output
对于每个(2)操作输出一行,表示询问的结果。
Sample Input

Sample Output
Hint

题解:这题我写了5个小时。。。。。OTZ
维护一个func数组代表根节点到该点的dis之和
维护g数组代表一个点到他各个父亲的距离之和
用一个sumg维护树上g的前缀和
dep维护深度,f维护父亲
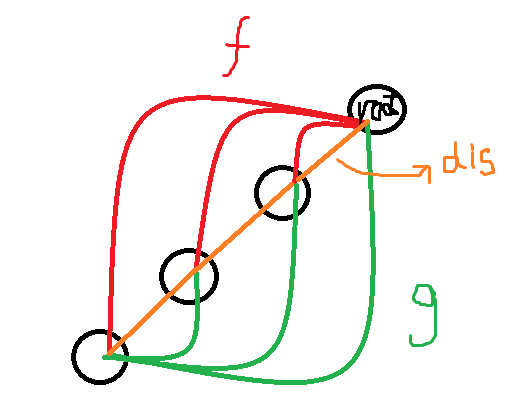
然后我们对于询问的区间显然可以以lca作为分界线
显然就产生了跨过lca的值和在单边求和值
跨过lca的话,
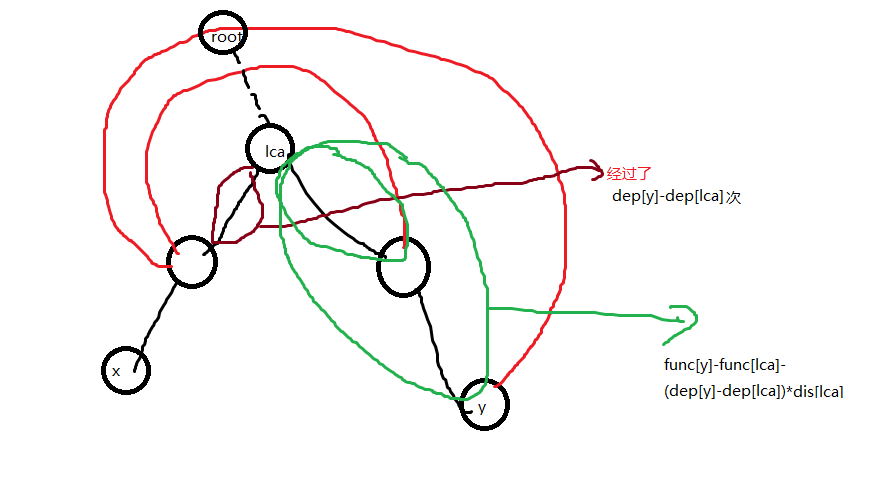
对于每个统计,合并同类项的话可以得到一个跨过去的总值公式:
1 long long kua=sizright*(func[x]-func[father]-sizleft*dis[father])+sizleft*(func[y]-func[father]-sizright*dis[father]);
注:这里的father就是lca
然后对于每一边来说就要用到g数组了,画图来理解更容易一点
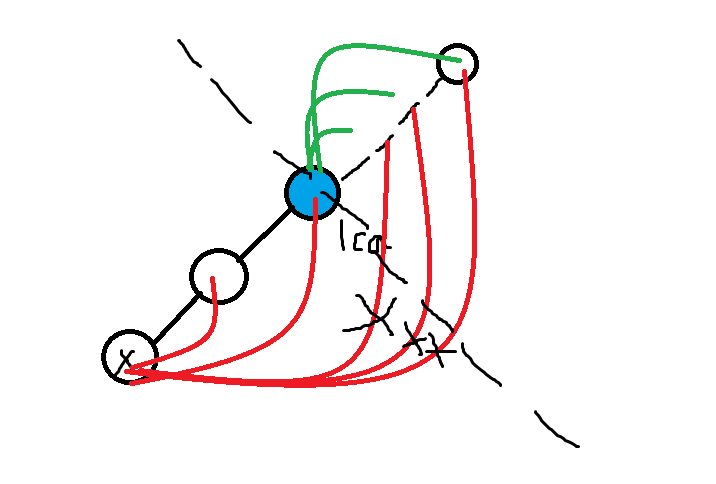
不难看出方程是
1 long long ownleft=sumg[x]-sumg[father]-g[father]*sizleft+dep[father]*dis[father]*sizleft-dep[father]*(func[x]-func[father]); 2 long long ownright=sumg[y]-sumg[father]-g[father]*sizright+dep[father]*dis[father]*sizright-dep[father]*(func[y]-func[father]);
所以总值就出来了,加在一起
code:
1 #include<iostream> 2 #include<cstdio> 3 #define N 300006 4 using namespace std; 5 struct node { 6 long long u,v,w; 7 } e[N],q[N]; 8 long long fa[N]; 9 long long n,m; 10 long long find(long long x) { 11 if(x!=fa[x])return fa[x]=find(fa[x]); 12 return fa[x]; 13 } 14 void merge(long long x,long long y) { 15 long long f1=find(x),f2=find(y); 16 if(f1!=f2) { 17 fa[f1]=f2; 18 } 19 } 20 long long first[N],nxt[N],cnt; 21 void add(long long u,long long v,long long w) { 22 e[++cnt].u=u; 23 e[cnt].v=v; 24 e[cnt].w=w; 25 nxt[cnt]=first[u]; 26 first[u]=cnt; 27 } 28 long long dep[N],f[N][30]; 29 long long lca(long long x,long long y) { 30 if(dep[y]>dep[x])swap(x,y); 31 for(long long i=19; i>=0; i--) { 32 if(dep[f[x][i]]>=dep[y]) 33 x=f[x][i]; 34 if(x==y)return y; 35 } 36 for(long long i=19; i>=0; i--) { 37 if(f[x][i]==f[y][i])continue; 38 x=f[x][i],y=f[y][i]; 39 } 40 return f[x][0]; 41 } 42 long long dis[N],func[N],g[N],sumg[N]; 43 void dfs(long long x) { 44 for(long long i=first[x]; i; i=nxt[i]) { 45 long long v=e[i].v; 46 if(v==f[x][0])continue; 47 dep[v]=dep[x]+1; 48 f[v][0]=x; 49 dis[v]=dis[x]+e[i].w; 50 func[v]=func[x]+dis[v];//这个数组是用来记录这个点上面所有父亲到根节点的距离和 51 g[v]=g[x]+dep[v]*e[i].w; 52 sumg[v]=sumg[x]+g[v]; 53 dfs(v); 54 } 55 } 56 long long tot; 57 int main() { 58 ios::sync_with_stdio(false); 59 cin>>n>>m; 60 for(long long i=1; i<=n; i++)fa[i]=i; 61 for(long long i=1; i<=m; i++) { 62 long long op; 63 cin>>op; 64 if(op==1) { 65 long long u,v,w; 66 cin>>u>>v>>w; 67 add(u,v,w); 68 add(v,u,w); 69 merge(u,v); 70 } else { 71 long long u,v; 72 cin>>u>>v; 73 q[++tot].u=u; 74 q[tot].v=v; 75 if(find(u)!=find(v)) { 76 q[tot].w=1; 77 } 78 } 79 } 80 f[1][0]=1; 81 dep[1]=0; 82 dfs(1); 83 // for(long long i=1;i<=n;i++){ 84 // cout<<"num->"<<i<<" dep->"<<dep[i]<<" dis->"<<dis[i]<<" father->"<<f[i][0]<<" func->"<<func[i]<<" g->"<<g[i]<<" sumg->"<<sumg[i]<<'\n'; 85 // } 86 for(long long i=1; i<=20; i++) { 87 for(long long j=1; j<=n; j++) { 88 f[j][i]=f[f[j][i-1]][i-1]; 89 } 90 } 91 for(long long i=1; i<=tot; i++) { 92 long long ans=0; 93 if(q[i].w) { 94 cout<<-1<<'\n'; 95 continue; 96 } 97 long long u=q[i].u,v=q[i].v; 98 long long father=lca(u,v); 99 long long x=u,y=v; 100 // cout<<"x->"<<u<<" y->"<<v<<" lca->"<<father<<" sizleft->"<<dep[x]-dep[father]<<" sizright->"<<dep[y]-dep[father]<<endl; 101 long long sizleft=dep[x]-dep[father],sizright=dep[y]-dep[father]; 102 long long kua=sizright*(func[x]-func[father]-sizleft*dis[father])+sizleft*(func[y]-func[father]-sizright*dis[father]); 103 //cout<<g[x]-g[father]-dep[father]*(dis[x]-dis[father])<<'\n'; 104 long long ownleft=sumg[x]-sumg[father]-g[father]*sizleft+dep[father]*dis[father]*sizleft-dep[father]*(func[x]-func[father]); 105 long long ownright=sumg[y]-sumg[father]-g[father]*sizright+dep[father]*dis[father]*sizright-dep[father]*(func[y]-func[father]); 106 cout<<kua+ownleft+ownright<<'\n'; 107 //long long kuaright= 108 //long long kua=kualeft+kuaright; 109 //cout<<"kua->"<<kua<<endl; 110 //cout<<ans<<'\n'; 111 } 112 } 113 /*sumg[x]-sumg[lca]-sizzuo*g[lca]-dep[lca]*f[x]+sizzuo*dep[lca]*dis[lca]; 114 sizyou*(f[x]-f[lca]-sizzuo*dis[lca])+sizzuo(f[y]-f[lca]-sizyou*dis[lca]);*/
over!



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步