10.03T3 期望DP+修改

3、摧毁树状图（graph）

题目描述：

自从上次神刀手帮助蚯蚓国增添了上千万人口（蚯口？），蚯蚓国发展得越来越繁荣了！最近，他们在地下发现了一些神奇的纸张，经过仔细研究，居然是D国X市的超级计算机设计图纸！这台计算机叫做‘树状图’，由n个计算节点与n-1条可以双向通信的网线连接而成，所有计算节点用不超过n的正整数编号。顾名思义，这形成了一棵树的结构。蚯蚓国王已在图纸上掌握了这棵树的完整信息，包括n的值与n-1条网线的连接信息。于是蚯蚓国王决定，派出蚯蚓国最强大的两个黑客，小P和小H，入侵‘‘树状图’’，尽可能地摧毁它。小P和小H精通世界上最好的编程语言，经过一番商量后，他们决定依次采取如下的步骤：

1)整棵树的每个计算节点有一个故障率P，表示有P的几率会摧毁掉这个节点。显而易见这个时候这个图的连通块个数会增加。国王（或者是小P/H）会派人询问当前树状图联通块的期望个数。
2)小P和小H水平并不是想象中那么高，他们只能修改某个点的故障率，而且（他们甚至不知道故障率提升越高越好）他们也想知道当前树状图联通块的期望个数。

3)此时你不需要指挥他们入侵了，只需要计算每次修改节点故障率后，剩下的连通块的期望个数即可。

 

注意：被摧毁的节点不算入连通块的数量中。

 

 

输入格式：

第一行一个正整数n，表示节点数。

第二行n个实数,表示第i个点的故障率。

第3行到第3+n-2行每行两个整数a,b,（1<=a,b<=n）表示啊a,b之间有一条边。

接下来一个正整数m，表示修改次数。

接下来m行，每行一个正整数a和一个实数c，表示将节点a的故障率修改为c。

 

输出格式：

m行，表示每次修改过后连通块的期望值。

 

 

样例输入1：

3

0.23 0.40 0.50

1 2

1 3

1

1 0.3

 

样例输入2：

5

0.50 0.20 0.90 0.50 0.50

2 1

5 3

3 1

4 3

5

5 0.50

4 0.10

2 0.40

4 0.80

1 0.30

 

样例输出1：

1.0300

 

样例输出2：

1.8500

2.2100

2.1100

1.4800

1.5400

 

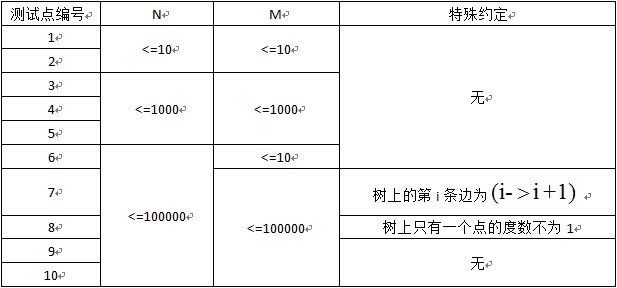
数据规模与约定：

 

 

 

 

 

 

HCH的官方题解：

我们考虑做有根树的DP。设1为根。

我们设p[v]为v节点消失的概率，设f[v][0],f[v][1]分别表示v节点被破坏/没被破坏时的连通块期望值。

f[v][0]=p[v]\cdot \sum (f[sn][0]+f[sn][1])

f[v][1]=(1-p[v])\cdot (1+\sum (f[sn][0]+f[sn][1]-(1-p[sn])))

解释一下f[v][1]的转移方程：因为如果v节点没有被破坏，并且儿子节点sn也没有被破坏，那么连通块的个数会减少，减少的数量就是sn所在的连通块的期望，也就是1-p[sn]。

当然我们不可能每次询问了就DFS一遍计算，所以我们需要再研究一下递推式。

我们先只考虑4号点对答案的贡献。我么按照递推式模拟一遍。

最后答案就是f[1][0]+f[1][1]，也就是p[3]*(1-p[4])。推广到一般情况：v对答案的贡献就是p[fa[v]]*(1-p[v])，特别地，设p[0]=1（0是1的父亲）。

知道这个结论过后维护起来就特别方便了。我们记sum[v]=\sum (1-p[sn])。修改一个点的概率时就相应地修改值就行了（具体见代码）。

估计看不懂在说什么

首先我们考虑如何求解不操作的情况。

考虑期望的线性性，我们统计每一个节点对答案的负贡献。

首先，假装每一个节点都是一个连通块。

对于节点 x ，如果他消失了，那么连通块个数 -1，由于他消失的概率是 px ，他对期望的负贡献为 pi 。

对于无序数对 (x,y) ，如果 x 和 y 有边连接，那么，当且仅当他们都存在，才会对连通块个数产生负贡献，所以它对期望的负贡献为 (1−px)(1−py) 。

完成了这个问题之后，修改操作也变得简单了。

首先给树定根。然后，只需要对于每一个节点 x 维护一个 vson[x] 代表其所有儿子的 (1−py)之和。修改操作就变的简单了。

时间复杂度 O(n) 。

code：

 1 #include<iostream>
 2 #include<cstdio>
 3 #define N 1000005
 4 using namespace std;
 5 struct node{
 6     int u,v;
 7 }e[N];
 8 double ans;
 9 int first[N],nxt[N],cnt;
10 void add(int u,int v){
11     e[++cnt].u=u;
12     e[cnt].v=v;
13     nxt[cnt]=first[u];
14     first[u]=cnt;
15 }
16 double add1[N],add2[N],sum[N],p[N];
17 int fa[N];
18 void dfs(int x,int father){
19     fa[x]=father;
20     add1[x]=p[x];
21     for(int i=first[x];i;i=nxt[i]){
22         int v=e[i].v;
23         if(v==father)continue;
24         sum[x]+=(1.0-p[v]);
25         dfs(v,x);
26     }
27     add2[x]=1.0*(1-p[x])*sum[x];
28     ans-=add1[x]+add2[x];
29 }
30 int main(){
31     ios::sync_with_stdio(false);
32     int n;
33     cin>>n;p[0]=1.0;
34     ans=n*1.0;
35     for(int i=1;i<=n;i++)cin>>p[i];
36     for(int i=1;i<n;i++){
37         int u,v;
38         cin>>u>>v;
39         add(u,v);
40         add(v,u);
41     }
42     dfs(1,0);
43     int q;cin>>q;
44     while(q--){
45         int a;
46         double c;
47         cin>>a>>c;
48         int father=fa[a];
49         ans+=p[a];
50         ans+=(1.0-p[a])*sum[a];
51         ans+=(1.0-p[father])*(1-p[a]);
52         sum[fa[a]]-=1-p[a];
53         p[a]=c;
54         ans-=p[a];
55         ans-=(1.0-p[a])*sum[a];
56         ans-=(1.0-p[father])*(1-p[a]);
57         sum[fa[a]]+=1-p[a];
58         printf("%.4lf\n",ans);
59     }
60     return 0;
61 }

over

posted @ 2018-10-03 17:57  saionjisekai  阅读(96)  评论(0)    收藏  举报