9.30T1 打表证明排序不等式/柯西不等式+逆元

                                                                                                                    任务

【问题描述】


小A有n个任务，每个任务有一定的价值si

定义一个三元组（i，j, k）如果三个ijk任务同时被选择，那么就会提供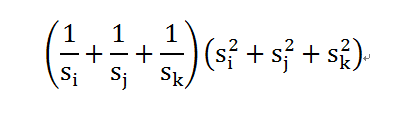的优美程度

反之，若其中至少有一个任务没有被选择，那么会提供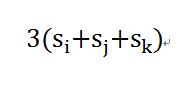的优美程度

现在，小A可以人已决定选择若干个任务，对于所有的有序可重三元组，他想要知道他能得到的最大优美程度和是多少，以及在最大化优美程度的基础上，他想知道选择的任务数量最少是多少

为了避免精度问题，你需要输出对1000000007取模的值，注意你需要输出的是最大优美度在mod意义下的值，不是最大模意义下的优美程度

【输入】

输入包括三行

第一行是一个数字n，表示任务总共的任务数量

第二行包括n个书，第 i 个数字si表示每个任务的价值

【输出】 

第一行是最大优美程度

第二行是选择的任务数量

【样例输入】

3

1 2 3

【样例输出】

624

3

【数据范围】

对于10%的数据，保证n<=5
对于40%的数据，保证n<=10
对于70%的数据，保证n<=500
对于100%的数据，保证n<=10000000,1<=si<=n

 

 

 

首先我们要比较两个式子，根据柯西不等式变换可以得到以下证明

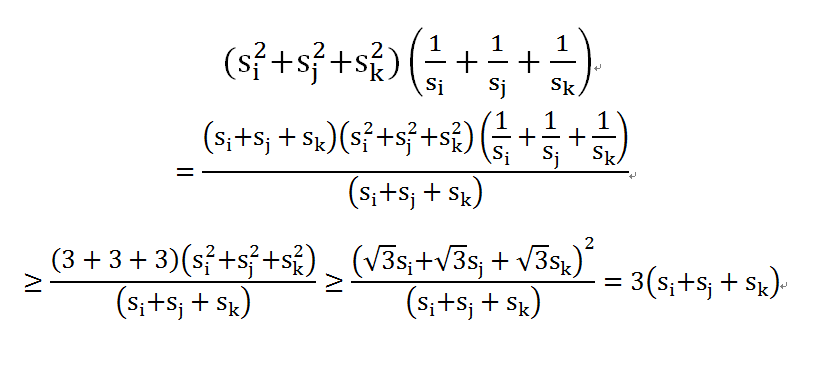
（word敲公式真TM麻烦）

那么任务就要选一定都要选才会是最大

那么我们再看取等号的条件实际上是所有的数字都相等，当这个时候干脆什么都不取，满足了最大同时最少

那么计算的时候我们要展开分开求和

原始展开拆成两个部分

 

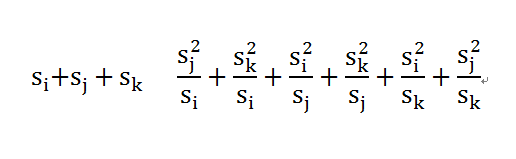
code：

 1 #include<iostream>
 2 #include<cstdio>
 3 #define N 10000005
 4 using namespace std;
 5 long long inv[N],suminv[N],sumsq[N],sum[N];
 6 long long a[N];
 7 const long long mod=1e9+7;
 8 inline void pre(long long n){
 9     inv[1]=1;
10     for(long long i=2;i<=n+1;i++){
11         inv[i]=((-(mod/i)*inv[mod%i])%mod+mod)%mod;
12     }
13 }
14 int main(){
15     freopen("problem.in","r",stdin);
16     freopen("problem.out","w",stdout);
17     long long n;scanf("%lld",&n);
18     pre(n);
19 //    for(long long i=1;i<=n+1;i++)cout<<inv[i]<<endl;
20     long long flag=0;
21     for(long long i=1;i<=n;i++){
22         scanf("%lld",&a[i]);
23         sumsq[i]=(sumsq[i-1]+(a[i]*a[i])%mod)%mod;
24         sum[i]=(sum[i-1]+a[i])%mod;
25         suminv[i]=(suminv[i-1]+inv[a[i]])%mod;
26         if(i>1){
27             if(a[i]!=a[i-1])flag=1;
28         }
29     }
30     long long ans=((3*n*n)%mod*sum[n])%mod+(6*n)%mod*suminv[n]%mod*(sumsq[n]%mod)%mod;
31     cout<<ans%mod<<endl;
32     if(flag)cout<<n;
33     else cout<<0;
34 }

over

posted @ 2018-09-30 13:22  saionjisekai  阅读(99)  评论(0)    收藏  举报