9.27T1 组合数+容斥原理

1.分特产2414

 (cut)

【问题描述】

JYY 带队参加了若干场ACM/ICPC 比赛，带回了许多土特产，要分给实验室的同学们。

JYY 想知道，把这些特产分给N 个同学，一共有多少种不同的分法？当然，JYY 不希望任何一个同学因为没有拿到特产而感到失落，所以每个同学都必须至少分得一个特产。

例如，JYY 带来了2 袋麻花和1 袋包子，分给A 和B 两位同学，那么共有4 种不同的

分配方法：

A：麻花，B：麻花、包子

A：麻花、麻花，B：包子

A：包子，B：麻花、麻花

A：麻花、包子，B：麻花

【输入】

输入数据第一行是同学的数量N 和特产的数量M。

第二行包含M 个整数，表示每一种特产的数量。

N, M 不超过1000，每一种特产的数量不超过1000.

【输出】

输出一行，不同分配方案的总数。由于输出结果可能非常巨大，你只需要输出最终结果

MOD 1,000,000,007 的数值就可以了。

【样例输入】

5 4
1 3 3 5

 

 

 

题目来源于JSOI2011

我今天早上才做了一道容斥原理的题目。。。结果就考了，我还是没有做起，考完之后看了下成绩还是倒数第二，倒数第一爆了0

光是这一道题只有后面的几个人没写起，其他人全AC

所有的物品，将其划分成n部分，每部分不能为空，问总的方案数
可以如果利用插板法的话，把n个相同的小球放到m个不同的盒子里有C（n+m−1，m−1）种方案，不过这个只能求出允许空的方案数，对每一种特产都讨论的话，总方案数即为根据容斥原理，答案应该为至少0个盒子为空的-至少1个盒子为空的+至少2个盒子为空的-…至少n个盒子为空的
那么我们可以每一次强制i个盒子为空，剩余的再像上面一样选就行了

答案就是

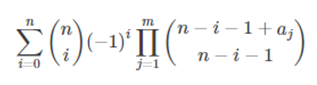
上面是官方解法，下面谈谈我的感受

这道题其实当时有那么一丝丝的感受是容斥原理，但是我也不知道怎么容斥，但我也没想到是枚举多少个空的来进行容斥

首先我们考虑把每一种物品分开来处理，也就是一类一类的处理，最后把他们相乘就是当前的状态

首先我们明显知道如果m个小球给n个人（允许空出来），答案就是C[n-1][n+m-1]。这个还是知道的

显然我们要排除有空的情况，对于空出来的情况我们有空1人，2,3,4.。。。直到n

至少空 i 个人，那么就剩余 n-i 个人，状态数就是C[n-i-1][n+m-1-i]前面必须还要乘上C[i][n]代表选哪几个空着

然后跑一边容斥原理。。。。

显然我做不起。。。。慢慢写吧。。。。

code：

#include<iostream>
#include<cstdio>
using namespace std;
int c[2005][2005];
const int mod=1e9+7;
int s[5000];
int main(){
    for(int i=0;i<=2000;i++)c[i][0]=1; 
    for(int i=1;i<=2000;i++)
        for(int j=1;j<=2000;j++)
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
    int n,m;
    cin>>n>>m;
    long long ans=0;
    for(int i=1;i<=m;i++)cin>>s[i];
    for(int i=0;i<=n;i++){//枚举至少几个人是空的 
        long long now=1;
        for(int j=1;j<=m;j++){
            now*=c[n-i-1+s[j]][n-i-1];
            now%=mod;
        }
        if(i%2){
            ans-=c[n][i]*now;
            ans=(ans+mod)%mod;
        }
        else{
            ans+=c[n][i]*now;
            ans%=mod;
        }
    } 
    ans+=mod,ans%=mod;
    cout<<ans;
    return 0;
}

over