9.26T2
2.失意
(failure)
【问题描述】
n 条线段,选择 m 条使相交部分最大。
【输入】
第一行num代表数据组数
下面一行是n,m
接下来就是n行代表每一条线段的左端点和右端点
【输出】
输出一个数字代表最长的覆盖长度
接下来一行输出要找哪几条线段
【输入样例】
4
6 3
3 8
4 12
2 6
1 10
5 9
11 12
【输出样例】
4
1 2 4
【数据规模与约定】
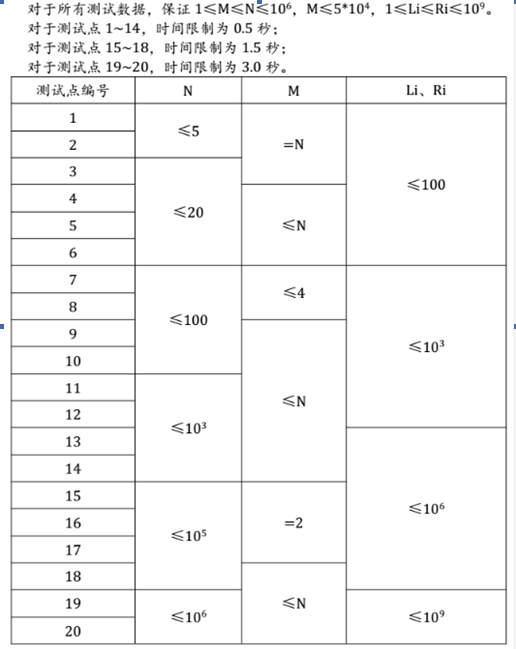
这一道题一开始写的是dp,没发现其实这道题拥有后效性,然后因为SPJ拿了18分就直接跑路了
这道题还是一道贪心(对于线段的题目一般都是这样好处理)
显然我们先对左端点进行排序
然后把前m条线段扔进一个堆里面,初始化我们的答案(也就是最小的右端点减去最大的左端点)
接下来对于剩下的线段,我们每次扔进去一条线段,然后取出右端点最小的值,更新完答案之后就把这个点对应的线段扔掉就行了,注意这个时候我们的左端点其实是当前线段的最大的左端点大小
最后有一个非常坑的地方就是如果答案小于0就是0(因为根本就没有)
至于输出方案
输出m个左端点比ans的左端点小,比右端点大的线段就可以了
我太菜了QAQ555,lzy秒切这道题555(lzy今天297分)
代码调了好久。。。。Lemon真是好啊
10.28UPDATE:想了下万事先排序,然后讨论以当前线段作为一个端点的最大值可以是多少,为了维持m个所以要弹出最小的右端点
code:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<queue> 5 #define N 1000005 6 using namespace std; 7 struct node{ 8 int l,r,id; 9 }e[N]; 10 priority_queue<node>q; 11 bool operator<(node a,node b){ 12 return a.r>b.r; 13 } 14 bool cmp(node a,node b){ 15 return a.l<b.l; 16 } 17 int g[1000005],tot; 18 int main(){ 19 freopen("failure.in","r",stdin); 20 freopen("failure.out","w",stdout); 21 // ios::sync_with_stdio(false); 22 int num;cin>>num; 23 int n,m;cin>>n>>m; 24 for(int i=1;i<=n;i++){ 25 scanf("%d%d",&e[i].l,&e[i].r); 26 e[i].id=i; 27 } 28 sort(e+1,e+n+1,cmp);//按照左端点进行排序 29 // cout<<endl<<endl; 30 // for(int i=1;i<=n;i++)cout<<e[i].l<<" "<<e[i].r<<endl; 31 for(int i=1;i<=m;i++)q.push(e[i]);//左端点排序后直接扔进去 32 int ansl,ansr,ans; 33 ansl=e[m].l; 34 ansr=q.top().r; 35 ans=ansr-ansl; 36 // cout<<" "<<ansl<<" "<<ansr<<" "<<ans<<endl; 37 // cout<<"throw"<<" "<<q.top().l<<" "<<q.top().r<<endl; 38 q.pop(); 39 for(int i=m+1;i<=n;i++){ 40 q.push(e[i]); 41 node t=q.top(); 42 int tempr=t.r; 43 // cout<<" "<<e[i].l<<" "<<tempr<<" "<<ans<<endl; 44 // cout<<"throw"<<" "<<q.top().l<<" "<<q.top().r<<endl; 45 q.pop(); 46 if(tempr-e[i].l>ans){ 47 ans=tempr-e[i].l; 48 ansl=e[i].l; 49 ansr=tempr; 50 } 51 }if(ans<0){ 52 ans=0; 53 } 54 cout<<ans; 55 puts(""); 56 for(int i=1;i<=n;i++){ 57 if(e[i].l<=ansl&&e[i].r>=ansr)g[++tot]=e[i].id; 58 } 59 sort(g+1,g+tot+1); 60 for(int i=1;i<=m;i++)printf("%d ",g[i]); 61 return 0; 62 }
over


