[2019杭电多校第二场][hdu6598]Harmonious Army(最小割)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6598
题意是说一个军队有n人,你可以给他们每个人安排战士或者法师的职业,有m对人有组合技,组合技的信息是A,B,C,代表如果这两个人是两个战士,则组合技威力为A,一个战士一个法师,威力为B,其中B=A/4+C/3,两个法师,威力为C,求最大的威力。
很网络流的题目,那就流呗XD
先考虑如果每个人可以选择两个职业,则威力为$sum=\sum_{i=1}^{n}(a[i]+b[i]+c[i])$
如果不能选择两个职业,则可以看成选择两个职业的答案减去网络中的最小割。
则我们向着最小割的方向思考。
然后我们先考虑连通性,即所有点连战士(看成源点)和法师(看成汇点),并且有关系的点相互连接。
然后看下面的图(s为源点,t为汇点,x,y为一对关系)
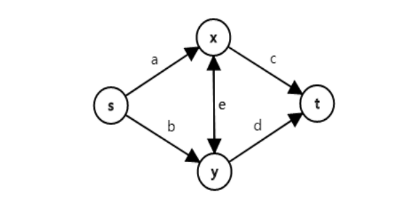
然后考虑权值:
如果x选择战士,y选择战士,则a+b=B+C(割掉B,C的威力)
如果x选择法师,y法师战士,则c+d=B+A(割掉A,B的威力)
如果x选择战士,y选择法师,则a+e+d=A+C(割掉A,C的威力)
如果x选择法师,y选择战士,则b+e+c=A+C(割掉A,C的威力)
然后可以得到一组解a=b=(A+B)/2,c=d=(C+B)/2,e=(A+C)/2-B。
然后就可以愉快的建图。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<algorithm> 5 #include<cstring> 6 #include<string> 7 #include<queue> 8 using namespace std; 9 typedef long long ll; 10 const int maxn = 2e5 + 10; 11 const ll inf = 1e18; 12 struct node { 13 int e, next; 14 double w; 15 }edge[maxn]; 16 int head[maxn], len; 17 int d[maxn]; 18 void init() { 19 memset(head, -1, sizeof(head)); 20 len = 0; 21 } 22 void add(int s, int e, double w) { 23 edge[len].e = e; 24 edge[len].w = w; 25 edge[len].next = head[s]; 26 head[s] = len++; 27 } 28 bool bfs(int s, int e) { 29 queue<int>q; 30 memset(d, 0, sizeof(d)); 31 d[s] = 1; 32 q.push(s); 33 while (!q.empty()) { 34 int x = q.front(); q.pop(); 35 for (int i = head[x]; i != -1; i = edge[i].next) { 36 int y = edge[i].e; 37 if (edge[i].w && !d[y]) { 38 d[y] = d[x] + 1; 39 q.push(y); 40 } 41 } 42 } 43 return d[e]; 44 } 45 double dfs(int x, int e, double limit) { 46 if (x == e) 47 return limit; 48 double add, ans = 0; 49 for (int i = head[x]; i != -1; i = edge[i].next) { 50 int y = edge[i].e; 51 if (d[y] == d[x] + 1 && edge[i].w) { 52 add = dfs(y, e, min(edge[i].w, limit)); 53 edge[i].w -= add; 54 edge[i ^ 1].w += add; 55 ans += add; 56 limit -= add; 57 if (!limit) 58 break; 59 } 60 } 61 if (!ans) 62 d[x] = -1; 63 return ans; 64 } 65 double dinic(int s, int e) { 66 double ans = 0; 67 while (bfs(s, e)) 68 ans += dfs(s, e, inf); 69 return ans; 70 } 71 int main() { 72 int n, m; 73 while (scanf("%d%d", &n, &m) != EOF) { 74 init(); 75 int s = n + 1, t = n + 2; 76 ll sum = 0; 77 for (int i = 1; i <= m; i++) { 78 ll x, y; 79 double a, b, c; 80 scanf("%lld%lld%lf%lf%lf", &x, &y, &a, &b, &c); 81 add(s, x, (a + b) / 2); 82 add(x, s, 0); 83 add(s, y, (a + b) / 2); 84 add(y, s, 0); 85 add(x, t, (b + c) / 2); 86 add(t, x, 0); 87 add(y, t, (b + c) / 2); 88 add(t, y, 0); 89 add(x, y, -b + (a + c) / 2); 90 add(y, x, 0); 91 add(y, x, -b + (a + c) / 2); 92 add(x, y, 0); 93 sum += a + b + c; 94 } 95 ll ans = round(sum - dinic(s, t)); 96 printf("%lld\n", ans); 97 } 98 }

