相交 - 两线段是否相交 - 跨立方式
快速排斥
快速排除不可能相交的情况
1
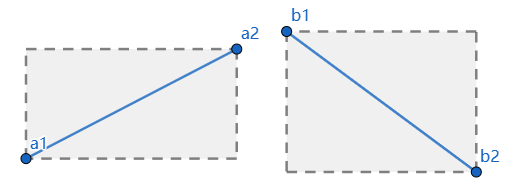
2
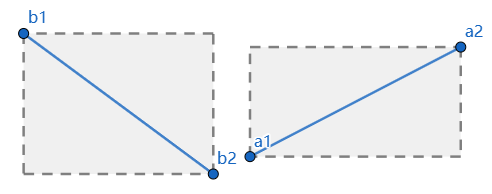
3, 4
但类似下面这类情况，矩形区域相交，但线段没相交的就无法处理了
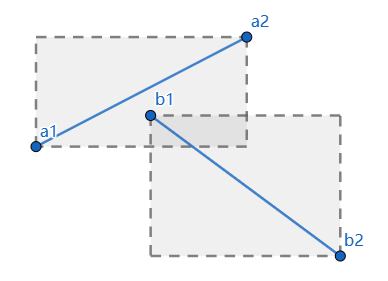
跨立实验
若两线段相交，则两线段必须跨立。就是：线段a1a2与线段b1b2相交，则a1和a2一定在线段b1b2的两侧。
2d向量叉乘v1×v2，结果>=0，v1旋转到v2角度在逆时针180度内；结果<=0，v1旋转到v2角度在顺时针180度内；
满足下面的1-1和1-2，或者满足2-1和2-2，就是跨立的（只需要用两条线段各自的1个端点，针对另一条线段做一次跨立，就可以判断出结果了。）
1-1) 线段b的端点b1对线段a做跨立
b1a1旋转到b1b2在逆时针180度内，b1a2旋转到b1b2在顺时针180度内，即(b1a1×b1b2)*(b1a2×b1b2) <= 0
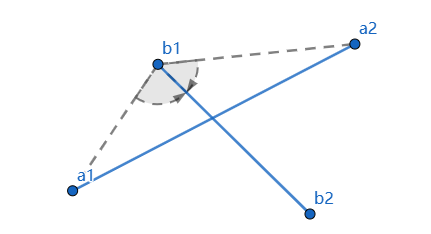
1-2) 线段a的端点a1对线段b做跨立
a1b1旋转到a1a2在顺时针180度内，a1b2旋转到a1a2在逆时针180度内，即(a1b1×a1a2)*(a1b2×a1a2)<=0
2-1) 线段b的端点b2对线段a做跨立
b2a2旋转到b2b1在逆时针180度内，b2a1旋转到b2b1在顺时针180度内，即(b2a2×b2b1)*(b2a1×b2b1)<=0
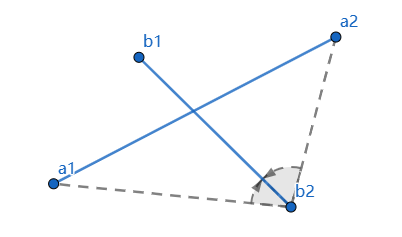
2-2) 线段a的端点a2对线段b做跨立
a2b1旋转到a2a1在逆时针180度内，a2b2旋转到a2a1在顺时针180度内，即(a2b1×a2a1)*(a2b2×a2a1)<=0
以下面2条不相交的线段为例，则不满足上面的4
public static bool IsTwoSegmentIntersect(Vector2 a1, Vector2 a2, Vector2 b1, Vector2 b2) { // 快速排斥：两个线段为对角线组成的矩形，如果这两个矩形没有重叠的部分，那么两条线段是不可能出现重叠的 if (Math.Max(a1.x, a2.x) < Math.Min(b1.x, b2.x)) return false; if (Math.Min(a1.x, a2.x) > Math.Max(b1.x, b2.x)) return false; if (Math.Max(a1.y, a2.y) < Math.Min(b1.y, b2.y)) return false; if (Math.Min(a1.y, a2.y) > Math.Max(b1.y, b2.y)) return false; // 跨立实验： // 如果两条线段相交，那么必须跨立，就是以一条线段为标准，另一条线段的两端点一定在这条线段的两段 // 也就是说a1 a2两点在线段b1 b2的两端，b1 b2两点在线段a1 a2的两端 double u = (a1.x - b1.x) * (b2.y - b1.y) - (b2.x - b1.x) * (a1.y - b1.y); //b1a1xb1b2 double v = (a2.x - b1.x) * (b2.y - b1.y) - (b2.x - b1.x) * (a2.y - b1.y); //b1a2xb1b2 if (u * v > 0.00000001) return false; double w = (b1.x - a1.x) * (a2.y - a1.y) - (a2.x - a1.x) * (b1.y - a1.y); //a1b1xa1a2 double z = (b2.x - a1.x) * (a2.y - a1.y) - (a2.x - a1.x) * (b2.y - a1.y); //a1b2xa1a2 if (w * z > 0.00000001) return false; return true; }
参考
GIS算法：1_两点线段是否相交 - 知乎 (zhihu.com)
