BZOJ3670 [Noi2014]动物园[KMP]
这是noi题吗。。为什么我这种菜鸡都会做。。表示质疑。
求一个串$S$的每一个前缀$i$的不重叠的既为前缀又为后缀(下简称:border)的子串数量$num$。
模仿KMP,假设当前在求$i$的$next$数组,同时希望求出$num$,那也就是看前缀$i-1$中是border且不重叠的所有子串和第$i$位的匹配数量。
那么可以从最长的一个不超过$\lfloor i/2 \rfloor$的border开始比对,可以匹配就$++num$,然后继续跳(也就是$k=next[k]$)。
这里类似于KMP的自匹配,只不过将$j$要求为不超过串长一半$k$来匹配。
看了$N \leq 1000000$,应当是线性的,尝试寻找递推方法。
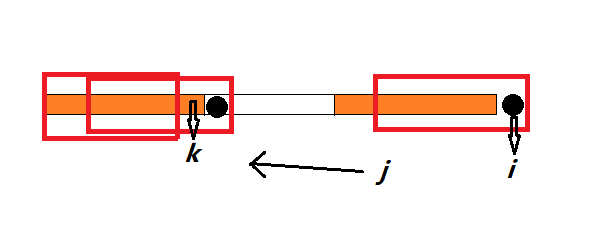
自己瞎画了个图。现在期望寻找递推关系。橙色是不超过$\lfloor i/2 \rfloor$的能成功匹配的border。
$k$是不超过串长一半的最长border,$j$是最长border(无限制,就是原KMP的)
发现图中三个红色框框柱的串都是等价的。这意味着我如果要求:有多少个像图中一样最左最右两个红框相等的。
通过上述转化,发现就是要求前缀$k+1$里面有多少可重叠的border。设之为$g[k+1]$。
那么$num=g[k+1]$。于是就成功了。
下面看怎么推$g[i]$。发现最长border$j$的$g[j]$有多少相等的子border,$g[i]$就有多少,还要再加上本身全串的一个$1$。可以用类似上面那个图的方法来等价。
于是就做一次KMP,每匹配一位时候同时让$j$和$k$跳$next$至满足要求,并进行匹配和递推。详见code。

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #define dbg(x) cerr << #x << " = " << x <<endl 7 using namespace std; 8 typedef long long ll; 9 typedef double db; 10 typedef pair<int,int> pii; 11 template<typename T>inline T _min(T A,T B){return A<B?A:B;} 12 template<typename T>inline T _max(T A,T B){return A>B?A:B;} 13 template<typename T>inline char MIN(T&A,T B){return A>B?(A=B,1):0;} 14 template<typename T>inline char MAX(T&A,T B){return A<B?(A=B,1):0;} 15 template<typename T>inline void _swap(T&A,T&B){A^=B^=A^=B;} 16 template<typename T>inline T read(T&x){ 17 x=0;int f=0;char c;while(!isdigit(c=getchar()))if(c=='-')f=1; 18 while(isdigit(c))x=x*10+(c&15),c=getchar();return f?x=-x:x; 19 } 20 const int N=1e6+7,P=1e9+7; 21 char s[N]; 22 int nxt[N],f[N],g[N]; 23 int T,ans; 24 25 int main(){//freopen("1.in","r",stdin);freopen("1.ans","w",stdout); 26 read(T);while(T--){ 27 scanf("%s",s+1); 28 nxt[1]=f[1]=0;ans=g[1]=1; 29 int j=0,k=0,n=strlen(s+1); 30 for(register int i=2;i<=n;++i){ 31 while(j&&s[i]^s[j+1])j=nxt[j]; 32 while(k&&(s[i]^s[k+1]||k>=(i>>1)))k=nxt[k]; 33 nxt[i]=s[i]==s[j+1]?++j:0; 34 (s[i]==s[k+1])&&(++k); 35 f[i]=g[k]; 36 g[i]=g[j]+1; 37 ans=ans*1ll*(f[i]+1)%P; 38 // dbg(i),dbg(j),dbg(k),dbg(f[i]); 39 } 40 printf("%d\n",ans); 41 } 42 return 0; 43 }


