【BZOJ3047&2125】Freda的传呼机
Description
为了 随时 与 rainbow快速交流, Freda制造了 两部传呼机 。Freda和 rainbow所在的地方有N座房屋、M条双向 光缆 。每条光缆连接两座房屋, 传呼机发出的信号只能沿着光缆传递,并且 传呼机的信号 从光缆的其中一端传递到另需要花费 t单位时间 。现在 Freda要 进行 Q次试验, 每次选取两座房屋,并想知道 传呼机的信号在这两座房屋之间传递 至少需 要多长时间。 Freda 和 rainbow简直弱爆了有木有T_TT_T ,请你帮他们吧……
N座房屋 通过光缆 一定是连通的, 并且这 M条光缆有以下三类连接情况:
A:光缆不形成环 ,也就是光缆仅 有 N-1条。(30%的数据)
B:光缆只 形成一个环,也就是光缆 仅有 N条。(50%的数据)
C:每条光缆仅在一个环中。(10%数据N,M较小,10%数据N,M较大)
Solution
先看A类数据,显然树上 lca 可以完美解决。
再看一下B类数据,环套树,我们考虑拆掉环。
搜索一遍把环边找出来,特殊处理环边连接的两个点到所求两点的距离即可。
对于C类数据,仙人掌图。
于是我们可以考虑将环拆散,对于每个环,我们找出它们的环顶(这里环顶的定义是进入该环必须经过的点,注意,环顶不属于任何环,因为它可以被多个环包含),然后把环顶向这个环上的点连一条边,边权为该点到环顶的最短路。
具体实现就是开个栈,处理每个环上的点经过环的两条路径的距离即可。
然后原图就变成一棵树了,是不是觉得很简单了!
然而,如果我们直接像A类数据那样的话,会出现一个问题:
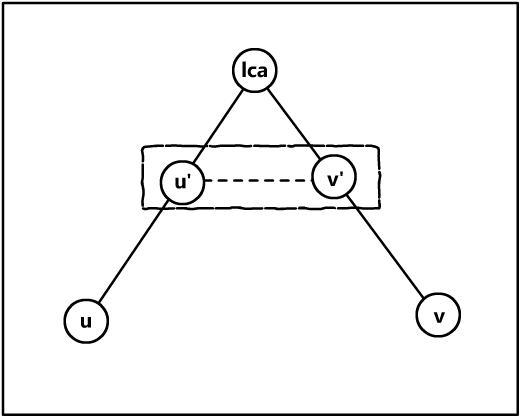
我们看,如果
(u′,v′)
在同一个环内,那么它们的最短距离就可能不需要经过
lca
,那么统计的时候答案就可能大了。
这时,我们先前统计的环上的两条路径就派上用场了。
记两条路径分别为
l1
,
l2
,那么这两个点的最短路就是:
min(l1x+l2y,l2x+l1y,|l1x−l1y|)
(
|a|
表示
a
的绝对值)
所以,我们求
注意细节。
Code
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#define fo(i,j,k) for(int i=j;i<=k;i++)
#define fd(i,j,k) for(int i=j;i>=k;i--)
#define N 20010
#define M 40010
using namespace std;
int to[M],next[M],last[M],val[M],num=0;
int nt[M],nn[M],nl[M],nv[M],cnt=0;
int dfn[N];
int top=0;
int f[N][15],g[N][15];
int fa[N];
int c1[N],c2[N];
int bl[N],zx[N];
int zz=0;
int d[N];
struct stack{
int x,s;
}st[N];
int tt=0;
int abs(int x)
{
return x<0?-x:x;
}
void link(int x,int y,int c)
{
num++;
to[num]=y;
next[num]=last[x];
last[x]=num;
val[num]=c;
}
void nlink(int x,int y,int c)
{
cnt++;
nt[cnt]=y;
nn[cnt]=nl[x];
nl[x]=cnt;
nv[cnt]=c;
}
void dfs(int x)
{
dfn[x]=++tt;
for(int i=last[x];i;i=next[i])
{
int v=to[i];
if(v!=fa[x] && !dfn[v])
{
fa[v]=x;
top++;
st[top].x=v;
st[top].s=val[i];
dfs(v);
}
else if(v!=fa[x] && dfn[v]<dfn[x])
{
zz++;
int p=top,tmp=val[i];
while(st[p].x!=v && p)
{
c1[st[p].x]=tmp;
tmp+=st[p].s;
p--;
}
tmp=st[p+1].s;
fo(i,p+1,top)
{
zx[st[i].x]=v;
bl[st[i].x]=zz;
c2[st[i].x]=tmp;
int jx=min(c1[st[i].x],c2[st[i].x]);
nlink(st[i].x,v,jx);
nlink(v,st[i].x,jx);
tmp+=st[i+1].s;
}
}
}
top--;
}
bool vis[N];
void cxlb(int x)
{
vis[x]=true;
for(int i=last[x];i;i=next[i])
{
int v=to[i];
if(v!=fa[x] && !vis[v])
{
if((bl[x]!=bl[v] || !bl[x] && !bl[v]) && zx[v]!=x && zx[x]!=v)
{
nlink(x,v,val[i]);
nlink(v,x,val[i]);
}
cxlb(v);
}
}
}
int sbll=0;
void find(int x)
{
for(int i=nl[x];i;i=nn[i])
{
int v=nt[i];
if(v!=f[x][0])
{
f[v][0]=x;
g[v][0]=nv[i];
d[v]=d[x]+1;
find(v);
}
}
}
int lca(int x,int y)
{
int tmp=0;
if(d[x]>d[y]) swap(x,y);
fd(i,14,0)
while(d[f[y][i]]>=d[x])
tmp+=g[y][i],y=f[y][i];
if(x==y) return tmp;
fd(i,14,0)
while(f[x][i]!=f[y][i])
{
tmp+=g[x][i]+g[y][i];
x=f[x][i];
y=f[y][i];
}
if(x!=y && bl[x] && bl[x]==bl[y]) tmp+=min(min(c1[x]+c2[y],c1[y]+c2[x]),min(abs(c2[x]-c2[y]),abs(c1[x]-c1[y])));
else tmp+=g[x][0]+g[y][0];
return tmp;
}
int main()
{
int n,m,q;
cin>>n>>m>>q;
fo(i,1,m)
{
int x,y,t;
scanf("%d %d %d",&x,&y,&t);
link(x,y,t);
link(y,x,t);
}
dfs(1);
cxlb(1);
find(1);
d[0]=-1;
fo(j,1,14)
fo(i,1,n)
{
f[i][j]=f[f[i][j-1]][j-1];
g[i][j]=g[i][j-1]+g[f[i][j-1]][j-1];
}
fo(i,1,q)
{
int x,y;
scanf("%d %d",&x,&y);
printf("%d\n",lca(x,y));
}
}


