【题解】洛谷：P8593 「KDOI-02」一个弹的投

P8593 「KDOI-02」一个弹的投

物理题。

首先你要搞懂什么时候会炮弹碰撞，结论：y坐标相同时，水平位置 \(x_i\le x_j\) 且落点满足 \(d_i\ge d_j\)，两炮弹必然碰撞。

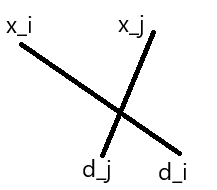
但是为什么呢，像我这种完全没学高中物理的伪高中生就不会了，下落时每个物体的相对的高度差是不变的，因为根据伽利略运动独立性原理，平抛运动的竖直方向运动仅由重力加速度 \(g\) 决定，与物体的初始水平速度无关。

所以只有高度相同时下落才有可以碰撞，上面那个图就是抽象出来的函数图像，我们就像有一条平行于x轴的线从上向下移动，交点就是他们碰撞点。

那学会了物理后这题就很简单了，碰撞成立条件其实就是逆序对条件，我们就可以将问题转化为求每个点的逆序对个数，我们对于每一个横坐标相同的点集，按照纵坐标排序，用落点纵坐标求逆序对，注意要离散化。

但是还有第二个子问题，用装置减弱爆炸，用贪心！每个点可以减少的威力为 \(\min{\{p_i,a_i\}}\)，我们将这个储存下来按照从大到小排序，然后在从总和中减去即可 \(\sum_{i=1}^n p_i -\sum_{j=1}^m a_i\)。

#include <bits/stdc++.h>
#define int long long
#define ls p<<1
#define rs p<<1|1 
#define re register 
const int N=5e5+10;
const int mod=998244353;
using namespace std;
 
int n,m;
 
double b[N<<3];
int f[N];
struct ss{
	int x,y,id;
	double d;
}a[N];
 
int c[N];
int tot;
int t[N<<3];
 
bool cmp(ss g,ss h){
	if(g.y==h.y){
		return g.x<h.x;
	}
	return g.y<h.y;
}
 
int lb(int x){
	return x&-x;
}
 
void change(int x,int k){
	while(x<=tot){
		t[x]+=k;
		x+=lb(x);
	}
}
 
int query(int x){
	int sum=0;
	while(x){
		sum+=t[x];
		x-=lb(x);
	}
	return sum;
}
 
bool cmp2(ss g,ss h){
	return g.id<h.id;
}
 
signed main(){
//	freopen("missile4.in","r",stdin);
//	freopen("a.out","w",stdout);
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 
	cin>>n>>m;
	
	int o=0;
	
	for(int i=1;i<=n;i++){
		int v;
		cin>>a[i].x>>a[i].y>>v;
		a[i].id=i;
		a[i].d=a[i].x+v*sqrt(2.0*a[i].y/9.8); 
		b[++o]=a[i].x;
		b[++o]=a[i].y;
		b[++o]=a[i].d;
	}
	
	sort(b+1,b+1+o);
	tot=unique(b+1,b+o+1)-b-1; 
	
	sort(a+1,a+n+1,cmp);
	
	for(int i=1;i<=n;i++){
		int r=n;
		int pos;
		for(int j=i;j<=n;j++){
			if(a[j].y!=a[j-1].y&&j!=i){
				r=j-1;
				break;
			}
			pos=lower_bound(b+1,b+tot+1,a[j].d)-b;
			c[a[j].id]+=query(tot)-query(pos-1);
			change(pos,1);	
		}
		for(int j=1;j<=tot;j++){
			t[j]=0;
		}
		for(int j=r;j>=i;j--){
			pos=lower_bound(b+1,b+tot+1,a[j].d)-b;
			c[a[j].id]+=query(pos);
			change(pos,1);	
		}
		for(int j=1;j<=tot;j++){
			t[j]=0;
		}
		i=r;
	}
	sort(a+1,a+1+n,cmp2);
	int ans=0;
	for(int i=1;i<=n;i++){
		int x;
		cin>>x;
		ans+=c[i];
		f[i]=min(c[i],x);
	} 
	sort(f+1,f+1+n);
	for(int i=n;i>=n-m+1;i--){
		ans-=f[i];
	}
	cout<<ans;
	return 0;
}