好的难题（目前收录的确实很难）
[ARC073F] Many Moves
非常厉害的一题，暴力做法枚举当前两颗棋子的位置，再枚举上一次操作时的两颗棋子位置来转移，这样复杂度为 \(O(qn^4)\)，非常糟糕。
因为转移时总有一个棋子在 \(x_i\) 的位置，所有我们可以设状态为 \(f_{i,j}\) 为经过了前 \(i\) 个位置，当前不在 \(x_i\) 位置上的那个棋子在 \(j\) 位置上的最小花费，我们进行分类讨论。
当 \(j\neq x_{i-1}\) 时，说明 \(j\) 这颗棋子上次也没有移动，所以 \(x_i\) 是由 \(x_{i-1}\) 转移过来的，于是又 \(f_{i-1,j}+\left| x_i-x_{i-1} \right|\)。
当 \(j=x_{i-1}\) 时，此时我们就要枚举 \(k\) 找到最小的到 \(x_i\) 的距离花费，于是有 \(\min {(f_{i-1,k}+\left| x_i-k \right|)}\)，我们分类讨论这个 \(k\) 的值来去掉这个绝对值，当 \(k\ge x_i\) 有 \(\min{(f_{i-1,k}+k-x_i)}\)，当 \(k\le x_i\) 有 \(\min{(f_{i-1,k}-x_i+k)}\)。
于是我们就可以用线段树分别维护 \(f_{k}+k\) 和 \(f_{k}-k\) 即可。
因为 \(f_{i,k}\) 只与 \(f_{i-1,k}\) 有关，所以直接用线段树进行区间查询区间修改来滚动数组即可。
W - Intervals
这题也很厉害，也有点套路的，和上一题一样都需要用线段树。
对于区间操作，我们对右端点排序这样可以不漏地全部判断，可以抽象为一条 01 串，我们通过枚举右端点 \(i\)，向前枚举上一次选择为1的位置 \(j\)，所有线段右端点为 \(i\)，左端点小于等于 \(j\) 的线段的权值都可以选择，于是我们有 \(f[i][j]=f[i-1][j]+\sum_{l_x\le j,r_x=i} v_x,j<i\)。
当我们 \(j=i\) 时，那前 \(i-1\) 个位置上一次选择为 \(1\) 的位置可以是任意位置，所有取最大值即可，于是我们有 \(f[i][i]=\max_{j=1}^{i-1}{f[i-1][j]}\)。
但是这样复杂度还是不够，考虑优化，如果我们统一加上所有相同右端点的线段更新之前被包含的每个点的状态，并每次取之前点的最大值转移到我们当前点的状态的话，这就是一个线段树最大值和区间加操作，好好好又是一个线段树优化dp，我哪辈子能会啊！！！
D - Median Pyramid Hard
我们考虑如果是个 01 串的话最上面会是什么样的，如 0 1 1 0 1 向上传递为 1 1 1 ，感觉是不是有点感觉了，如果两个相邻相同会一直向上传递：
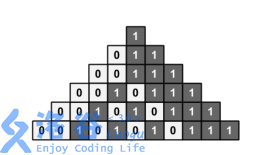
因为中位数的原因所以我们靠取中间的相邻的相同数，但是我们知道这个有什么用呢，这题又不是这样的，我们可以转化思想，二分答案，比他大的为 \(1\)，反之为 \(0\)，然后再判断并不断缩小边界，最后就只会确定一个唯一的值。
P8867 [NOIP2022] 建造军营
倒也不是特别难，但是能场切确实厉害。
看到断边后不连通想到割边，那没割边的边双连通分量就可以缩点，到这确实都是模板，接下来树形 dp。
我们设状态为 \(f_{x,0/1}\)，其中 \(f_{x,1}\) 为仅仅只有 \(x\) 这颗子树有军营建造的方案数并且所有军营路径上的边都选的方案数，\(f_{x,0}\) 为 \(x\) 这颗子树完全没有军营的方案数，缩到同一点的选点方案可以随意搭配，于是我们有 \(f_{x,0}=1\) 和 \(f_{x,1}=2^{siz_x}-1\)。
于是我们有一下转移：
到 \(y\) 这颗子树没有军营，\(x\) 之前的子树也没有军营，连接 \(y\) 的边可选可不选：
到 \(y\) 这颗子树没有军营，\(x\) 之前的子树有军营，连接 \(y\) 的边可选可不选：
到 \(y\) 这颗子树有军营，\(x\) 之前的子树没有军营，连接 \(y\) 的边必须选：
到 \(y\) 这颗子树有军营，\(x\) 之前的子树有军营，连接 \(y\) 的边必须选：
统计答案的话肯定是除了这颗子树军营必选边外的其他所有的边都可以随便选，但是父边不能选（选的话就统计到父节点了，会重复），父节点没父边所以要格外统计。
\(2\) 的幂次要预处理不然炸飞你。
