GSS系列
SPOJ 的数据结构的专题训练,没事写一下题解。
GSS1 - Can you answer these queries I
没有修改哦,考虑如何求最大子段和。
可以想到大区间的最大子段和可以分为三种情况,只在左,只在右,在中间横跨左右区间,在中间的怎么求呢,可以发现区间和可以是左区间的最大后缀和和右区间的最大前缀和的和,接下来取个最大值就好了。
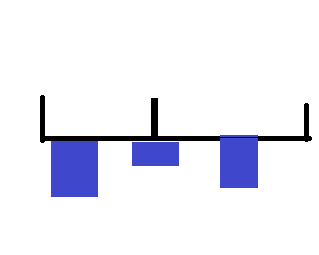
那么我们就要想如何求最大前缀和了,大区间的最大前缀和的右端点可以不超过中间也可以超过中间,前者直接用左儿子区间的最大前缀和,后者用左区间总和加上右区间的最大前缀和即可,此时取最大值赋值即可,最大后缀和同样方法求就可以了。
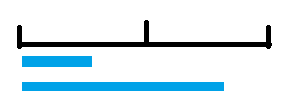
此时我们明确了要维护区间的最大子段和、最大前缀和、最大后缀和、区间总和,然后 do it!!!。
我相信你可以的
#include<bits/stdc++.h>
#define ll long long
#define ls (p<<1)
#define rs (p<<1|1)
using namespace std;
#define int ll
const int N=3e5+10;
int n,m,q;
int w[N];
inline int read(){
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct ss{
int sum,lmax,rmax,mx;
}a[N];
void pushup(int p){
a[p].lmax=max(a[ls].lmax,a[ls].sum+a[rs].lmax);
a[p].rmax=max(a[rs].rmax,a[rs].sum+a[ls].rmax);
a[p].sum=a[ls].sum+a[rs].sum;
a[p].mx=max(a[ls].rmax+a[rs].lmax,max(a[ls].mx,a[rs].mx));
}
void build(int p,int l,int r){
if(l==r){
a[p].lmax=a[p].rmax=a[p].sum=a[p].mx=w[l];
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(p);
}
ss query(int p,int pl,int pr,int l,int r){
if(pl>=l&&pr<=r){
return a[p];
}
int mid=(pl+pr)>>1;
if(l>mid){
return query(rs,mid+1,pr,l,r);
}
if(r<=mid){
return query(ls,pl,mid,l,r);
}
ss ans,x,y;
x=query(ls,pl,mid,l,r);
y=query(rs,mid+1,pr,l,r);
ans.lmax=max(x.lmax,x.sum+y.lmax);
ans.rmax=max(y.rmax,y.sum+x.rmax);
ans.sum=x.sum+y.sum;
ans.mx=max(x.rmax+y.lmax,max(x.mx,y.mx));
return ans;
}
signed main(){
ios::sync_with_stdio(false);
n=read();
for(int i=1;i<=n;i++){
w[i]=read();
}
build(1,1,n);
m=read();
for(int i=1;i<=m;i++){
int l,r;
l=read(),r=read();
cout<<query(1,1,n,l,r).mx<<"\n";
}
return 0;
}
GSS3 - Can you answer these queries III
这就是 GSS1 加了个修改操作没什么好说的,就简单加上就可以了。
这你也要看???我看你真是饿了
#include<bits/stdc++.h>
#define ll long long
#define ls (p<<1)
#define rs (p<<1|1)
using namespace std;
#define int ll
const int N=5e5+10;
int n,m,q;
int w[N];
inline int read(){
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
struct ss{
int sum,lmax,rmax,mx;
}a[N];
void pushup(int p){
a[p].lmax=max(a[ls].lmax,a[ls].sum+a[rs].lmax);
a[p].rmax=max(a[rs].rmax,a[rs].sum+a[ls].rmax);
a[p].sum=a[ls].sum+a[rs].sum;
a[p].mx=max(a[ls].rmax+a[rs].lmax,max(a[ls].mx,a[rs].mx));
}
void build(int p,int l,int r){
if(l==r){
a[p].lmax=a[p].rmax=a[p].sum=a[p].mx=w[l];
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(p);
}
void change(int p,int pl,int pr,int pos,int k){
if(pl==pr){
a[p].lmax=a[p].rmax=a[p].sum=a[p].mx=k;
return;
}
int mid=(pl+pr)>>1;
if(pos<=mid){
change(ls,pl,mid,pos,k);
}
else{
change(rs,mid+1,pr,pos,k);
}
pushup(p);
}
ss query(int p,int pl,int pr,int l,int r){
if(pl>=l&&pr<=r){
return a[p];
}
int mid=(pl+pr)>>1;
if(l>mid){
return query(rs,mid+1,pr,l,r);
}
if(r<=mid){
return query(ls,pl,mid,l,r);
}
ss ans,x,y;
x=query(ls,pl,mid,l,r);
y=query(rs,mid+1,pr,l,r);
ans.lmax=max(x.lmax,x.sum+y.lmax);
ans.rmax=max(y.rmax,y.sum+x.rmax);
ans.sum=x.sum+y.sum;
ans.mx=max(x.rmax+y.lmax,max(x.mx,y.mx));
return ans;
}
signed main(){
ios::sync_with_stdio(false);
n=read();
for(int i=1;i<=n;i++){
w[i]=read();
}
build(1,1,n);
m=read();
for(int i=1;i<=m;i++){
int op,l,r;
op=read(),l=read(),r=read();
if(op==0){
change(1,1,n,l,r);
}
else{
cout<<query(1,1,n,l,r).mx<<"\n";
}
}
return 0;
}
GSS4 - Can you answer these queries IV
某某双倍经验,因为开方有个性质,开方大约6次后就必定为1,当区间最大值不大于1时,那这次操作就没有意义,不执行操作,有了这个剪枝后你就可以直接暴力修改了。
这么简单的思路也要看代码???
#include<bits/stdc++.h>
#define ll long long
#define ls (p<<1)
#define rs (p<<1|1)
using namespace std;
#define int ll
const int N=5e5+10;
int n,m,q;
int w[N];
int sum[N],mx[N];
inline int read(){
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void build(int p,int l,int r){
if(l==r){
sum[p]=w[l];
mx[p]=w[l];
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
sum[p]=sum[ls]+sum[rs];
mx[p]=max(mx[ls],mx[rs]);
}
void change(int p,int pl,int pr,int l,int r){
if(mx[p]<=1){
return;
}
if(pl==pr){
sum[p]=sqrt(sum[p]);
mx[p]=sqrt(mx[p]);
return;
}
int mid=(pl+pr)>>1;
if(l<=mid&&mx[ls]>1){
change(ls,pl,mid,l,r);
}
if(mid<r&&mx[rs]>1){
change(rs,mid+1,pr,l,r);
}
sum[p]=sum[ls]+sum[rs];
mx[p]=max(mx[ls],mx[rs]);
if(mx[p]<=1){
return;
}
}
int query(int p,int pl,int pr,int l,int r){
int ans=0;
if(pl>r||pr<l){
return 0;
}
if(pl>=l&&pr<=r){
return sum[p];
}
int mid=(pl+pr)>>1;
ans+=query(ls,pl,mid,l,r);
ans+=query(rs,mid+1,pr,l,r);
return ans;
}
signed main(){
// ios::sync_with_stdio(false);
int cnt=0;
while((scanf("%lld",&n))!=EOF){
printf("Case #%d:\n",++cnt);
for(int i=1;i<=n;i++){
w[i]=read();
}
build(1,1,n);
cin>>m;
for(int i=1;i<=m;i++){
int op;
int u,v;
op=read();
u=read();
v=read();
if(u>v){
swap(u,v);
}
if(op==1){
printf("%lld\n",query(1,1,n,u,v));
}
else{
change(1,1,n,u,v);
}
}
printf("\n");
memset(sum,0,sizeof sum);
memset(mx,0,sizeof mx);
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号