【算法学习】笛卡尔树

合集 - 【算法学习】(35)

1.【算法学习】排序2024-08-272.【算法学习】Manacher 马拉车2024-08-293.【算法学习】KMP 算法2024-09-014.LCA 最近公共祖先（树链和倍增）这次真有树链了！！！2024-08-305.线段覆盖问题2024-08-296.【算法学习】学换根dp有感2024-09-207.二分图最大匹配2024-09-178.【算法学习】01BFS2024-09-179.洛谷 P1892 [BOI2003] 团伙 种类并查集 扩展域并查集2024-09-1110.【算法学习】高斯消元法2024-09-1011.贝叶斯公式2024-09-0712.背包2024-09-0513.【算法学习】模拟退火2024-09-0514.【算法学习】基环树2024-10-2915.【算法学习】树链部分2024-10-2916.【算法学习】莫队2024-10-2917.【算法学习】分块九讲2024-10-2818.平衡树2024-10-2319.圆方树2024-10-2220.【算法学习】点分治2024-10-1121.公式2024-10-09

22.【算法学习】笛卡尔树2024-10-04

23.【算法学习】悬线法2024-10-0424.欧几里得算法与 EX2024-09-2325.【算法学习】逆元与求解2024-09-2326.【算法学习】费马定理2024-09-2327.三分2024-09-2328.裴蜀定理2024-09-2329.【算法学习】欧拉函数φ2024-09-2330.【算法学习】二维转一维问题2024-11-0331.【算法学习】扫描线2024-11-0132.【算法学习】矩阵乘法2024-10-3133.【算法学习】同余最短路2024-11-0434.【算法学习】组合数学2024-11-0535.【算法学习】反悔贪心2024-11-06

收起

前言

oi-wiki 已讲的足够清晰

顺着思路看下去还是很简单的，我只列出代码展示。

我现在肯定不会这么说了，虽然考这个的概率还是很小但还是要记录的（学习是给自己学的，笔记是给自己记的）

笛卡尔树要满足堆和二叉搜索树的两个性质，而且他有两种键值 \(w,k\)，分别是根节点大于子节点，左节点小于根节点，根节点小于右节点。

竞赛中使用笛卡尔树时，常用数组下标作为二元组的键值 \(k\)。

真的讲解

我们将使用栈构建树，我们始终维护一条右链，当插入一个点，在链上找到第一个w小于该节点的节点，将该节点的右子树接在新点的左子树上，新点成为新右链的最后一个点，过程正如 oi-wiki 一样。

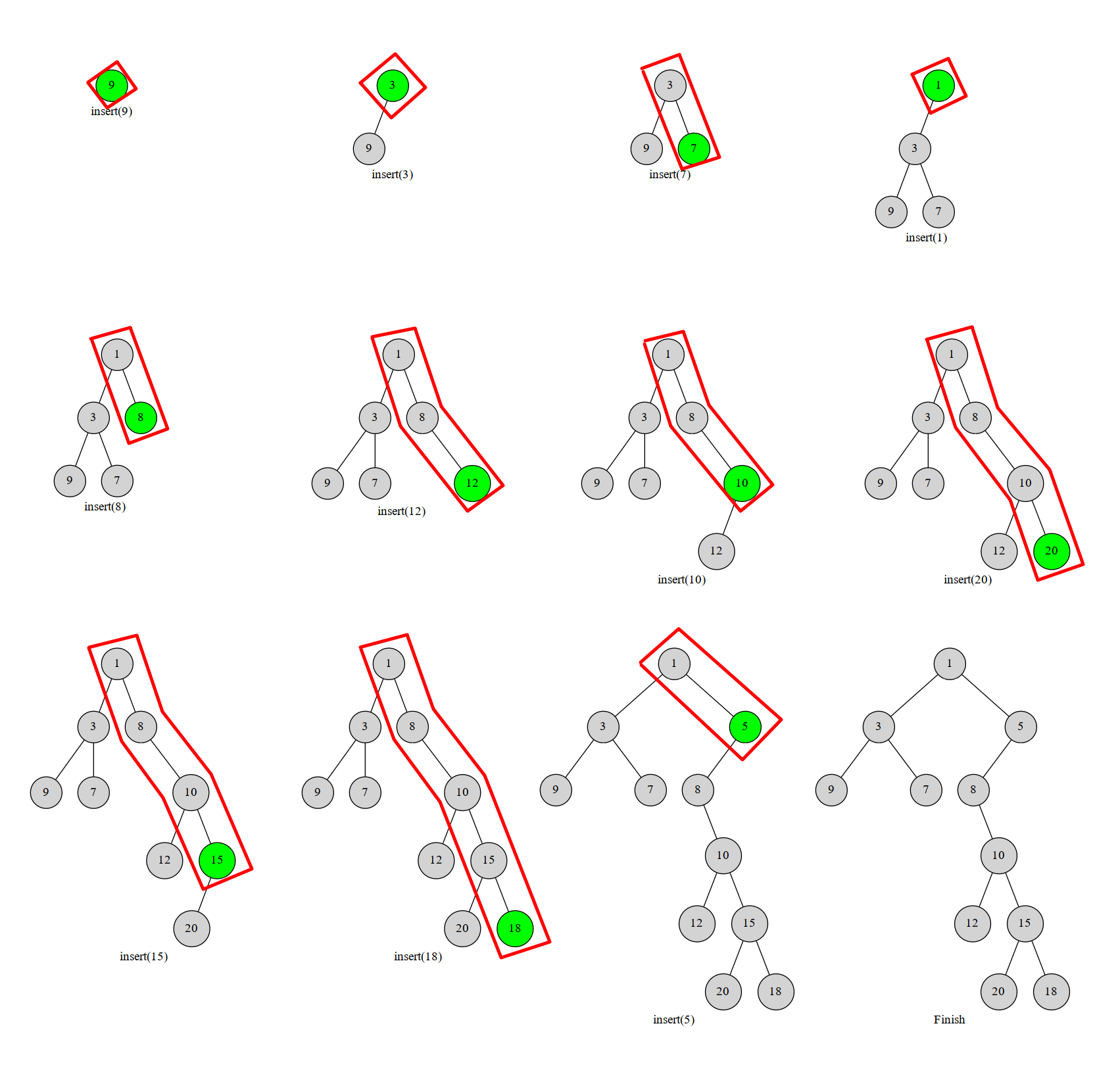
然后上代码，感觉比 wiki 还简单明显。

s[1]=1;
int top=1;
for(int i=2;i<=n;i++){
    while(a[s[top]]>a[i]&&top){
    	top--;
	}
	if(!top){
		l[i]=s[top+1];
	}
	else{
		l[i]=r[s[top]];
		r[s[top]]=i;
	}
	s[++top]=i;
}

题目练习

P5854 【模板】笛卡尔树

就是一个板子，按上面说的写就可以，我就不出代码你能怎样，自己写！！！

P1377 [TJOI2011] 树的序

这题需要读懂题意才可以，发现就是个构造笛卡尔树的题，但是好像又不是模板题，怎么办，我们将序列排序使得字典序最小，然后我们按照位置id加点使得不破坏树的插入顺序，每次加入点和笛卡尔树一样放左接右，因为我们是按id加点，所以应该早加的终究会在上方，只不过在过程中使得能在上方加在左子树的尽量在上。

点击查看代码

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+10;
#define int ll
int n;
int l[N];
int r[N];
int s[N];
struct ss{
	int a,id;
}a[N];
void dfs(int x){
	if(x==0){
		return;
	} 
	cout<<a[x].a<<" ";
	dfs(l[x]);
	dfs(r[x]);
}
bool cmp(ss g,ss h){
	return g.a<h.a;
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n;
    for(int i=1;i<=n;i++){
    	cin>>a[i].a;
		a[i].id=i;
	}
	sort(a+1,a+n+1,cmp);
    int top=0;
    for(int i=1;i<=n;i++){
    	while(a[s[top]].id>a[i].id&&top){
    		top--;
		}
		l[i]=r[s[top]];
		r[s[top]]=i;
		s[++top]=i;
	}
	dfs(r[0]);
    return 0;
}