动态规划专项训练 1
前言
RT，因为我dp实在是太差了，我将集中进行动态规划的专项训练，按照下方题单，依次写下题解，好进行复习分析，可能还会夹杂其他题，但不重要了。
24/9/29 有感，我发现部分题从状态开始就有点难想了，转移相对来说还较容易些，以及还要在转移时多去考虑细节性的问题，虽然我已经做了这么多，但是我觉得好像遇到题还是没思路，菜就多练吧。
24/10/17 有感，我发现像状压dp和区间dp都有点套路的，一点一点想是可以的，还有dp的奥义其实是先想暴力做法再做优化的，像什么单调队列优化，树状数组优化都是先有暴力再发现中间转移有性质就优化掉了。
注：我写的内容基本只是为了整理给自己看的，就只是顺个思路，看详细代码还是取题解第一个里面看吧（第一个确实都挺不错的）
简单dp入门题
Knapsack 2
我是唐完了，我就学了个不知所以然的01背包就随便了，但遇到这题还是不会，可以发现这题重量非常大，所以不能枚举重量了，此时我们枚举价格，找到最大的满足重量的价值，就是01背包反了过来。
总结：看数据范围做题有奇效。
P1359 租用游艇
严格来说是图论最短路题但可以用 dp 做，首先你需要看懂题（不会就我看不懂吧），然后可以正向递推：加边时更新最小距离，也可以反向推：从终点向上更新（好像都一样）。
P1802 5 倍经验日
变形 01 背包，分类讨论。
当 \(j>=w[i]\) 有 \(max(dp[j]+a[i],dp[j-w[i]]+b[i])\)。
当 \(j<w[i]\) 必定打不过，那就拿点经验就跑吧，有 \(dp[j]+=a[i]\)。
P1095 守望者的逃离
有贪心和dp两种做法：
-
贪心：分别计算 只闪现 与 只跑步 的距离，如果闪现大于跑步，就可以将跑步距离更换为闪现的距离，这样就相当于在合适的时候进行闪现否则就跑步的操作。
-
dp：先递推求出 只闪现 的距离数组，再进行一遍 只跑步 的操作，但只跑步大于只闪现，将这步替换为跑步，同样实现相同操作结果。
P1507 NASA的食物计划
改版 01 背包，状态多加一位，多枚举一重即可。
P1077 摆花
其实还是要先看懂题意，要连续选多相同编号盆，最后选 \(m\) 个盆，问方案数，设状态为 \(dp[i][j]\) 选前 \(i\) 种盆，选择了 \(j\) 个盆的方案数，此时可以得到朴素的转移，但发现这与 01 背包有点像，每种盆选的数量可以抽象为物品的体积，那没得说，直接套板去吧。
P3842 线段
设状态为 \(dp[i][0]\) 为走完第 \(i\) 行停到线段左端点所用的最短的长度，相反 \(dp[i][1]\) 为走完第 \(i\) 行停到线段右端点所用的最短的长度。
可以发现本行想要停到左端点并走完本行线段要上一行的左端点到本行右端点再到左端点或上一行右端点到本行右端点再到左端点，如下图（有点抽象但就是这样）。
P1541 乌龟棋
设成状态为 \(f[a][b][c][d]\) 为选 \(a\) 张 \(1\) 牌、\(b\) 张 \(2\) 牌、\(c\) 张 \(3\) 牌、\(d\) 张 \(4\) 牌可得到最大分数。
这时分别枚举 \(a,b,c,d\) 就成了多重背包问题了。
P1064 金明的预算方案
01 背包的变种，因为最多只有2个附件，所以可以分为5种情况：
-
只拿主件
-
不拿主件
-
拿主和附1
-
拿主和附2
-
拿主和附1、2
记得判断容量，然后其他正常递推即可了（确实是个板子，但是你要想到状态）。
P2170 选学霸
题意是实力相当的学霸们只能都选和都不选，所以我们可以用并查集统计连通块内的人数，然后 01 背包地进行选人，因为可以大于 \(m\)，所以容量为 \(2m\)，最后我们找到距离m最近的最小的价值。
P1387 最大正方形
要求左右和左上都是1，所以对他们取个min，就可以保证如果想组成正方形要他们都大于1才可以。
P1681 最大正方形II
要求颜色相反，所以状态多一维，转移也用相反的颜色状态转移。
P2340 [USACO03FALL] Cow Exhibition G
01背包板子题，但是可能会出现负数，所以下标要有增移量，而且注意体积是负数是，减会增加，所以要正着遍历。
P4310 绝世好题
他仅仅要求序列最长的长度，我们可以引用最长上升子序列的思想（有些隐蔽），设状态 \(dp[i]\) 为二进制第 i 位为 1 的最长序列长度，对于一个数 10101 \(dp[1],dp[3],dp[5]\) 都应该加一，对他们的位的长度取个最大值，答案取最大值就好了。
P1868 饥饿的奶牛
入机的我想不到，还是太菜了，其实需要按照尾位置小于现在位置的头位置的最大的价值，所以我们开始考虑优化，按尾位置排序，二分查找即可。
P1941 [NOIP2014 提高组] 飞扬的小鸟
写的差不多了，发现不能用一维背包，然后开摆看题解，发现还有一些细节没注意，但最后也是A了，发现我的水平确实进步了！！
把每个位置的上升看作完全背包问题，把下降看为01背包问题就好了，有水管的位置都清为最大值使之后无法通过管道转移，水管中间空出来使得只能通过这转移。然后就是一些细节转移了，要用二维滚动数组小小优化。
P2736 [USACO3.4] “破锣摇滚”乐队 Raucous Rockers
很常规的二维 dp 题，我们发现我们需要知道物品和唱片和唱片容量，所以我们有三重循环，然后我们就可以设 \(f_{i,j}\) 为选用了 \(i\) 个唱片，当前唱片用的容量为 \(j\) 的最多歌曲数。
于是我们有以下转移：
\(f_{i,j}=\max \{{f_{i,j},f_{i,j-a}+1,f_{i-1,j}+1}\}\) 分别为不选这个音乐、唱片容量够用则选择这个音乐、开一个新的唱片放音乐。
P1944 最长括号匹配
题意dp题，要求是连续的合法括号，也是要推出式子就可以了，f[i] 以i结尾最长的合法序列长度，然后方程就出来了（我不知道为什么要思考半天呢，还是傻了）\(f[i]=f[i-1]+2+f[i-f[i-1]-2]\) 但前提是括号要匹配上，还有一个重点是求出这个括号是什么，蒟蒻应该就不会了吧（虽然我是个会这个的蒟蒻），可以再设一个变量为能向左扩展到最远的边界，然后简单转移就好了。
感觉细节有点多，还是放一下吧
#include <bits/stdc++.h>
using namespace std;
const int N=1000005;
char s[N];
int r[N];
int x;
int f[N];
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>(s+1);
int n=strlen(s+1);
int ans=0;
for(int i=1;i<=n;i++){
if((s[i]==']'&&s[i-f[i-1]-1]=='[')||(s[i]==')'&&s[i-f[i-1]-1]=='(')){
f[i]=f[i-1]+2+f[i-f[i-1]-2];
r[i]=i-f[i-1]-1;
if(r[i-f[i-1]-2]!=0&&f[i-f[i-1]-2]!=0){
r[i]=r[i-f[i-1]-2];
}
if(f[i]>ans){
ans=max(ans,f[i]);
x=i;
}
}
else{
f[i]=0;
}
}
for(int i=r[x];i<=x;i++){
cout<<s[i];
}
return 0;
}
区间dp
P3146 [USACO16OPEN] 248 G
确实是比较模板的区间dp题，当两个子区间的值相同时且不为0时（没更新不能非法更新），则大区间为小区间值加一，在转移时取最大值即可。
P3147 [USACO16OPEN] 262144 P
一看题面，唉！和上面题是一样的，但是！一看数据范围，再见区间dp，我们要用一种全新的状态，设 \(f[i][k]\) 表 \(i\) 位置合并数值为 \(k\) 时，能向右扩展到最远的点，因为是最右，所以k最大。
那怎么转移呢，我们直觉经验告诉我们要从 \(k-1\) 转移过来，\(f[i][k]\) 为 0 表示没有找到最优解，此时我们就有 \(f[i][k]=f[f[i][k-1]][k-1]\) 这个式子很有深度，只有 \(f[i][k-1]\) 和 \(f[f[i][k-1]][k-1]\) 都有 \(k-1\) 的话就会进行转移，如何更新右端点，你可以在纸上画一画看看是不是这回事，转移后当然只有 \(f[i][k]\) 不为 0 才更新最大值。
这个我还是上个代码吧
#include <bits/stdc++.h>
using namespace std;
int n;
int f[262144][66];
int ans;
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
int x;
cin>>x;
f[i][x]=i+1;
ans=max(ans,x);
}
for(int k=1;k<=64;k++){
for(int i=1;i<=n;i++){
if(f[i][k]==0){
f[i][k]=f[f[i][k-1]][k-1];
}
if(f[i][k]){
ans=max(ans,k);
}
}
}
cout<<ans;
return 0;
}
P3205 [HNOI2010] 合唱队
巧妙的区间dp，使我脑子旋转，首先要想到是区间dp，因为这题是添加到最左最右，所以我们可以考虑一个数是左边区间和右边区间新添加的数，设状态为 \(f[i][j][0 ]\) 为区间 i-j 放数在最左边的方案数，则 \(f[i][j][1]\) 为区间 i-j 放数在最右边的方案数。
我们想右边已有一个区间，我们新插入的数放在了最左侧，我们要找到上一个插入的数，这个数要比他大才会让我到最左，此时只有区间的最左的数和最右的数可能会造成影响，于是我们就找到了转移。
如下图的形式：
然后我们设初始状态为 \(f[i][1][0]=1\) 默认每个数初始都是从左插入进来的（当然只设右也可以，但不要两个都初始化）
P9325 [CCC 2023 S2] Symmetric Mountains
终于有一眼秒的题了，确实非常简单，发现长度为1的区间可以推出区间3（只在区间1的左右加两个数，区间值只加了个差值）以此类推奇数区间都可以推出来了，那偶数区间也一样的推就可以了。
P2858 [USACO06FEB] Treats for the Cows G/S
又是一个逆天区间dp题，好不容易辉煌地秒了一道题，又给我打回原形了。
因为是向左和向右一个一个加值，所以和上面那个【合唱团】相似，然后我就想啊想，发现怎么玩啊！一看题解要反着想……
怎么反着想呢，每次加入一个递减的天数乘积，然后区间长度为 3 的最大值为区间为2 的最大值加上一个 3*val[i] （逆天数乘价格），看下图你一定会明白的（应该吧……？）
又是学到新东西的一天。
P1929 迷之阶梯
谜之解法，正常状态 \(f[i]\) 为 \(i\) 位置能到达最远的位置，有 \(f[i]=f[i-1] (a[i]==a[i-1])\) 并且转移进行跳跃操作，\(f[i]=min(f[i],f[j]+(j-k)+1)\)，这样 \(n^3\) 操作解决，这题主要学到的是向前转移。注意：位运算比加运算优先级低。
P1934 封印
你看刚学的新方法就用到了，和上面一样的处理方法，不断向前更新
正常状态 \(f[i]=a[i]\times n^2 +f[i-1]\)。
向前更新的转移 \(f[j]=min(f[j],f[k-1]+(a[j]+a[k])*(sum[j]-sum[k-1]))\)。
dp优化篇
数据结构优化
P1020 [NOIP1999 提高组] 导弹拦截
需要抽象一下，第一问就可以抽象为最长不上升子序列，第二问可以抽象为最长上升子序列长度。
就如下图的情况：
然后可以先 \(n^2\) 做法做，因为 \(n\ge 100000\) 所以要滚动数组，求最长不上升子序列可以反向从 n 开始递推。
我是 n^2 我不好
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+10;
int n;
int a[N];
int f[N];
int ans1,ans2;
int main(){
while(cin>>a[++n]);
n-=1;
for(int i=n;i>=1;i--){
f[i]=1;
for(int j=n;j>i;j--){
if(a[i]>=a[j]){
f[i]=max(f[i],f[j]+1);
}
}
ans1=max(ans1,f[i]);
}
for(int i=1;i<=n;i++){
f[i]=1;
for(int j=1;j<i;j++){
if(a[i]>a[j]){
f[i]=max(f[i],f[j]+1);
}
}
ans2=max(ans2,f[i]);
}
cout<<ans1<<"\n"<<ans2;
return 0;
}
但是这个复杂度是不可以接受的，我们考虑优化转移过程，转移状态数是少不了了，所以从转移成本优化，但 \(LIS\) 每次都要找到前面元素可转移的元素的最大值，可以用求最大值的数据结构优化，我们用树状数组优化。
我们维护 \(f[i]\) 为以 \(i\) 结尾的 \(LIS\) 长度的最大值，每次转移都查询 \(1,a[i]-1\) 中的最大值 \(（query(a[i]-1)）\)，找到最大值加一就是即为以 \(a[i]\) 结尾的最长长度，再把最大值加入到树状数组中\(（add(a[i],q+1)）\)
我是树状数组我厉害
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+10;
int n;
int mx=0;
int a[N];
int f[N];
int ans1,ans2;
int lb(int x){
return x&-x;
}
void add(int x,int y){
while(x<=mx){
f[x]=max(y,f[x]);
x+=lb(x);
}
}
int query(int x){
int ans=0;
while(x){
ans=max(ans,f[x]);
x-=lb(x);
}
return ans;
}
int main(){
while(cin>>a[++n]) mx=max(mx,a[n]);
n-=1;
for(int i=n;i>=1;i--){
int q=query(a[i]);
add(a[i],q+1);
ans1=max(ans1,q+1);
}
memset(f,0,sizeof f);
for(int i=1;i<=n;i++){
int q=query(a[i]-1);
add(a[i],q+1);
ans2=max(ans2,q+1);
}
cout<<ans1<<"\n"<<ans2;
return 0;
}
口胡一下不严谨的正确原因，树状数组查询的是 \(1-n\) 之间的最大值，新加入的数为 \(a\) 如果之前没有加入过比 \(a\) 还小的数就返回的是 \(0\) 也就是之前加入的所有的数比他小的最大值。
P1637 三元上升子序列
唉，我还是太菜了，这虽然就是一个最长上升子序列的题，但是这有固定的长度与要求求个数，又不太一样，所以讲下吧，希望你（我）能学会。
设状态为 f[i][j] 为以 a[j] 结尾的长度为 i 的上升子序列的个数。
然后我们就可以得到方程 \(f[i][j]=\sum_{a[k]<a[j],k<j}{f[i-1][k]}\)
设好状态方程这个式子还算很显然了，但是这个是暴力，复杂度是 \(O(n^2len)\)，有时是无法通过题的，所以我们要请出我们的优化了（还有高手！！）
这时就要请出我们的树状数组了，可以发现这个求和操作是影响复杂度的大头，而这个求和有一定的条件 \(a[k]<a[j],k<j\)
而树状数组也是将比他小的数全部加和，所以每次求和时直接 \(ask(a[j]-1)\)，然后再赋值 \(add(a[j],f[i-1][j])\)，然后还有一点就是树状数组搭配离散化更佳。
点击查看代码，这个可以看下
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e6+10;
#define int ll
int n;
int a[N],b[N];
int f[10][N];
int c[N];
int lb(int x){
return x&-x;
}
void add(int x,int k){
while(x<=n){
c[x]+=k;
x+=lb(x);
}
}
int query(int x){
int ans=0;
while(x){
ans+=c[x];
x-=lb(x);
}
return ans;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=a[i];
}
sort(b+1,b+n+1);
int m=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;i++){
a[i]=lower_bound(b+1,b+n+1,a[i])-b;
f[1][i]=1;
}
for(int len=2;len<=3;len++){
memset(c,0,sizeof c);
for(int i=1;i<=n;i++){
f[len][i]=query(a[i]-1);
add(a[i],f[len-1][i]);
}
}
int ans=0;
for(int i=1;i<=n;i++){
ans+=f[3][i];
}
cout<<ans;
return 0;
}
P11187 配对序列
每日唐诗操作大赏，非常离谱，赛时我都想到了向前推奇偶，但是我还是唐，应该用两维分开记录，而我用一个，唉，我也想到这点了，但不感觉不太可能，以后还是要大胆地写题啊！！！
最暴力方法，向前找到 \(j,k\) 其中要满足 \(a_i==a_j \&a_i!=a_k\) 然后就可以转移过来。
进步一点就是分奇序列和偶序列，相等可以从奇序列转移过来，不等可以从偶序列转移过来。
最进步的就是偶序列从上一个相等的数转移过来，奇序列从之前加入的数中最大的转移过来，这步可以用数据结构优化。
然后就是这样地做完了，真不知道为什么我这么唐，唉，真不知道之后会怎么样！！
前缀和优化
这可能是我第一个学会的dp优化！！。
51nod 2180 争渡
常记溪亭日暮，沉醉不知归路。兴尽晚回舟，误入藕花深处。争渡，争渡，惊起一滩鸥鹭。 ——李清照《如梦令·常记溪亭日暮》
给出线段上界和下界，要在严格递增地在区间内选数，问到最后一条线段的方案数。
见上图，第 \(i\) 条线段 \(j\) 点的方案数为 \(i-1\) 条线段的 \(j-1\) 到 \(l[i-1]\) 的方案数的总和。
所以我们可以得到设状态为 dp[i][j] 前 i 条线段点数为 j 的方案数，我们也可以得到动态转移方程 \(dp[i][j]=\sum_{k=l[i-1]}^{j-1} dp[i-1][k]\)
但是这样做的时间复杂度有点高，那如何优化呢。
考虑使用前缀和优化，我们用 sum 数组将上方的求和储存起来，这样就不用每次都需要重复计算一次了。
总复杂度为 \(O(n\times M)\)，\(M\) 为值域。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
const int mod=998244353;
int n;
int l[N],r[N];
int dp[205][N];
int sum[N];
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
cin>>l[i]>>r[i];
}
for(int i=l[1];i<=r[1];i++){//初始化方案数
dp[1][i]=1;
}
for(int i=0;i<=N;i++){//求前缀和
sum[i]=(sum[i-1]+dp[1][i])%mod;
}
for(int i=2;i<=n;i++){//从第二个开始
for(int j=l[i];j<=r[i];j++){//O(1) 获取方案数
dp[i][j]=sum[j-1];
}
sum[0]=0;//初始化，重置数组
for(int j=0;j<=N;j++){//再次求前缀和
sum[j]=(sum[j-1]+dp[i][j])%mod;
}
}
long long ans=0;
for(int i=l[n];i<=r[n];i++){//统计方案数
ans=(ans+dp[n][i])%mod;
}
cout<<ans;
return 0;
}
树形dp
树上背包
P2014 [CTSC1997] 选课
树上背包的模板题，我简单口胡，剩下的%%%大佬
因为有没父节点的点，将他们与0节点相连，总m也要增加，因为根0是必选的，所以设状态为 \(dp[i][j]\) 为节点 i 体积为 j 时的最大价值，因为节点的重量不确定，所以不仅要枚举总重量，还要枚举子节点的重量。
其实好像和分组背包相似的。
点击查看代码，看看学习学习
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=500+10;
int n,m;
int f[N][N];
vector<int> v[N];
void dfs(int x){
for(int i=0;i<v[x].size();i++){
dfs(v[x][i]);
}
for(int i=0;i<v[x].size();i++){
for(int j=m;j>=1;j--){
for(int k=0;k<j;k++){
int y=v[x][i];
f[x][j]=max(f[x][j],f[x][j-k]+f[y][k]);
}
}
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m;
m++;
for(int i=1;i<=n;i++){
int u;
cin>>u>>f[i][1];
v[u].push_back(i);
}
dfs(0);
cout<<f[0][m];
return 0;
}
P1273 有线电视网
虽然也是树上背包的模板题，但是 这个大佬 说了个很重要的观点，树上背包就是分组背包。
组数就是子树个数，组内元素就是该子树选前i个节点的最大价值和，重量就是子树大小。
好了，你可以去看大佬博客了，我总结的非常不到位，但是你可以看看代码。
没事第一次学肯定不会，所以才就多练！！！！
点击查看代码，菜就多练
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=3010;
int n,m;
int val[N];
int f[N][N];
struct ss{
int vv,w;
};
vector<ss> v[N];
int dfs(int x){
if(x>n-m){
f[x][1]=val[x];
return 1;
}
int sum=0;
for(int i=0;i<v[x].size();i++){
int y=v[x][i].vv;
int t=dfs(y);
sum+=t;
for(int j=sum;j>0;j--){
for(int k=1;k<=t;k++){
if(j-k>=0){
f[x][j]=max(f[x][j],f[x][j-k]+f[y][k]-v[x][i].w);
}
}
}
}
return sum;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
memset(f,-0x3f,sizeof f);
cin>>n>>m;
for(int i=1;i<=n-m;i++){
int u,vv,w;
cin>>u;
for(int j=1;j<=u;j++){
cin>>vv>>w;
v[i].push_back({vv,w});
}
}
for(int i=n-m+1;i<=n;i++){
cin>>val[i];
}
for(int i=1;i<=n;i++){
f[i][0]=0;
}
int x=dfs(1);
for(int i=m;i>=1;i--){
if(f[1][i]>=0){
cout<<i;
break;
}
}
return 0;
}
P1040 [NOIP2003 提高组] 加分二叉树
我非常菜只看到了 dp，然后不会了，但是这题只有 \(3\) 种类型，根节点、左节点、右节点，所以我们处理区间的时候枚举根就好了，因为是中序遍历，左边的是左子树，右边的是右子树，直接转移即可 \(f[l][r]=max(1,f[l][k-1])*max(1,f[k+1][r])+f[k][k]\)，记录前序遍历只需记录区间最大值时的根节点然后递归遍历。
P2585 [ZJOI2006] 三色二叉树
很暴力的一种树上dp，设状态 \(f[i][0/1/2]\) 表示 \(i\) 好节点分别涂 绿/蓝/红 的绿节点的最大值，当然最小值也一样维护，转移时直接暴力转移即可，最后取根节点分别涂 \(3\) 种颜色的最大值。
P3047 [USACO12FEB] Nearby Cows G
很绕的一道题，而且题面改了和题解对不上了，就有点难受了，而且要用容斥或换根，学数学的有福了。
首先设状态为 \(f[i][j]\) 表示i节点j步以内节点权值和，那就可以递推到根节点了。
第二遍dfs就要求子节点的权值了，但如果直接转移 \(f[y][j]=\sum{f[x][j-1]}\) 不是很对如下大佬的图。
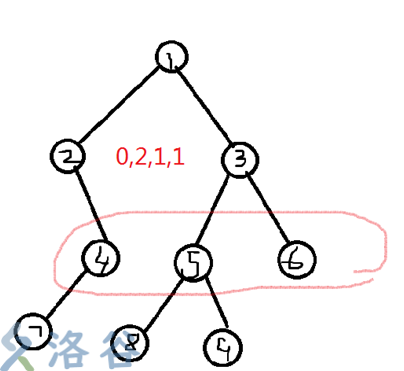
会有重复的点计算，所以还要在容斥减去 \(f[x][j-2]\)。
确实复杂上个代码，点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
const int M=1e6+10;
#define ull unsigned long long
#define ll long long
#define pi pair<int,int>
#define ls p<<1;
#define rs p<<1|1
#define int ll
int n,m,k;
vector<int> v[N];
int f[N][25];
int a[N][25];
void dfs1(int x,int fa){
for(int i=1;i<=k;i++){
f[x][i]=f[x][i-1];
}
for(int i=0;i<v[x].size();i++){
int y=v[x][i];
if(y!=fa){
dfs1(y,x);
for(int j=1;j<=k;j++){
f[x][j]+=f[y][j-1];
}
}
}
}
void dfs2(int x,int fa){
for(int i=0;i<v[x].size();i++){
int y=v[x][i];
if(y!=fa){
a[y][1]+=f[x][0];
for(int j=2;j<=k;j++){
a[y][j]+=a[x][j-1]-f[y][j-2];
}
dfs2(y,x);
}
}
}
signed main(){
ios::sync_with_stdio(false);
cin>>n>>k;
for(int i=1;i<=n-1;i++){
int u,vv;
cin>>u>>vv;
v[u].push_back(vv);
v[vv].push_back(u);
}
for(int i=1;i<=n;i++){
cin>>f[i][0];
}
dfs1(1,0);
for(int i=1;i<=n;i++){
for(int j=0;j<=k;j++){
a[i][j]=f[i][j];
}
}
dfs2(1,0);
for(int i=1;i<=n;i++){
cout<<a[i][k]<<"\n";
}
return 0;
}
状压dp
这个dp的复杂度通常是不下于 \(O(2^n)\)，所以有些时候看到n很小的时候可以考虑用他。
P3052 [USACO12MAR] Cows in a Skyscraper G
对选择物品的状态枚举，设状态 \(f[i]\) 为状态为 \(i\) 时所需组的最少数，再设一个数组表示该状态剩余的空间，于是有以下代码。
状压的特点是对未来状态影响。
不想写latex了，反正给自己看的
for(int i=0;i<=(1<<n)-1;i++){//状态
for(int j=1;j<=n;j++){//枚举物品
if(i&(1<<(j-1))){//已有跳过
continue;
}
if(g[i]>=a[j]&&f[i|(1<<(j-1))]>=f[i]){//能放下且放下后的状态所需组数是不少于我们的，这样才可以转移
f[i|(1<<(j-1))]=f[i];
g[i|(1<<(j-1))]=max(g[i|(1<<(j-1))],g[i]-a[j]);
}
else if(g[i]<a[j]&&f[i|(1<<(j-1))]>=f[i]+1){
f[i|(1<<(j-1))]=f[i]+1;
g[i|(1<<(j-1))]=max(g[i|(1<<(j-1))],w-a[j]);
}
}
}
P2622 关灯问题II
正常思维肯定就枚举开关状态了，但这题数据不允许（按钮多不能枚举按钮做状态），因为要求最少按钮数，所以bfs状态，然后枚举按钮，当全部灯都灭了就是当前按钮数，这是一个最短路的过程。
P8687 [蓝桥杯 2019 省 A] 糖果
注意这题的选择少可以枚举选择作状态，上面那题是最终状态少选择多。
既然选择少我们就枚举选择做状态，然后再枚举每袋糖果向后更新，但是我们不要在枚举状态时反复更新，我们选这袋糖果的最终状态只会有一种，我们可以提前预处理出来选这袋糖果最终状态，枚举当前状态时按位与即可。
点击查看代码
for(int i=0;i<(1<<m)-1;i++){
for(int j=1;j<=n;j++){
int y=i|vis[j];
if(f[y]>=f[i]+1){
f[y]=f[i]+1;
}
}
}
P4802 [CCO2015] 路短最
因为不能经过重复的点，所以考虑状压dp，压缩经过哪些点，设 \(f_{i,j}\) 表示选点情况为 \(i\) 时，我在 \(j\) 点的最长路距离，此时边是选择，我们枚举边，于是有 \(f_{i,v}=\max{f_{i,v},f_{i-(1<<(v-1)),u}+a_{u,v}}\)，然后最后我们枚举选起点终点中间全部的选点状态即可 \(ans=\max{ans,f_{i,n}}\)。
枚举边的话要枚举起点终点判断是否有连边，而起点与终点一定是状态上有的点，所以可以用 lowbit 优化一点，但也无所谓了。
P2704 [NOI2001] 炮兵阵地
说句闲话
很好的状压dp题，学完了这个你就知道了状压dp的套路题了，和区间dp一样看到后能很快地推出来，还有一题和这题一样的是P1896 [SCOI2005] 互不侵犯，但是这题比这题简单所以我就不说了（鸽：咕咕）。
初步分析
看到范围就放心大胆地去状压，我们设状态为 \(f_{s,t,i}\) 表示到第i行，这一行的状态为 \(t\)，上一行的状态为 \(s\)，总的放下的炮兵数。
我肯定要把上一行的答案转移过来吧，所以有转移方程 \(f_{s,t,i}=\max{f_{s,t,i},f_{ls,s,i-1}+sum_i}\)，\(ls\) 表示上上行，\(sum\) 是本行状态放下的炮兵数，所以我们就要枚举本行、上一行、上上一行的状态。
判断合法
这也是很重要的一点，我们分别看哪些条件不可以放炮兵。
- 不得放山地上：
这个可以在读入时把本行的平原山地用二进制表示出来（山地：1，平原：0）在判断是否可以选这个状态时按位与一下，如果不为 \(0\) 表明有炮兵在山地上，不合法。
- 上行或上上行有炮兵会攻击到：
因为我们枚举了上行与上上行的状态，所以我们直接按位与，不等于0说明会攻击到，不和法。
- 左右2行炮兵会攻击到：
如果我们将本行状态二进制向左移一，再按位与发现不等于0，就说明我向左攻击一格就会达到一个炮兵，不合法，当然还有左移2。
最后统计最后一行所有合法状态的放炮兵的最大值就好了。
空间开这么大会爆的，所以滚动下数组就好了。
数位dp
P2602 [ZJOI2010] 数字计数
比较有趣的数位dp模板题，虽然我想不出来，但是我现在最好是不要忘了就行吧。
设 \(f[i]\) 表示 \(i\) 位数每个数字出现的次数，于是我们有这个式子 \(f[i]=f[i-1]\times 10^i/10\)，可以想一想，然后我们处理每一位数字，把低位的都统计上，再统计这位数字的出现次数，再减去这位为0的情况，要认真学习看其他大佬的讲解吧。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=15;
#define ll long long
#define int ll
int f[N];
int a[N];
int n;
int cnta[N];
int cntb[N];
int sum[N];
void init(){
a[0]=1;
for(int i=1;i<=15;i++){
f[i]=i*a[i-1];
a[i]=a[i-1]*10;
}
}
void solve(int x,int *cnt){
int len=0;
while(x){
sum[++len]=x%10;
x/=10;
}
for(int i=len;i>=1;i--){
for(int j=0;j<=9;j++){
cnt[j]+=f[i-1]*sum[i];
}
for(int j=0;j<sum[i];j++){
cnt[j]+=a[i-1];
}
ll sum2=0;
for(int j=i-1;j>=1;j--){
sum2=sum2*10+sum[j];
}
cnt[sum[i]]+=sum2+1;
cnt[0]-=a[i-1];
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
init();
int l,r;
cin>>l>>r;
solve(l-1,cnta);
solve(r,cntb);
for(int i=0;i<=9;i++){
cout<<cntb[i]-cnta[i]<<" ";
}
return 0;
}
