51nod 1274 最长递增路径

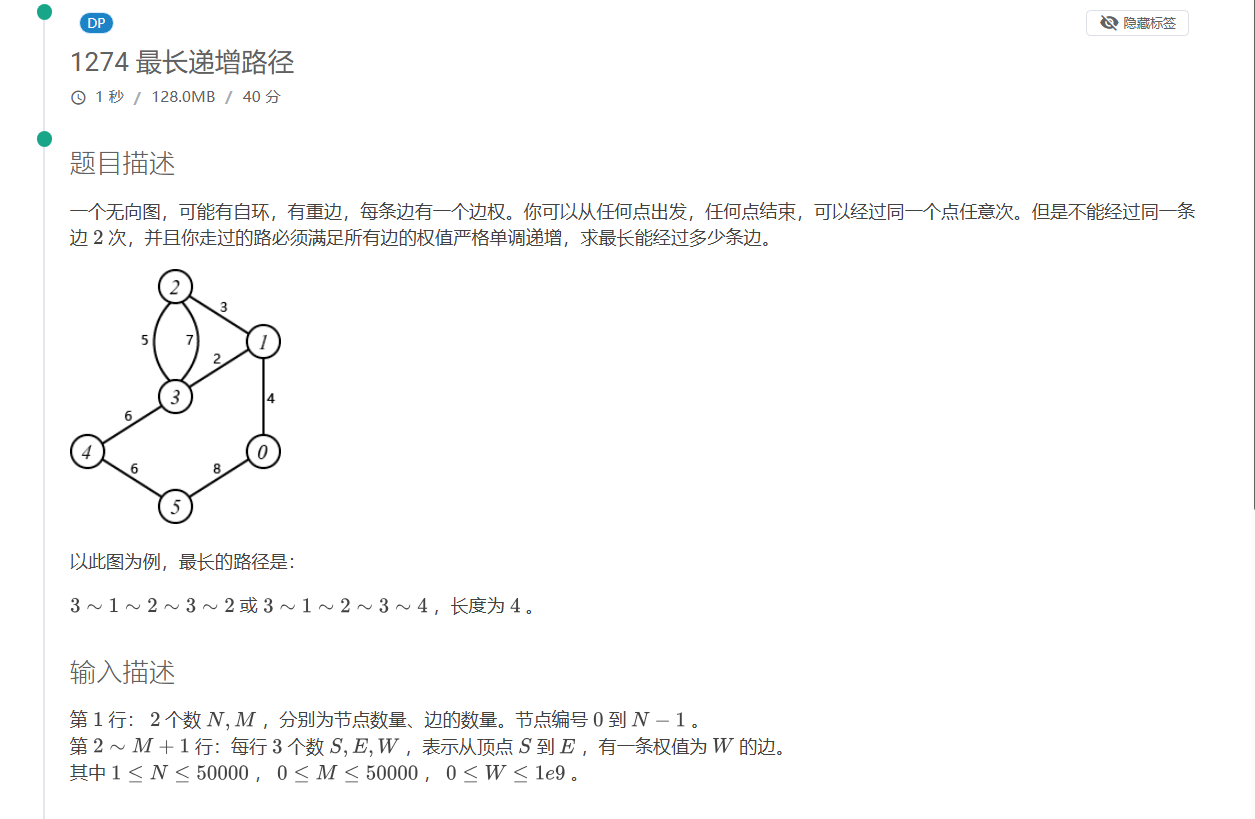
因为边权递增，按最小生成树的顺序 dp，设状态 \(dp[i]\) 为 \(i\) 点的最长路径长度，但是需要单调递增，所以考虑可以同时更新（先将原dp数组储存下来，再用新数组的值更新原 dp 数组），答案为 \(max(dp[i])\)。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=5e5+10;
int n,m;
struct ss{
	int u,v,w;
}e[N];
bool cmp(ss g,ss h){
	return g.w<h.w;
}
ll dp[N],f[N];
int main() { 
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1;i<=m;i++){
    	cin>>e[i].u>>e[i].v>>e[i].w; 
	}
	sort(e+1,e+1+m,cmp);
	int last=0;
	for(int i=1;i<=m;i++){
		if(e[i].w==e[i+1].w){
			continue; 
		}
		for(int j=last+1;j<=i;j++){
			f[e[j].u]=dp[e[j].u];
			f[e[j].v]=dp[e[j].v];
		}
		for(int j=last+1;j<=i;j++){
			dp[e[j].u]=max(dp[e[j].u],f[e[j].v]+1);
			dp[e[j].v]=max(dp[e[j].v],f[e[j].u]+1);
		}
		last=i;
	}
	ll ans=0;
	for(int i=0;i<n;i++){
		ans=max(ans,dp[i]);
	}
	cout<<ans;
    return 0;
}