【算法学习】tarjan 强连通、点双、边双及其缩点 重磅来袭！！！！

原来那篇笔记完全不行了，我将原先的笔记全部重写，写一个真正好用的模板库。

强连通分量

通俗易懂的讲就是有向图，简称 SCC。

缩点

强连通分量上的环有特殊的性质，因为他们可以相互到达，所以我们可以将环化为点，然后这就变为了一个 有向无环图DAG 然后我们就可以进行 dp、最短路等多种操作。

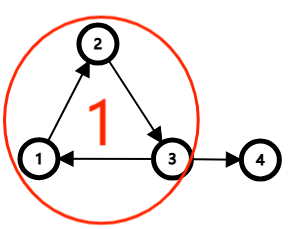
image

tarjan 缩点

新人肯定听的懵懵，但尽量听。

首先我们定义：

  • \(dfn\) 为该点访问次序，就是 dfs 序。

  • \(low\) 就是这个点能到达dfs序最小的点的dfs序是多少。

  • \(vis\) 表示这个点是否在栈中。

  • \(of\) 这个点所属缩点的编号。

我们从根节点开始依次访问每个点，然后把这个点放入栈中，枚举出点，如果下一个点没访问过就访问更新 \(low\)，如果访问过就判断是否在栈中然后更新 \(low\)，访问完所以点之后如果这个点的 dfn 和 \(low\) 相同则我们从栈顶到当前点 \(x\) 的所有点都在同一个环内。

为什么这么做对的呢，我们简单速通一下，如果他能到达访问编号比他小的点那他就不会退栈，直到回溯到不能访问到比他还小的点，那他就作为根？把栈中这一部分都收下来，如果图是一条链的话就只会收下自己。

具体退栈回溯里面的内容可以自由添加，比如权值大小什么的。

还是那句：不懂可以 GDB 调试跟着顺一遍。

#include <bits/stdc++.h>
#define int long long
const int N=5e5+10;
using namespace std;
 
int n,m;
 
int head[N];
int cnt=1;
struct ss{
	int to,next; 
}e[N];
 
void add(int u,int v){
	e[++cnt].to=v;
	e[cnt].next=head[u];
	head[u]=cnt;
}
 
int dfn[N],low[N],st[N],vis[N],top,t,tot,of[N];
 
 
void tarjan(int x){
	dfn[x]=low[x]=++t;
	st[++top]=x;
	vis[x]=1;
 
	for(int i=head[x];i;i=e[i].next){
		int y=e[i].to;
		if(!dfn[y]){
			tarjan(y);
			low[x]=min(low[x],low[y]);
		}
		else if(vis[y]==1){
			low[x]=min(low[x],dfn[y]);	
		}
	}
	if(dfn[x]==low[x]){
		int b=-1;
		tot++;
		while(x!=b){
			b=st[top--];
			of[b]=tot;
			vis[b]=0;
		}
	}
}
 
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 
	cin>>n>>m;
 
	for(int i=1;i<=m;i++){
		int u,vv;
		cin>>u>>vv;
		add(u,vv);
		add(vv,u);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			tarjan(i);
		}
	}
	return 0;
}

为何要判断是否在栈中才更新是因为他们不一定在同一次 tarjan 中更新，多次 tarjan 的原因也是应对下面这张图。

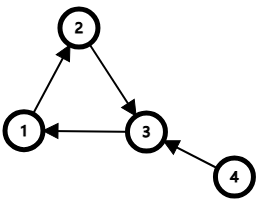
image

双连通分量

非常通俗来说就是无向图。

割点

删掉这个点之后整个图不连通了，那这个点就是割点。

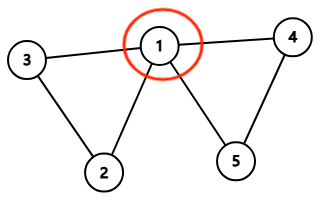
image

tarjan 求割点

如果一个点 \(x\) 的子孙不通过 \(x\) 而可以通过一条返祖边到达 \(x\) 及其祖先即 \(dfn[x]>low[x]\)，那他就不是割点，相反如果子孙无法到达即 \(dfn[x]<=low[x]\)，那他就是割点。

注意：根节点是个例外，因为他没有祖先所以要特判如果他有两个及以上的属于不同连通分量的子孙，那他就是割点（具体见上图）。

#include <bits/stdc++.h>
#define int long long
const int N=5e5+10;
using namespace std;
 
int n,m;
 
int head[N];
int cnt=1;
struct ss{
	int to,next;
}e[N];
void add(int u,int v){
	e[++cnt].to=v;
	e[cnt].next=head[u];
	head[u]=cnt;
}
 
int dfn[N],low[N],st[N],t,is[N];
int root;
 
void tarjan(int x){
	dfn[x]=low[x]=++t;
	
	int son=0;
	for(int i=head[x];i;i=e[i].next){
		int y=e[i].to;
		if(!dfn[y]){
			son++;
			tarjan(y);
			low[x]=min(low[x],low[y]);
 
			if(dfn[x]<=low[y]&&x!=root){
				is[x]=1;
			}
		}
		else{
			low[x]=min(low[x],dfn[y]);
		}
	}
	if(x==root&&son>=2){
		is[x]=1;
	}
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
	cin>>n>>m;
 
	for(int i=1;i<=m;i++){
		int u,vv;
		cin>>u>>vv;
		add(u,vv);
		add(vv,u);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			root=i;
			tarjan(i);
		}
	}
	return 0;
}

点双连通分量 e-dcc

简单来说就是没有割点的连通分量（无向图）。

tarjan 求点双连通分量及其缩点

用栈来储存点，然后找到割点时弹栈即可。

因为点双的性质中，两个点双最多只有一个公共点且这个公共点为割点，我们找到所有的点双之后用割点将两个点双连接起来。

单点也是割点，也属于一个点双。

#include <bits/stdc++.h>
#define int long long
const int N=7e5+10;
const int M=4e6+10;
using namespace std;
 
int n,m;
 
int head[N];
int cnt=1;
struct ss{
	int to,next;
}e[M];
void add(int u,int v){
	e[++cnt].to=v;
	e[cnt].next=head[u];
	head[u]=cnt;
}
 
int dfn[N],low[N],st[N],top,t,is[N],tot;
vector<int> dcc[N];
int root;
 
void tarjan(int x){
	dfn[x]=low[x]=++t;
	st[++top]=x;
	
	if(root==x&&!head[x]){//单点也是割点
		dcc[++tot].push_back(x);
		return;
	} 
	
	int son=0;
	for(int i=head[x];i;i=e[i].next){
		int y=e[i].to;
		if(!dfn[y]){
			son++;
			tarjan(y);
			low[x]=min(low[x],low[y]);
 
			if(dfn[x]<=low[y]){
				if(x!=root||son>1){
					is[x]=1;
				} 
				tot++;
				int b=-1;
				do{
					b=st[top--];
					dcc[tot].push_back(b);
				}while(y!=b);
				dcc[tot].push_back(x);//割点不弹出
			}
		}
		else{
			low[x]=min(low[x],dfn[y]);
		}
	}
}
 
int of[N]; 
 
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
	cin>>n>>m;
 	
	for(int i=1;i<=m;i++){
		int u,vv;
		cin>>u>>vv;
		if(u!=vv){
			add(u,vv);
			add(vv,u);	
		}
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			root=i;
			tarjan(i);
		}
	}
	
	cout<<tot<<"\n";
	
	for(int i=1;i<=tot;i++){
		cout<<dcc[i].size()<<" ";
		for(int j=0;j<dcc[i].size();j++){
			cout<<dcc[i][j]<<" ";
		}
		cout<<"\n";
	}
	
	//缩点
	
	int cnt2=tot;//重新赋编号
	for(int i=1;i<=n;i++){
		if(is[i]){
			of[i]=++cnt2;
		}
	}
	memset(head,0,sizeof head);
	memset(e,0,sizeof e);
	cnt=1;
	//割点连边
	for(int i=1;i<=tot;i++){
		for(int j=0;j<dcc[i].size();j++){
			int x=dcc[i][j];
			if(is[x]){
				add(i,of[x]);
				add(of[x],i);
			}
			else{
				of[x]=i;
			}
		}
	}
	
	for(int i=1;i<=n;i++){
		cout<<of[i]<<" ";
	}
	return 0;
}

割边（桥）

在无向图中，删掉这条后图不连通，那这条边就是割边。

tarjan 求割边

和割点的思路一样，不过没有根节点之类的限制了，如果一个点 \(x\) 的子孙不通过 \(x\) 的出边而可以通过一条返祖边到达 \(x\) 及其祖先即 \(dfn[x]\ge low[x]\)，那这条边就不是割边，反之就是割边。

注意：割点是允许回路而割边不允许。

#include <bits/stdc++.h>
#define int long long
const int N=5e5+10;
using namespace std;
 
int n,m;
 
int head[N];
int cnt=1;
struct ss{
	int u,v,next;
}e[N];
void add(int u,int v){
	e[++cnt].v=v;
	e[cnt].u=u;
	e[cnt].next=head[u];
	head[u]=cnt;
}
 
int dfn[N],low[N],st[N],t,is[N];
 
void tarjan(int x,int edge){
	dfn[x]=low[x]=++t;
	
	for(int i=head[x];i;i=e[i].next){
		int y=e[i].v;
		if(!dfn[y]){
			tarjan(y,i);
			low[x]=min(low[x],low[y]);
 
			if(dfn[x]<low[y]){
				is[i]=is[i^1]=1;
			}
		}
		else if(i!=(edge^1)){
			low[x]=min(low[x],dfn[y]);
		}
	}
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
	cin>>n>>m;
 
	for(int i=1;i<=m;i++){
		int u,vv;
		cin>>u>>vv;
		add(u,vv);
		add(vv,u);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			tarjan(i,0);
		}
	}
	
	for(int i=2;i<=cnt;i+=2){
		if(is[i]){
			cout<<e[i].u<<" "<<e[i].v<<"\n";
		}
	}
	return 0;
}

边双连通分量 e-dcc

无向图内没有割边。

tarjan 求边双连通分量及缩点

也是求出割边之后求边双连通分量的话可以将割边全部都删去然后就只剩下边双了，缩点的话像强连通分量一样缩点就可以了。

#include <bits/stdc++.h>
#define int long long
const int N=4e6+1e5;
using namespace std;
 
int n,m;
 
int head[N];
int cnt=1;
int uu[N],vv[N];
struct ss{
	int u,v,next;
}e[N];
void add(int u,int v){
	e[++cnt].v=v;
	e[cnt].u=u;
	e[cnt].next=head[u];
	head[u]=cnt;
}
 
int dfn[N],low[N],st[N],t,is[N],tot;
 
void tarjan(int x,int edge){
	dfn[x]=low[x]=++t;
	
	for(int i=head[x];i;i=e[i].next){
		int y=e[i].v;
		if(!dfn[y]){
			tarjan(y,i);
			low[x]=min(low[x],low[y]);
 
			if(dfn[x]<low[y]){
				is[i]=is[i^1]=1;
			}
		}
		else if(i!=(edge^1)){
			low[x]=min(low[x],dfn[y]);
		}
	}
}
 
int of[N];
vector<int> dcc[N];
 
void dfs(int x){
	of[x]=tot;
	dcc[tot].push_back(x);
	for(int i=head[x];i;i=e[i].next){
		int y=e[i].v;
		if(!is[i]&&!of[y]){
			dfs(y);
		}
	}
}
 
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
	cin>>n>>m;
 
	for(int i=1;i<=m;i++){
		cin>>uu[i]>>vv[i];
		if(u[i]!=vv[i]){
			add(uu[i],vv[i]);
			add(vv[i],uu[i]);	
		} 
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			tarjan(i,0);
		}
	}
	
	for(int i=1;i<=n;i++){
		if(!of[i]){
			tot++;
			dfs(i);
		}
	}
	
	cout<<tot<<"\n";
	
	for(int i=1;i<=tot;i++){
		cout<<dcc[i].size()<<" ";
		for(int j=0;j<dcc[i].size();j++){
			cout<<dcc[i][j]<<" ";
		}
		cout<<"\n";
	}
	
	//缩点
	memset(head,0,sizeof head);
	memset(e,0,sizeof e);
	cnt=1;
	
	for(int i=1;i<=m;i++){
		int x=uu[i],y=vv[i];
		if(of[x]!=of[y]){
			add(of[x],of[y]);
			add(of[y],of[x]);
		}
	}
	return 0;
}
posted @   sad_lin  阅读(40)  评论(0)  编辑  收藏  举报
相关博文：
·  LCA 最近公共祖先（树链和倍增）这次真有树链了！！！
·  动态规划专项训练 1
·  【7】Tarjan学习笔记
·  Tarjan 求强连通分量和缩点
·  Tarjan学习笔寄
阅读排行：
· winform 绘制太阳，地球，月球 运作规律
· TypeScript + Deepseek 打造卜卦网站：技术与玄学的结合
· Manus的开源复刻OpenManus初探
· 写一个简单的SQL生成工具
· AI 智能体引爆开源社区「GitHub 热点速览」
点击右上角即可分享
微信分享提示