基于Mathematica的图形刚体变换的几种实现方法

Mathematica操作

首先，优先使用系统内置函数实现，与此相关的内置函数包括Translate/TranslationTransform、Rotate/RotationTransform这几个常用的。每个函数在不同的场景下有不同的优势。

• 实例1:使用系统内置“动词”函数

(*使用系统内置“动词”函数*)
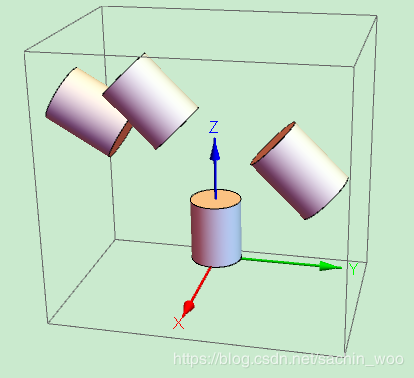
cube = Cylinder[{{0, 0, 0}, {0, 0, 0.5}}, 0.2];   (*生成一个圆柱体*)
cube1 = Rotate[Translate[cube, {1, 1, 1}],  45 Degree, {1, 0, 0}];   
 (*使用系统自带动作变换函数进行变换，先平移，再旋转*)

• 实例2:使用系统内置“名词”函数

(*使用系统内置“名词”函数*)
cube = Cylinder[{{0, 0, 0}, {0, 0, 0.5}}, 0.2];   (*生成一个圆柱体*)
cube2 = GeometricTransformation[GeometricTransformation[cube, TranslationTransform[{1, 1,1}]], 
   RotationTransform[60 Degree, {1, 0, 0}]];(*使用系统自带名词变换函数进行变换，先平移，再旋转*)

• 实例3:使用自定义函数

 (*使用自定义函数*)
SetDirectory["Z:\Wushuichuan\05-计算仿真\基于Mathematica机器人仿真\Packages"];
<< Screws.m
transform[shape_, g_] := GeometricTransformation[shape, TransformationFunction[g]]  (*定义图形变换函数*)
r = {{1, 0, 0}, {0, Cos[45 Degree], -Sin[45 Degree]}, {0,  Sin[45 Degree], Cos[45 Degree]}};  (*定义一个绕X轴旋转45度对应的矩阵*)
p = {1, 1,  1};      (*生成一个平移向量*)
g = RPToHomogeneous[r, p];     (*生成一个4x4的变换矩阵*)
cube = Cylinder[{{0, 0, 0}, {0, 0, 0.5}}, 0.2];   (*生成一个圆柱体*)
cube3 = transform[cube, g];     (*使用自定义图形变函数进行变换*)

后记

1. 以上每种方法在不同的场景均有不同的优势，要灵活运用，主要是函数参数的形式不一样。具体应用可以参考Wolfram参考资料。
2. 注意系统内置动词性函数和名词性函数的区别，一般情况下，动词性 函数可单独使用，名词性函数要配合其它函数使用，如实例2中要配合GeometricTransformation函数使用。名词性函数只是产生了一个相应的变换矩阵，且告诉系统这不是一个一般的矩阵，这是一个变换用的矩阵。
3. 实例3中的自定义函数和实例2中的名词性函数有相似之处，这个相似性与TransformationFunction有关，名词性变换函数产生的是一个变换矩阵，一般的变换矩阵不能直接用于变换，必须要由TransformationFunction函数来告知系统这是一个变换矩阵，经它处理后就可以当作GeometricTransformation的参数作为变换矩阵用于变换了。