导数微分积分的粗浅理解
我对这几个概念粗浅的理解:
导数:
对于一个方程:y=f(x),在某点的导数就是该点的切线的斜率,也即:f'(x) = dy/dx 。对于P0点的导数,就是角度∂的tan值,但是一般也不容易计算,所以可以用lim求极限的方式,也即计算PP0线无限接近P0的tan角度的值。
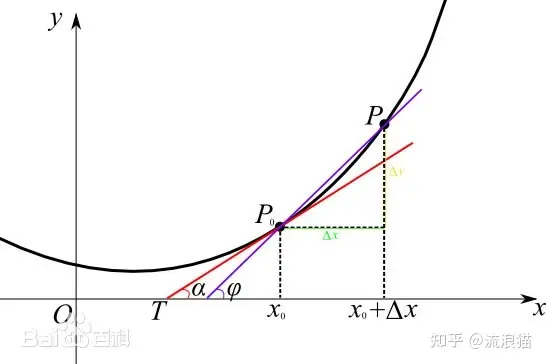
微分的定义可以粗略的人为是:dy = f'(x)dx
积分就是要把微小的汇集起来。我的理解是不定积分和定积分的定义是分开的,然后由定理推断出两者的关联关系。
不定积分:
其实是根据已知的微分来求原函数。如下的公式中G(x)的导数是g(x),而g(x)dx是微分的定义,所以定义不定积分就是已知一个函数的微分来求原函数。
![]()
定积分的概念:
尽管不定积分和定积分在公式的书写上很相近,但两者的定义却是隔离的,几乎看不出联系。定积分的定义是说对一个函数f(x),求解其在区间内的面积之和。例如:
![]()
因此我们刚开始的时候不要纠结两者之间的联系,单独看就可以了,后面伟人会证明两者之间简洁的关系。
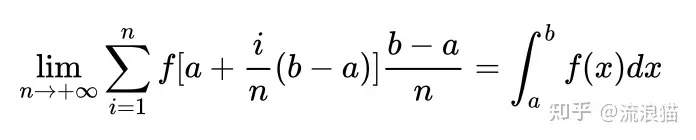
其几何含义就是函数f(x)在区间a,b之间的面积。
牛顿莱布尼茨公式
这个公式把定积分和不定积分的关系关联了起来。
![]() ,也即原函数在a,b两点的差值,也即不定积分在a,b两点间的差值。这就是两者之间的关系。
,也即原函数在a,b两点的差值,也即不定积分在a,b两点间的差值。这就是两者之间的关系。
以前我曾错误的认为是f(x)在区间的差值,这样的错误想法在几何上怎么也想不明白,但其实是f(x)的原函数F(x)在区间的值的差,这样在几何上就可以解释了。也参见这个视频的讲解:【牛顿-莱布尼茨公式】的动画证明_哔哩哔哩_bilibili ,其中的几张截图如下:
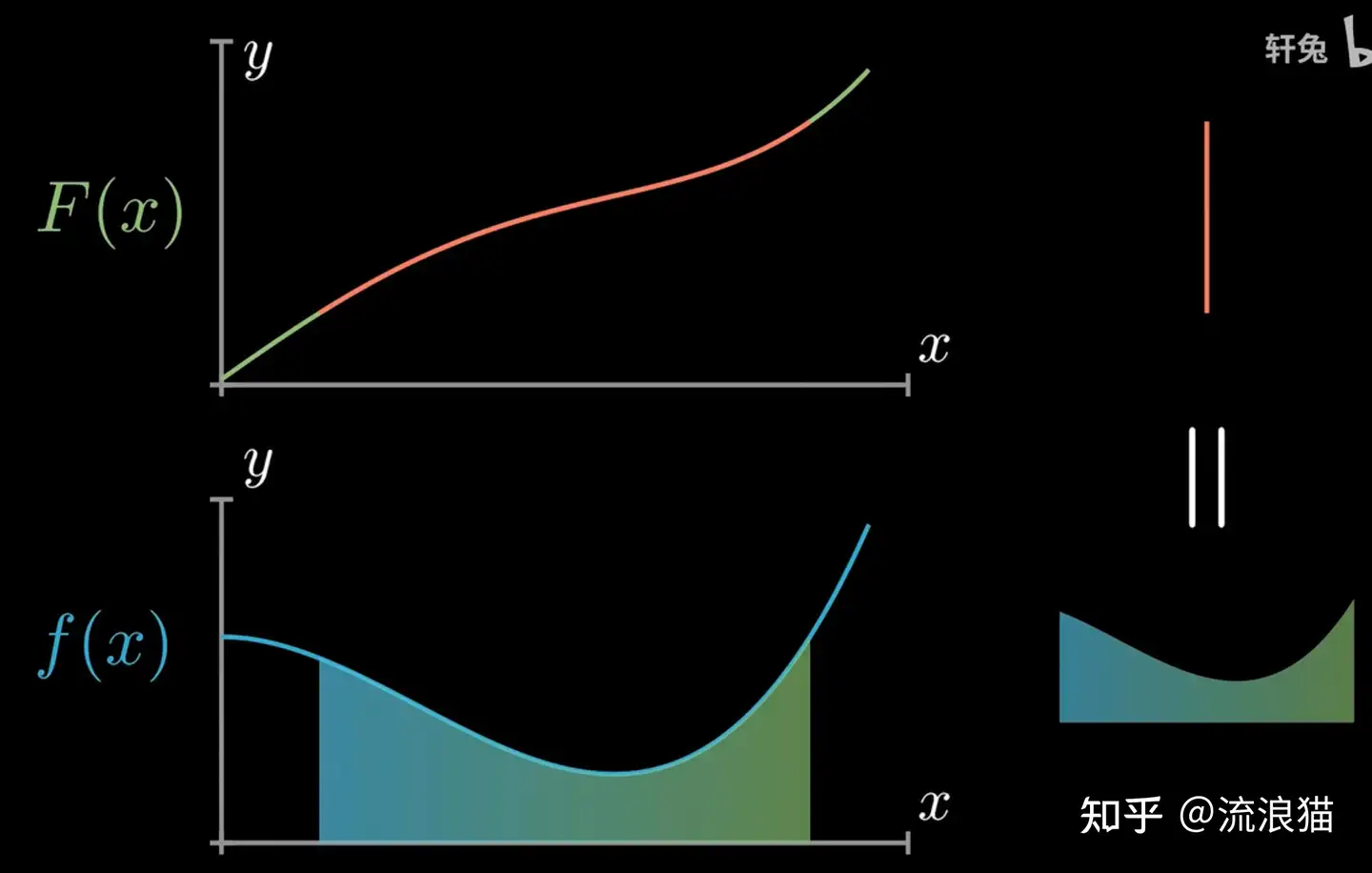
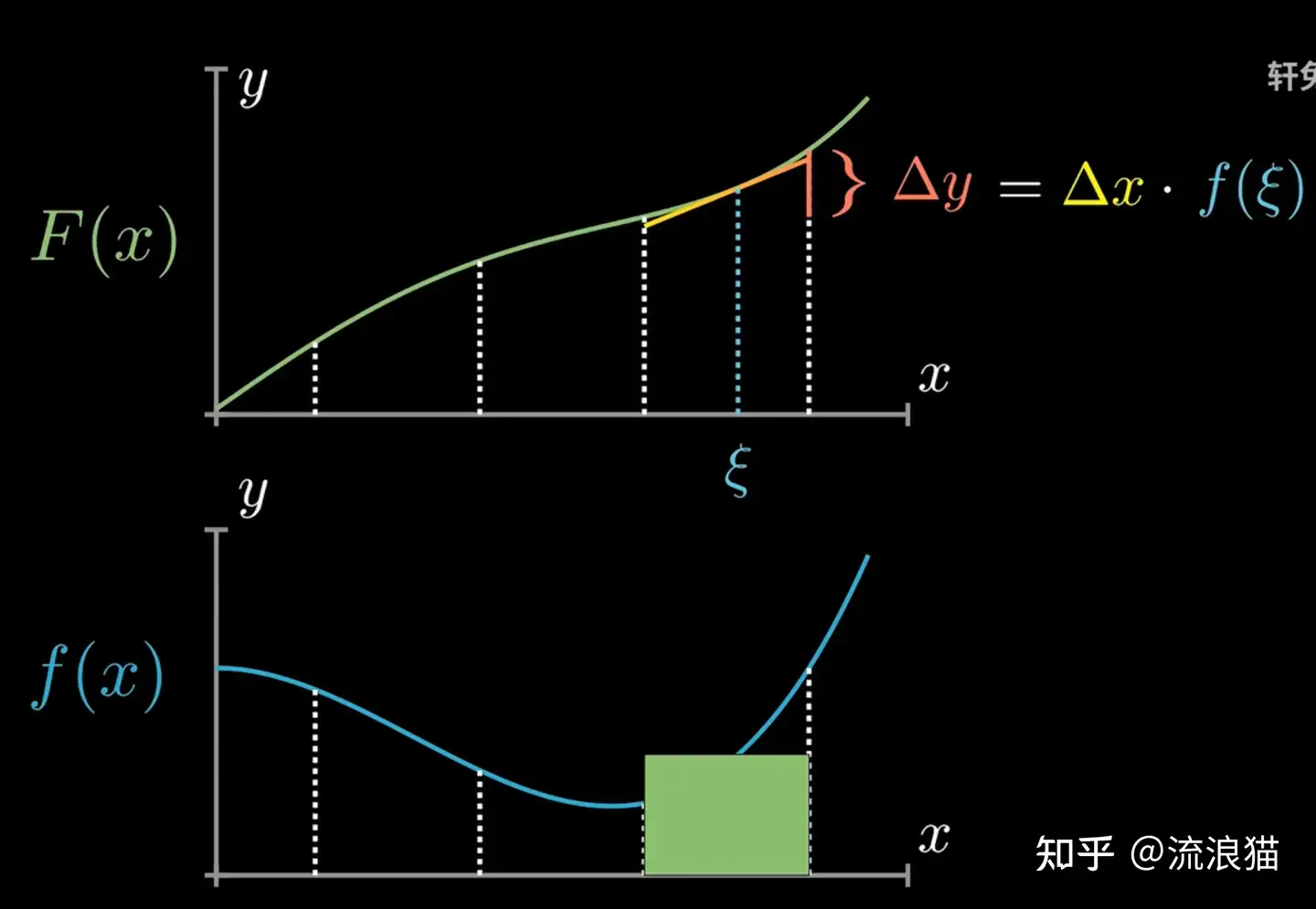


 浙公网安备 33010602011771号
浙公网安备 33010602011771号