Neural Network
逻辑回归用神经网络节点的方式表示
前面已经介绍过逻辑回归的模型,样本为(x,y) 其中y的值为1或0,假设x有2个特征,则对应关系如下图所示。
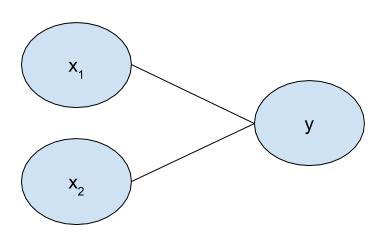 

实际情况是需要求需要三个参数,因此输入层需要添加一个节点表示偏置项。通过此模型对于任何一个输入x,都会产生一个输出与之对应。
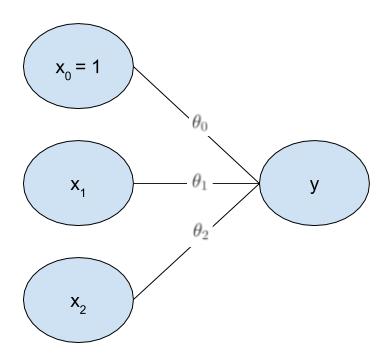 

有了这个图就可以方便的介绍神经网络模型了。
神经网络模型和参数
下图所示的是一个简单的神经网络模型和加入偏置项的示意图,输入和输出完全相同。区别是,比起逻辑回归它多了两个节点的隐藏层。通过分解可以发现它是由3个逻辑回归组成,按下图出现的顺序命名为LR01,LR02,LR03。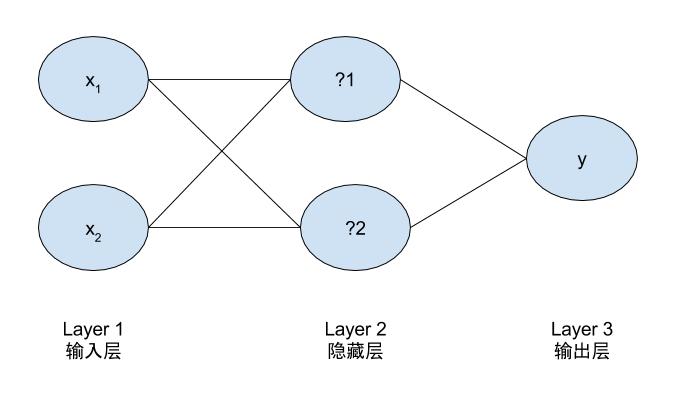 

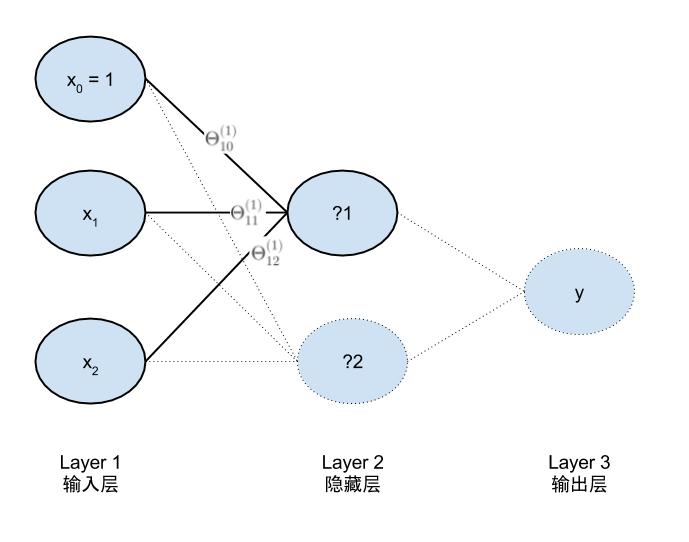 

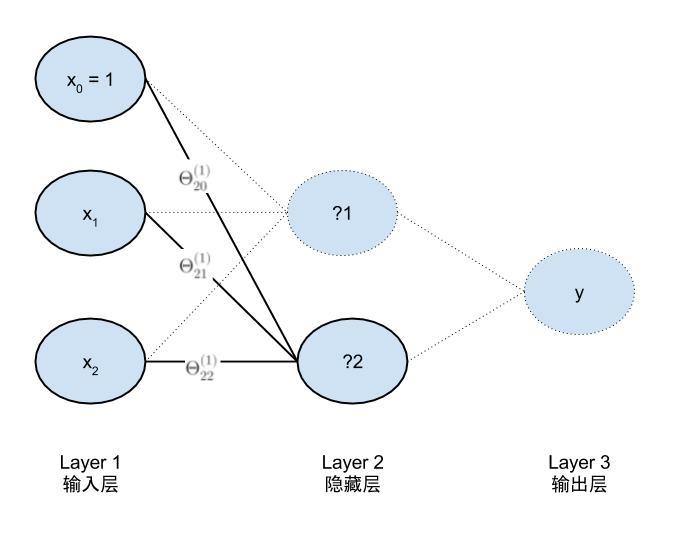 

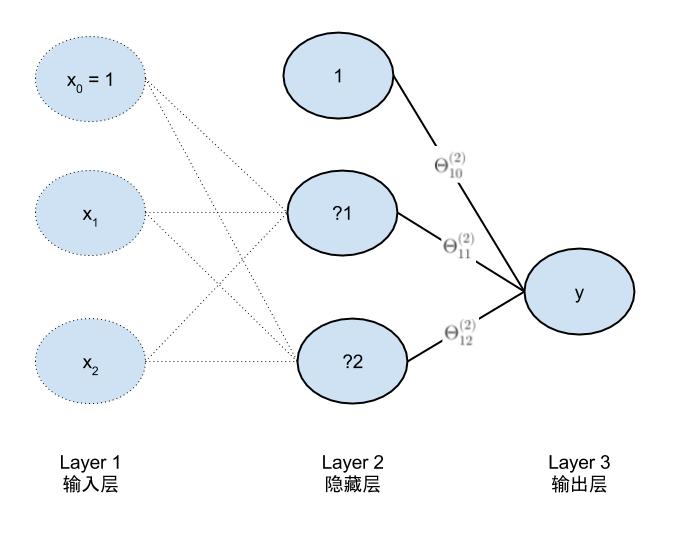 

完整的参数模型是
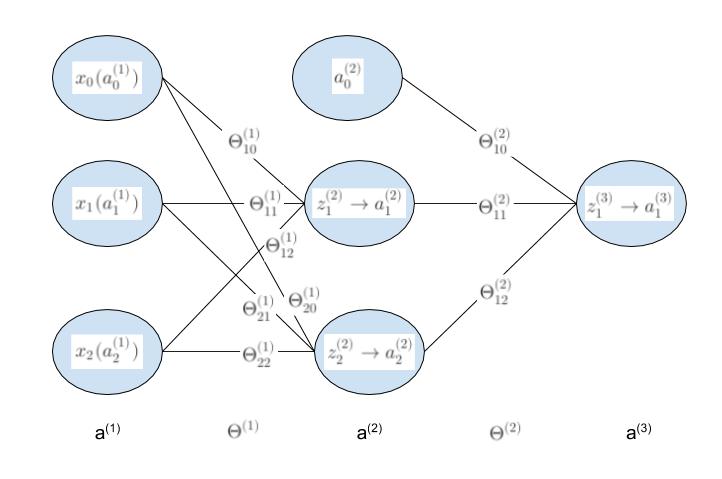 

a1为输入层输入值,即为x的值为LR01,LR02的输入。a2为LR03的输入 a3为最终的输出值。z2为一到二的中间值,z3为二到三层的中间值。
前向传播计算cost function
模型需要确定的参数个数为9个。由逻辑回归可知,对于LR01有
\[z_1^{(2)}=\Theta_{10}^{(1)}*a_0^{(1)}+\Theta_{11}^{(1)}*a_1^{(1)}+\Theta_{12}^{(1)}*a_2^{(1)}\]
\[a_1^{(2)}=\frac 1 {1+e^{-z_1^{(2)}}}\]
对于LR02有
\[z_2^{(2)}=\Theta_{20}^{(1)}*a_0^{(1)}+\Theta_{21}^{(1)}*a_1^{(1)}+\Theta_{22}^{(1)}*a_2^{(1)}\]
\[a_2^{(2)}=\frac 1 {1+e^{-z_2^{(2)}}}\]
LR01和LR02用矩阵描述如下
\[\Theta^{(1)}*a^{(1)}=z^{(2)}\]
其中
\[a^{(1)}=
\begin{pmatrix}
a_0^{(1)} \\
a_1^{(1)} \\
a_2^{(1)} \\
\end{pmatrix}
\]
\[\Theta^{(1)}=
\begin{pmatrix}
\Theta_{10}^{(1)} & \Theta_{11}^{(1)} & \Theta_{12}^{(1)} \\
\Theta_{20}^{(1)} & \Theta_{21}^{(1)} & \Theta_{22}^{(1)} \\
\end{pmatrix}
\]
\[z^{(2)}=
\begin{pmatrix}
z_1^{(2)} \\
z_2^{(2)} \\
\end{pmatrix}
\]
第二层到第三层,首先需要加入偏置节点a2_0然后第三层中间值和输出值为。
\[z_1^{(3)}=\Theta_{10}^{(2)}*a_0^{(2)}+\Theta_{11}^{(2)}*a_1^{(2)}+\Theta_{12}^{(2)}*a_2^{(2)}\]
\[a_1^{(3)}=\frac 1 {1+e^{-z_1^{(3)}}}\]
那么最终的损失函数为
\[J(\Theta)=-\frac 1 m[\sum_{i=1}^my^{(i)}log(a_1^{(3)})^{(i)}+(1-y^{(i)})log(1-(a_1^{(3)})^{(i)})]\]
下一步需要做的是使用梯度下降的方法求出所有的参数值。
反向传播计算梯度下降
对于每个参数\(\Theta^{(l)}_{ij}\)需要计算\(\frac{\partial J(\Theta)}{\partial \Theta^{(l)}_{ij}}\),计算公式如下。
\[\frac{\partial J(\Theta)}{\partial \Theta^{(2)}}=a^{(2)}\delta^{(3)}\]
\[\delta^{(3)}=(a^{(3)}_1-y).*g^{'}(z^{(3)})=(a^{(3)}_1-y)a^{(3)}(1-a^{(3)})\]
\[\frac{\partial J(\Theta)}{\partial \Theta^{(1)}}=a^{(1)}\delta^{(2)}\]
\[\delta^{(2)}=(\Theta^{(2)})^T\delta^{(3)}.*g^{'}(z^{(2)})=(\Theta^{(2)})^T\delta^{(3)}a^{(2)}(1-a^{(2)})\]
示例一共有9个参数,现在只需要推导出4个。使用的是求导的链式法则。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号