[NOI2019]序列 题解

同步赛当场降智了，认为贪心是假的。。。。然后。。。。就写了个暴力。。。。

开题一看，这不是模拟费用流吗？

然而这个费用流并不显然。。。。所以我当时放弃了T3部分分没想到。

当然也希望这个题解能让大家懂得什么是真正的模拟费用流啦

Part1:费用流

大概是这么一张图……

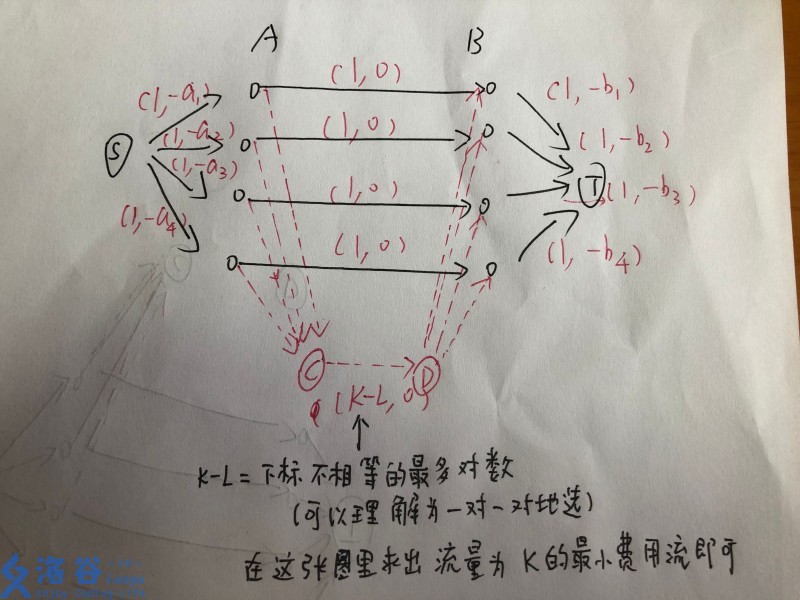
正确性嘛……就是如果选下标不同的一对数的话必须走\(C -> D\) 这条路径

那么就保证了下标不同的数的对数会\(<= K - L\),那么相同的就至少有\(L\)对了。

然后你按上述方法建图，写个费用流就可以拿到\(n = 150\)或者\(n = 2000\)的分了。

Part2:贪心(模拟费用流)

考虑一点一点的增加流量。

如果弧\(CD\)没有流满，我们就流弧\(CD\)，因为它的选择最“自由”，得到的答案也最优。

怎么流最优呢？当然是当前没有被选中的数中，A/B各取一个max

当然如果我们选的数中有下标相等的，就不用占据弧CD的流量了，这个需要注意。

在弧\(CD\)流满之后，我们考虑增加其他弧的流量，也就是要组成新的一对下标相等的数

首先我们可以直接找一个AB都没被选过的下标，选出一个\(A_i+B_i\) 最大的，反映到图上就是把 \(S->A_i ->B_i ->T\) 流一遍

我们还可以给一个已经选中的\(A\)找一个\(B\)和它配对，然后你会发现这会使得\(C\)少一点流量，所以我们要给\(C\)一点流量，不然就不满足流量平衡了

所以我们还得再找一个最大的没选过的\(A\)……

同样的我也可以给一个没配过对的\(B\)配对，再补一个最大的\(B\)上去……

反映到图上，就是把一条\(A_i->C\)的流量撤回，改为从\(A_i->B_i->T\)

然后换一个\(A_j\)补上，流一下\(S - >A_j - >C\)这条边。

过程中如果发现弧CD可以不流满，比如上述配对的过程中如果配出了两对的话，我们就在剩下的A和B中分别选取一个最大值，保证CD流满。

这个就是一些人的贪心……在此处orz@_rqy提供的贪心思路……

不过我把它用费用流的角度解释的话……它就是模拟费用流呀！

所以这个贪心（模拟费用流）是正确的！

Part3：代码

然后我们发现我们只要求一个最大值……用堆维护就可以了……

(代码行数有点多，勿喷)

代码里有详细注释~~~

// F1,F2表示可以用来做配对操作的堆，H1，H2表示A、B两个数组中剩余的数
// H3存的是A、B都没选的那些i(也是堆)
#include <bits/stdc++.h>
#define LL long long
using namespace std;
inline int read(){
    static int x; x = 0; static char c; c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = x * 10 + c - '0',c = getchar();
    return x;
}
inline void write(LL x){ if (x > 9) write(x/10); putchar(x%10+'0'); }
inline void writeln(LL x){ write(x),putchar('\n'); }

const int N = 1000050;
LL ans;
int T,n,L,K,a[N],b[N],s[N]; // 0 -> () 1 -> (a) 2 -> (b) 3 -> (ab)

int id[N];
inline bool cmpa(int x,int y){ return a[x] > a[y]; }
inline bool cmpb(int x,int y){ return b[x] > b[y]; }
inline void work(int m){
	ans = 0;
	static int i; 
	for (i = 1; i <= n; ++i) id[i] = i;
	sort(id+1,id+n+1,cmpa); for (i = 1; i <= m; ++i) ++s[id[i]],ans += a[id[i]];
	sort(id+1,id+n+1,cmpb); for (i = 1; i <= m; ++i) s[id[i]] += 2,ans += b[id[i]];
}

struct NodeA{ int id; bool operator < (const NodeA x) const{ return a[id] < a[x.id]; } }tmp1;
struct NodeB{ int id; bool operator < (const NodeB x) const{ return b[id] < b[x.id]; } }tmp2;
struct NodeAB{ int id; bool operator < (const NodeAB x) const{ return a[id] + b[id] < a[x.id] + b[x.id]; } }tmp3;
priority_queue<NodeA>H1,F1;
priority_queue<NodeB>H2,F2;
priority_queue<NodeAB>H3;

int main(){
	LL v1,v2,v3,vmx;
	int i,j,now,c1,c2;
	T = read();
	while (T--){
		n = read(),K = read(),L = read();
		for (i = 1; i <= n; ++i) a[i] = read();
		for (i = 1; i <= n; ++i) b[i] = read(),s[i] = 0;
		work(K-L); //实际操作中我并没有选择流满CD，只是先流K-L
		
		while (!H1.empty()) H1.pop();
		while (!F1.empty()) F1.pop();
		while (!H2.empty()) H2.pop();
		while (!F2.empty()) F2.pop();
		while (!H3.empty()) H3.pop();
		now = 0;
		for (i = 1; i <= n; ++i){
			if (!s[i]){
				tmp1.id = i,H1.push(tmp1);
				tmp2.id = i,H2.push(tmp2);
				tmp3.id = i,H3.push(tmp3);
			}
			else if (s[i] == 1) tmp2.id = i,H2.push(tmp2),F2.push(tmp2);
			else if (s[i] == 2) tmp1.id = i,H1.push(tmp1),F1.push(tmp1);
			else ++now;
        //A、B都选了的，我会计到now中去，now表示CD弧剩余的流量。
		}
		
		while (L--){ //每次增加一点流量
			while (!H1.empty() && (s[H1.top().id] & 1)) H1.pop();
			while (!F1.empty() && (s[F1.top().id] ^ 2)) F1.pop();
			while (!H2.empty() && (s[H2.top().id] & 2)) H2.pop();
			while (!F2.empty() && (s[F2.top().id] ^ 1)) F2.pop();
			while (!H3.empty() && s[H3.top().id]) H3.pop();
			
			if (now){ //如果CD弧有流量，就选两个最大值
				--now;
				i = H1.top().id,j = H2.top().id;
				ans += a[i] + b[j];
				s[i] |= 1,s[j] |= 2;
				if (s[i] ^ 3) tmp2.id = i,F2.push(tmp2);
				if (s[j] ^ 3) tmp1.id = j,F1.push(tmp1); 
				
				if (i == j) ++now;
				else{
					if (s[i] == 3) ++now; 
					if (s[j] == 3) ++now; 
				}
				continue;
			}
			
			v1 = v2 = v3 = c1 = c2 = 0;
			if (!F2.empty()){ //给B配对
				i = H1.top().id,j = F2.top().id; v1 = a[i] + b[j]; c1 = s[i] != 2 ? 1 : 0;
			}
			if (!F1.empty()){ //给A配对
				i = F1.top().id,j = H2.top().id; v2 = a[i] + b[j]; c2 = s[j] != 3 ? 1 : 0;
			}
			if (!H3.empty()){ i = H3.top().id,v3 = a[i] + b[i]; } //选一对A+B
			vmx = max(v1,max(v2,v3));
			ans += vmx;
			
			
			if (v1 == v2 && v1 == vmx){ 
         //解释一下这个判断：
         //因为在费用相同时，给CD弧增加空余的流量是比较优的
         //所以我还比较了c1和c2(优先给CD弧增加空余流量)
				if (c1 >= c2){
					i = H1.top().id,j = F2.top().id;
					s[i] |= 1,s[j] |= 2;
					if (s[i] ^ 3) tmp2.id = i,F2.push(tmp2); else ++now;
				}
				else{
					i = F1.top().id,j = H2.top().id;
					s[i] |= 1,s[j] |= 2;
					if (s[j] ^ 3) tmp1.id = j,F1.push(tmp1); else ++now;					
				}
				continue;
			}
			if (v1 == vmx){
				i = H1.top().id,j = F2.top().id;
				s[i] |= 1,s[j] |= 2;
				if (s[i] ^ 3) tmp2.id = i,F2.push(tmp2); else ++now;
				continue;
			}
			if (v2 == vmx){
				i = F1.top().id,j = H2.top().id;
				s[i] |= 1,s[j] |= 2;
				if (s[j] ^ 3) tmp1.id = j,F1.push(tmp1); else ++now;
				continue;
			}
			if (v3 == vmx) {i = H3.top().id,H3.pop(),s[i] = 3; continue;}
		}
		
		writeln(ans);
	}
    return 0;
}