求最大公约数伪代码
1. 上网查找什么是求两个数的最大公约数的欧几里得算法(辗转相除法)
定理: 设a、b均为正整数,则gcd(a,b) = gcd(b, a%b)
证明: 设 a = kb + r, 其中k和r分别为a除以b得到的商和余数.
则有r = a - kb成立.
假设d是a、b的最大公约数.那么d也是r的一个约数.
即d是 b 和 a%b 的最大公约数.因此从左到右得证.
同理,由a = kb + r可证从右到左也成立.因此定理得证
- 当a < b时, 仅仅只是将a、b进行交换
- 当a > b时, 就可以使数据规模变小,并且变小的速度极快
递归边界: 如何确定递归边界呢?
首先我们知道0和任何一个数的最大公约数,都是那个数. 如0和6的最大公约数一定是6. 因此如果们发现出现了0这个数,那么就可以直接得出最大公约数.
https://blog.csdn.net/chenzengxun/article/details/97956408
2. 参考教材,用伪代码(英语或汉语)实现欧几里得算法(辗转相除法),提交伪代码。
取两个整数m,n(不妨m>=n)
用m关于n的模替换m
两个数中若其中一个为0那么最大公约数必然是另一个不为0的数
若两个数均不为0,则重复上述操作
3. 选择几组数据,手动走一下伪代码,测试你写的伪代码是否正确
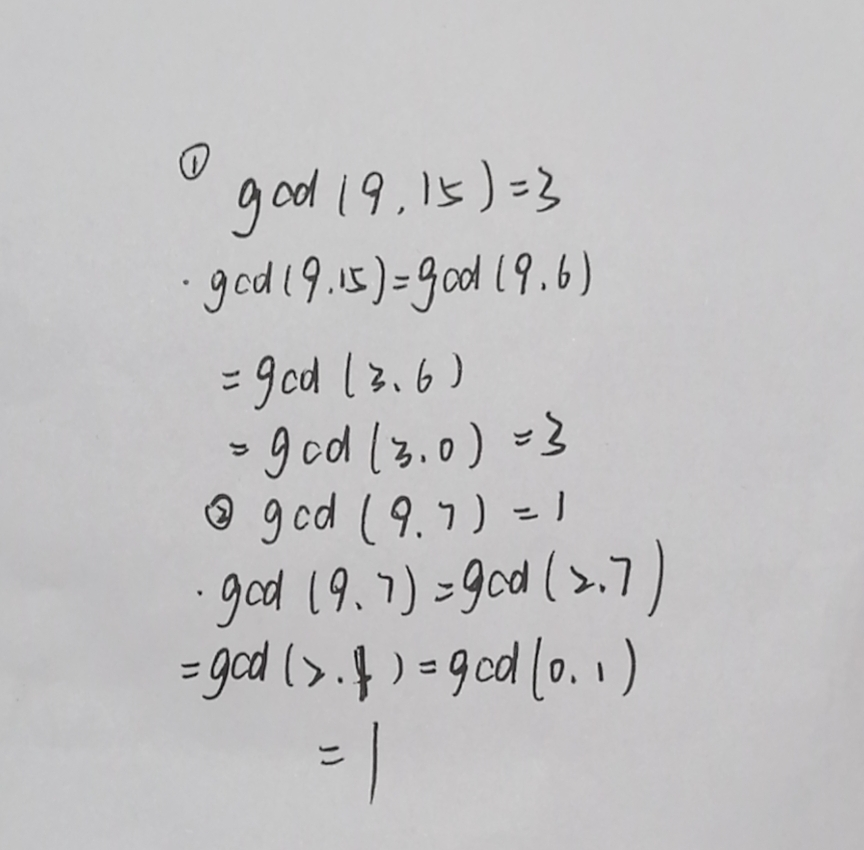



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识?