吃瓜教程|Datawhale-10月（2）

吃瓜教程|Datawhale-10月（2）

机器学习三要素

• 模型：根据具体问题，确定假设空间

• 策略：根据评价标准，确定选取最优模型的策略（通常会产生一个“损失函数”）

• 算法：求解损失函数，确定最优模型

线性模型

基本形式

给定由 \(d\) 个属性描述的实例 \(\boldsymbol{x}=(x_{1};x_{2};…;x_{d})\) ，其中 \(x_i\) 是 \(\boldsymbol{x}\) 在第i个属性上的取值，线性模型试图学得一个通过属性的线性组合来进行预测的函数，即：

\[f(\boldsymbol{x})=w_{1}x_{1}+w_{2}x_{2}+…+w_{d}x_{d}+b \]

用向量一般形式为：

\[f(\boldsymbol{x} )=\boldsymbol{w}^{T}\boldsymbol{x}+b \]

其中 \(\boldsymbol{w}=(w_{1};w_{2};…;w_{d})\) ， \(\boldsymbol{w}\) 和 \(b\) 学得之后，模型就可以确定。

线性回归

一元线性回归

试图学得一个线性模型以尽可能准确地预测实值输出标记。即：

\[f(x_{i})=wx_{i}+b,使得f(x_{i})\simeq y_{i} \]

其中， \(w\) 和 \(b\) 的确定关键在于如何衡量 \(f(x_{i})\) 和 \(y\) 之间的差别。这里使用了均方误差（回归任务中最常见的性能度量），即：

\[\begin{aligned} (w^{*},b^{*}) & = \mathop{\arg\min}\limits_{(w,b)}\sum_{i=1}^{m} (f(x_{i})-y_{i})\\ & = \mathop{\arg\min}\limits_{(w,b)}\sum_{i=1}^{m} (y_{i}-wx_{i}-b) \end{aligned} \]

其中， \(\mathop{\arg\min}\limits_{(w,b)}\) 指当后边部分最小时，w和b的取值。

均方误差对应了“欧氏距离”，基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。在线性回归中即为：

• 试图找到一条直线使所有样本到直线上的欧氏距离之和最小。

线性回归模型的最小二乘“参数估计”：

• 求解 \(w\) 和 \(b\) 使 \(E_{(w,b)}={\textstyle \sum_{i=1}^{m}}(y_{i}-wx_{i}-b)^{2}\) 最小化

求解 \(w\) 和 \(b\) 其本质是一个多元函数求最值（点）的问题

（求导）即：

\[\frac{\partial E(w,b)}{\partial w}=2(w\sum_{i=1}^{m} x_{i}^{2}-\sum_{i=1}^{m} (y_{i}-b)x_{i}) \]

\[\frac{\partial E(w,b)}{\partial b}=2(mb-\sum_{i=1}^{m} (y_{i}-wx_{i})) \]

将上述两式=0可得：（具体推导见南瓜书）

\[w = \frac{\sum_{i=1}^{m} y_{i}(x_{i}-\bar{x} )}{\sum _{i=1}^{m}x_{i}^{2}-\frac{1}{2}(\sum_{i=1}^{m}x_{i} )^{2} } \]

\[b = \frac{1}{m}\sum_{i=1}^{m} (y_{i}-wx_{i}) \]

多元线性回归

对于 基本形式 中的 \(f(\boldsymbol{x} )=\boldsymbol{w}^{T}\boldsymbol{x}+b\) 使得 \(f(\boldsymbol{x}_{i})\simeq y_{i}\) ，称为多元线性回归。

把 \(w\) 和 \(b\) 用 \(\hat{\boldsymbol{w}}=(\boldsymbol{w};b)\) 表示，数据集D用 m x (d+1) 的矩阵 $\mathbf{X} $ 表示，其中每行对应一个示例，该行前d个元素对应于d个属性，最后一位=1。即：

\[\mathbf{X} =\begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1\\ x_{21} & x_{22} & \cdots & x_{2d} & 1\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ x_{m1} & x_{m2} & \cdots & x_{md} & 1\\ \end{pmatrix} =\begin{pmatrix} x_{1}^{T} & 1\\ x_{2}^{T} & 1\\ \vdots & \vdots\\ x_{m}^{T} & 1\\ \end{pmatrix} \]

令 \(\boldsymbol{y}=(y_{1};y_{2};...;y_{m})\) 则有：

\[\hat{\boldsymbol{w}}^{*}=\underset{\hat{\boldsymbol{w}}}{\arg \min }(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}}) \]

令 \(E_{\hat{\boldsymbol{w}}}=(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})\) ，对 \(\hat{\boldsymbol{w}}\) 求导得：

\[\frac{\partial E_{\hat{\boldsymbol{w}}}}{\partial \hat{\boldsymbol{w}}}=2 \mathbf{X}^{\mathrm{T}}(\mathbf{X} \hat{\boldsymbol{w}}-\boldsymbol{y}) \]

当 \(\mathbf{X}^{T}\mathbf{X}\) 为满秩矩阵或者正定矩阵时，令上式 = 0可得：

\[\hat{\boldsymbol{w}}^{*}=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\boldsymbol{y} \]

令 \(\hat{\boldsymbol{x}}_{i}=(\boldsymbol{x}_{i};1)\) ，最终学得的多元线性回归模型为：

\[f(\hat{\boldsymbol{x}}_{i})=\hat{\boldsymbol{x}}_{i}^{T}(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\boldsymbol{y} \]

当 \(\mathbf{X}^{T}\mathbf{X}\) 不为满秩矩阵或者正定矩阵时，可解出多个 \(\hat{\boldsymbol{w}}\) ，此时选择哪个作为输出就由学习算法的归纳偏好决定，常见做法就是引入正则化项。

对数几率回归

其实是解决分类问题，在线性模型的基础上套一个映射函数来实现分类功能

对于二分类

我们需要正例的概率P（反例的概率为1-P），该概率P∈[0.1]。但是线性回归中的预则值 f(x) ∈ R ，所以要套一个映射函数（对数几率函数） \(y=\frac{1}{1-e^{-z}}\) 来使最终结果控制在[0.1]。其中 z 为 f(x) 。

则有：

\[y=\frac{1}{1-e^{-(\boldsymbol{w}^{T}\boldsymbol{x}+b)}} \]

最终变换为：

\[\ln{\frac{y}{1-y}}=\boldsymbol{w}^{T}\boldsymbol{x}+b \]

其中 \(y\) 视为 \(p(y=1 | \boldsymbol{x})\) 则 \(1-y\) 为 \(p(y=0 | \boldsymbol{x})\) ，即：

\[\ln{\frac{p(y=1 | \boldsymbol{x})}{p(y=0 | \boldsymbol{x})}}=\boldsymbol{w}^{T}\boldsymbol{x}+b \]

可以推导出：

\[p(y=1 | \boldsymbol{x}) =\frac{e^{\boldsymbol{w}^{T}\boldsymbol{x}+b}}{1+e^{\boldsymbol{w}^{T}\boldsymbol{x}+b}} \]

\[p(y=0 | \boldsymbol{x}) =\frac{1}{1+e^{\boldsymbol{w}^{T}\boldsymbol{x}+b}} \]

为了方便讨论，令 \(\beta =(\boldsymbol{w};b),\hat{\boldsymbol{x}}=(\boldsymbol{x};1)\) 则上式可简写为：

\[p(y=1 | \boldsymbol{x}) =\frac{e^{\beta^{T}\hat{\boldsymbol{x}}}}{1+e^{\beta^{T}\hat{\boldsymbol{x}}}}=p_{1}(\hat{\boldsymbol{x}};\beta) \]

\[p(y=0 | \boldsymbol{x}) =\frac{1}{1+e^{\beta^{T}\hat{\boldsymbol{x}}}}=p_{0}(\hat{\boldsymbol{x}};\beta) \]

故 \(y\in \{0,1\}\) 的概率质量函数为：

\[p(y|\hat{\boldsymbol{x}};\beta)=y\cdot p_{1}(\hat{\boldsymbol{x}};\beta)+(1-y)\cdot p_{0}(\hat{\boldsymbol{x}};\beta) \]

*当 y = 1 时 \(p(y|\hat{\boldsymbol{x}};\beta)=p_{1}(\hat{\boldsymbol{x}};\beta)\) ，当 y = 0 时 \(p(y|\hat{\boldsymbol{x}};\beta)=p_{0}(\hat{\boldsymbol{x}};\beta)\)

对率回归模型得最大化“对数似然”：

\[\ell(\boldsymbol{\beta})=\sum_{i=1}^{m} \ln p(y_{i}|\hat{\boldsymbol{x}};\beta) \]

带入得：

\[\ell(\boldsymbol{\beta})=\sum_{i=1}^{m}\left(-y_{i} \boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_{i}+\ln \left(1+e^{\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_i}\right)\right)\tag{1} \]

*根据南瓜书好推导一点

该式子为关于 \(\beta\) 的高阶可导连续凸函数。可以用梯度下降和牛顿法求得最优解。

下边是求得式（1）的两种方法的相关知识

最大似然估计

一文搞懂极大似然估计

对于这个函数 \(p(x|\theta)\) ： 输入有两个：x 表示某一个具体的数据； \(\theta\) 表示模型的参数

如果 \(\theta\) 是已知确定的，x 是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点 x，其出现概率是多少。

如果是已知确定的 x， \(\theta\) 是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现 x 这个样本点的概率是多少。让这个概率最大化就是最大似然估计。

最大似然估计你可以把它看作是一个反推。多数情况下我们是根据已知条件来推算结果，而最大似然估计是已经知道了结果，然后寻求使该结果出现的可能性最大的条件，以此作为估计值。

求最大似然函数估计值的一般步骤：

（1）写出似然函数；

（2）对似然函数取对数，并整理；

（3）求导数，令导数为0，得到似然方程；

（4）解似然方程，得到的参数即为所求；^[1]

信息论

以概率论、随机过程为基本研究工具，研究广义通信系统的整个过程。

自信息

\[I(X)=-\log _{b} p(x) \]

当 b = 2 时单位为 bit ，当 b = e 时单位为 nat

信息熵（自信息的期望）

度量随机变量 X 的不确定性，信息熵越大越不确定。

相对熵（KL散度）

度量两个分布的差异，其典型使用场景是用来度量理想分布 p(x) 和模拟分布 q(x) 之间的差异。

\[\begin{aligned} D_{K L}(p \| q) &=\sum_{x} p(x) \log _{b}\left(\frac{p(x)}{q(x)}\right) \\ &=\sum_{x} p(x)\left(\log _{b} p(x)-\log _{b} q(x)\right) \\ &=\sum_{x} p(x) \log _{b} p(x)-\sum_{x} p(x) \log _{b} q(x) \end{aligned} \]

其中 \(-\sum_{x} p(x) \log _{b} q(x)\) 称为交叉熵

与理想分布最接近的模拟分布为最优分布，可以通过最小化相对熵来求出，即最小化交叉熵。

对数几率回归的机器学习三要素

• 模型：线性模型，输出值范围 [0,1] ，近似阶跃的单调可微函数

• 策略：极大似然估计，信息论

• 算法：梯度下降，牛顿法

线性判别分析

线性判别分析（LDA）思想：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异类样例的投影点尽可能远离。

几何角度：全体训练样本经过投影后

• 异类样本的中心尽可能远
• 同类样本的方差尽可能小

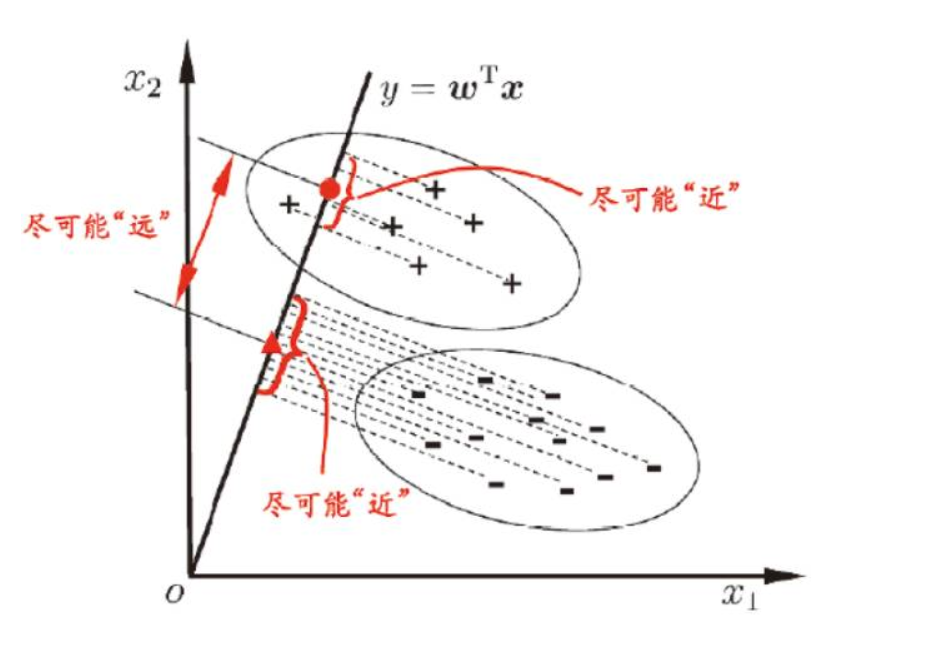
给定数据集 \(D=\{(x_{i},y_{i})\}_{i=1}^{m},y\in \{0,1\}\) ，令 \(X_{i}、\mu _{i}、\Sigma _{i}\) 分别表示 \(i\in \{0,1\}\) （这三个的下标i指的是0或1，数据集中的下标i表示的是样本编号）类示例的集合、均值向量、协方差矩阵。若将数据投影到直线 \(w\) 上，则两类样本的中心在直线上的投影（非严格）分别为 \(w^{T}\mu _{0}\) 和 \(w^{T}\mu _{1}\) ；若将所有样本点都投影到直线上，则两类样本的协方差分别为 \(w^{T}\Sigma _{0}w\) 和 \(w^{T}\Sigma _{1}w\) 。由于直线是一维空间，因此上述四个为实数。

• \(w^{T}\mu _{0}=|\boldsymbol{w}| \cdot\left|\boldsymbol{\mu}_{0}\right| \cdot \cos \theta_{0}，其中 \left|\boldsymbol{\mu}_{0}\right| \cdot \cos \theta_{0}为投影\)

故异类样本的中心尽可能远（非严格投影）为：

\[\max \left\|w^{T}\mu _{0}-w^{T}\mu _{1}\right\|_{2}^{2} \]

\[\max \left\||\boldsymbol{w}| \cdot\left|\boldsymbol{\mu}_{0}\right| \cdot \cos \theta_{0}-|\boldsymbol{w}| \cdot\left|\boldsymbol{\mu}_{1}\right| \cdot \cos \theta_{1}\right\|_{2}^{2} \]

同类样本的方差尽可能小（非严格方差）为：

\[\min\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\Sigma}_{0} \boldsymbol{w} \]

\[\begin{aligned} \boldsymbol{w}^{\mathrm{T}} \boldsymbol{\Sigma}_{0} \boldsymbol{w} &=\boldsymbol{w}^{\mathrm{T}}\left(\sum_{\boldsymbol{x} \in X_{0}}\left(\boldsymbol{x}-\boldsymbol{\mu}_{0}\right)\left(\boldsymbol{x}-\boldsymbol{\mu}_{0}\right)^{\mathrm{T}}\right) \boldsymbol{w} \\ &=\sum_{\boldsymbol{x} \in X_{0}}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\mu}_{0}\right)\left(\boldsymbol{x}^{\mathrm{T}} \boldsymbol{w}-\boldsymbol{\mu}_{0}^{\mathrm{T}} \boldsymbol{w}\right) \end{aligned} \]

其中 \(w^{T}x\) 为样本 \(w^{T}\mu_{0}\) 为中心。

同时考虑上述两个条件，则得：

\[\begin{aligned} \max J &=\frac{\left\|\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\mu}_{0}-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\mu}_{1}\right\|_{2}^{2}}{\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\Sigma}_{0} \boldsymbol{w}+\boldsymbol{w}^{\mathrm{T}} \boldsymbol{\Sigma}_{1} \boldsymbol{w}}\\ &=\frac{\boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{\mu}_{0}-\boldsymbol{\mu}_{1}\right)\left(\boldsymbol{\mu}_{0}-\boldsymbol{\mu}_{1}\right)^{\mathrm{T}} \boldsymbol{w}}{\boldsymbol{w}^{\mathrm{T}}\left(\boldsymbol{\Sigma}_{0}+\boldsymbol{\Sigma}_{1}\right) \boldsymbol{w}} \end{aligned} \]

将 \(\left(\boldsymbol{\mu}_{0}-\boldsymbol{\mu}_{1}\right)\left(\boldsymbol{\mu}_{0}-\boldsymbol{\mu}_{1}\right)^{T}\) 记作 \(S_{b}\) （类间散度矩阵）， \(\boldsymbol{\Sigma}_{0}+\boldsymbol{\Sigma}_{1}\) 记作 \(S_{w}\) （类内散度矩阵），则上式可写为：

\[\max J=\frac{\boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{b} \boldsymbol{w}}{\boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{w} \boldsymbol{w}} \]

即 \(S_{b}和S_{w}\) 的广义瑞利商。

上式中 \(w\) 不会影响结果，所以将分母进行固定，令 \(\boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{w} \boldsymbol{w}=1\) （这里固定其他含 \(w\) 的项都可以），得：

\[\begin{array}{ll} \min _{w} & -\boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{b} \boldsymbol{w} \\ \text { s.t. } & \boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{w} \boldsymbol{w}=1 \end{array} \]

根据拉格朗日乘子法，该式等价于：

\[\begin{array}{c} \mathbf{S}_{b} \boldsymbol{w}=\lambda \mathbf{S}_{w} \boldsymbol{w} \\ \left(\boldsymbol{\mu}_{0}-\boldsymbol{\mu}_{1}\right)\left(\boldsymbol{\mu}_{0}-\boldsymbol{\mu}_{1}\right)^{\mathrm{T}} \boldsymbol{w}=\lambda \mathbf{S}_{w} \boldsymbol{w} \end{array} \]

若令 \(\left(\boldsymbol{\mu}_{0}-\boldsymbol{\mu}_{1}\right)\left(\boldsymbol{\mu}_{0}-\boldsymbol{\mu}_{1}\right)^{\mathrm{T}} \boldsymbol{w}=\gamma\) ，则

\[\begin{array}{l} \gamma\left(\boldsymbol{\mu}_{0}-\boldsymbol{\mu}_{1}\right)=\lambda \mathbf{S}_{w} \boldsymbol{w} \\ \boldsymbol{w}=\frac{\gamma}{\lambda} \mathbf{S}_{w}^{-1}\left(\boldsymbol{\mu}_{0}-\boldsymbol{\mu}_{1}\right) \end{array} \]

因为最终求解的 \(w\) 不关心其大小，只关心其方向，所以 $\frac{\gamma}{\lambda} $ 可以取任意值，若令其等于1，则：

\[\boldsymbol{w}=\mathbf{S}_{w}^{-1}\left(\boldsymbol{\mu}_{0}-\boldsymbol{\mu}_{1}\right) \]

协方差

\[\sigma(x, y)=\frac{1}{n-1} \sum_{a}^{b}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right) \]

前边的系数可以省略，即：

\[\sigma(x, y)=\sum_{a}^{b}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right) \]

范数

• 一范数：所有元素绝对值的和 \(||x||_{1}\)

• 二范数：向量的模长 \(||x||_{2}\)

• 无穷范数：

  • 正无穷范数：所有元素中绝对值最小的。 \(||x||_{+\infty }=\min(|x_1|...|x_{n}|)\)
  • 负无穷范数：所有元素中绝对值最大的。\(||x||_{-\infty }=\max(|x_1|...|x_{n}|)\)

拉格朗日乘子法

对于仅含等式约束的优化问题：（max问题可以通过加“-”号变为min问题）

\[\begin{array}{cl} \min _{x} & f(\boldsymbol{x}) \\ \text { s.t. } & h_{i}(\boldsymbol{x})=0 \quad i=1,2, \ldots, n \end{array} \]

其中 \(\boldsymbol{x} \in \mathbb{R}^{n}, f(\boldsymbol{x}) \text { 和 } h_{i}(\boldsymbol{x})\) 均有连续地一阶偏导数。首先列出其拉格朗日函数：

\[L(\boldsymbol{x}, \boldsymbol{\lambda})=f(\boldsymbol{x})+\sum_{i=1}^{n} \lambda_{i} h_{i}(\boldsymbol{x}) \]

其中 $ \boldsymbol{\lambda}=\left(\lambda_{1}, \lambda_{2}, \ldots, \lambda_{n}\right)^{\mathrm{T}}$ 为拉格朗日乘子。然后对拉格朗日函数关于 \(\boldsymbol{x}\) 求偏导, 并令导数等于0再搭配约束条件 \(h_{i}(\boldsymbol{x})=0\) 解出 \(\boldsymbol{x}\) , 求解出的所有 \(\boldsymbol{x}\) 即为上述优化问题的所有 可能【极值点】

广义特征值

设 \(\mathbf{A}, \mathbf{B}\) 为n阶方阵, 若存在数 \(\lambda\) ，使得方程 \(A \boldsymbol{x}=\lambda \mathbf{B} \boldsymbol{x}\) 存在非零解, 则称 \(\lambda\) 为 \(\mathbf{A}\) 相对于 \(\mathbf{B}\) 的广义特征值， \(\boldsymbol{x}\) 为 \(\mathbf{A}\) 相对于 \(\mathbf{B}\) 的属于广义特征值 \(\lambda\) 的特征向量。特别地, 当 \(\mathbf{B}=\mathbf{I}\) (单位矩阵）时, 广义特征值问题退化为标准特征值问题。

广义瑞利商

设 \(\mathbf{A}, \mathbf{B}\) 为n阶厄米（Hermitian）矩阵（转置之后是其本身，叫实对称矩阵。Hermitian矩阵是实对称矩阵的推广，共轭转置等于本身的矩阵），且 \(\mathbf{B}\) 正定，称 \(R(\boldsymbol{x})=\frac{\boldsymbol{x}^{\mathrm{H}} \mathbf{A} \boldsymbol{x}}{\boldsymbol{x}^{\mathrm{H}} \mathbf{B} \boldsymbol{x}}(\boldsymbol{x} \neq \mathbf{0})\) 为 \(\mathbf{A}\) 相对于 \(\mathbf{B}\) 的广义瑞利商。特别地，当 \(\mathbf{B}=\mathbf{I}\) (单位矩阵）时，广义瑞利商退化为瑞利商。

广义瑞利商的性质

设 \(\lambda_{i}, \boldsymbol{x}_{i}(i=1,2, \ldots, n)\) 为 \(\mathbf{A}\) 相对于 \(\mathbf{B}\) 的广义特征值和特征向量, 且 $\lambda_{1} \leqslant \lambda_{2} \leqslant \ldots \leqslant \lambda_{n} $ 。

\[\begin{array}{l} \min _{\boldsymbol{x} \neq 0} R(\boldsymbol{x})=\frac{\boldsymbol{x}^{\mathrm{H}} \mathbf{A} \boldsymbol{x}}{\boldsymbol{x}^{\mathrm{H}} \mathbf{B} \boldsymbol{x}}=\lambda_{1}, \boldsymbol{x}^{*}=\boldsymbol{x}_{1} \\ \max _{\boldsymbol{x} \neq 0} R(\boldsymbol{x})=\frac{\boldsymbol{x}^{\mathrm{H}} \mathbf{A} \boldsymbol{x}}{\boldsymbol{x}^{\mathrm{H}} \mathbf{B} \boldsymbol{x}}=\lambda_{n}, \boldsymbol{x}^{*}=\boldsymbol{x}_{n} \end{array} \]

【证明】：当固定 \(\boldsymbol{x}^{\mathrm{H}} \mathbf{B} \boldsymbol{x}=1\) 时，使用拉格朗日乘子法可推得 \(\mathbf{A} \boldsymbol{x}=\lambda \mathbf{B} \boldsymbol{x}\) 这样一个广 义特征值问题, 因此 \(\boldsymbol{x}\) 所有可能的解即为 \(\boldsymbol{x}_{i}(i=1,2, \ldots, n)\) 这 n个广义特征向量, 将其分别代入 \(R(\boldsymbol{x})\) 即可推得上述结论。

---

1. https://blog.csdn.net/zouxy09/article/details/8537620 ↩︎