[机器学习] 直观理解PCA

PCA（Principal Component Analysis，主元分析）是一种对数据进行分析的技术，可以去除数据中的噪音或冗余，实现将复杂数据降维的效果。

本文的案例主要来自参考资料1、2，原理推导来自参考资料1。本文的线性代数基变换部分建议结合参考资料3的视频观看，强推3Blue1Brown大神的系列教程。

0 引例-弹簧运动规律实验

0.1 实验设置

想象这样一个场景，我们想研究理想弹簧的运动规律。为此，我们构建了如下图1所示的测定实验。假设图中的球连接在一个无质量、无摩擦的弹簧之上，从平衡位置沿x轴拉开一定的距离然后释放。
我们在不同角度放置了三个摄像机，每个摄像机以200Hz的频率记录小球的运动轨迹。由于实验的限制，这三台摄像机的角度可能比较任意，并不是正交的。每个摄像机记录下的都是一幅二维的图像，有其自己的空间坐标系。

图1

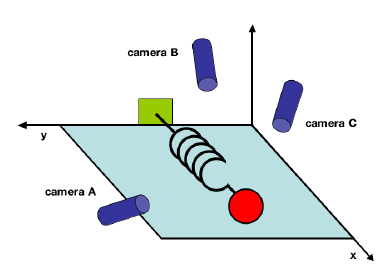
0.2 实验数据表示

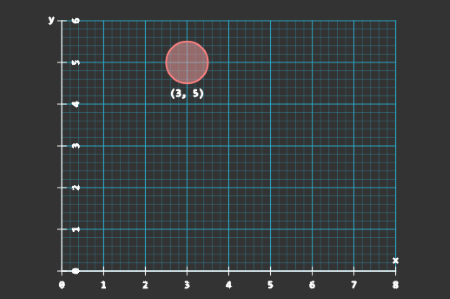
经过几分钟的实验，设置的摄像机记录到了小球的位置序列。每个摄像机在每个时刻记录下的都是一幅二维的图像。对于每张照片，我们可以上看下看左看右看，也可以45°角斜着看。每种不同视角下，照片的坐标轴不同。相应的，我们对图像中点的位置的记录值也不同。如下图，在两种不同的坐标轴下，同一照片上点的位置记录值不同。

在图2中，我们以\(\begin{pmatrix} 1\\0 \end{pmatrix}\)， \(\begin{pmatrix} 0\\1 \end{pmatrix}\)作为基，此时小球的坐标记为\((3, 5)\)

图2

在图3中，我们以向量$\begin{pmatrix} 4/5\\3/5 \end{pmatrix}$， $\begin{pmatrix} -3/5\\4/5 \end{pmatrix}$作为基，此时小球的坐标记为$(5.4, 2.2)$

图3

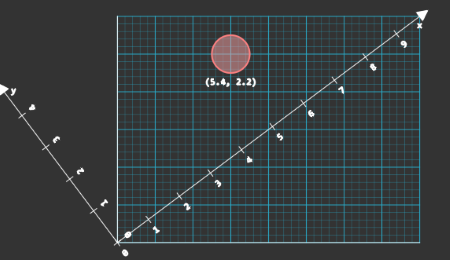
通过上例我们注意到了坐标轴选择与位置记录值之间的关联。

发生在向量与一组数之间的任意一种转化，都被称为一个坐标系。而其中两个特殊的向量——\(\hat{i}\)和\(\hat{j}\)，被称为我们这个标准坐标系的基向量。

习惯上，我们取屏幕坐标作为观测的基准，也就是说，以从左往右的水平轴为x轴，从下至上的垂直轴为y轴。
将实验中摄像机在每个时刻记录到的小球位置作为一个样本，每个样本可以表示为列向量

\[X=\begin{pmatrix} x_A\\y_A\\x_B\\y_B\\x_C\\y_C \end{pmatrix} \]

如果以200Hz的频率拍摄10分钟，将得到10×60×200=120000个这样的向量数据。

从线性代数的角度来描述，摄像机拍摄的照片是一个二维空间，我们选择坐标轴的过程就是选择这个空间的一组基的过程。空间中的任一向量都可以通过基向量的线性组合表示。
一般地，我们会使用标准正交基对空间进行描述。扩展到m维空间，这组基可以表示为行列向量线性无关的单位矩阵：

\[B=\begin{pmatrix} b1\\b2\\...\\b_m \end{pmatrix} = \begin{pmatrix} 1&0&...&0\\0&1&...&0\\\vdots&\vdots&\ddots&\vdots\\0&0&...&1 \end{pmatrix}=I \]

0.3 数据分析

接下来的问题是，如何从这些数据中获取小球的运动规律？

0.3.1 问题分析

实验数据中有这样两类问题影响着我们对小球的真实运动规律的判断：

• 冗余：由于事先不知道小球的运动规律，实验记录的数据中可能存在大量冗余信息，干扰我们的判断
• 噪音：真实实验场景中，空气、摩擦、摄像机误差、非理想化的弹簧等因素都可能使数据变得混乱，掩盖变量间的真实关系

要从实验数据中获取真实运动规律，我们需要排除掉数据中冗余和噪音的干扰。结合上一部分对向量空间、正交基的描述，可以将这个问题理解为：

• 目标：希望从数据中获取小球在x轴上的运动轨迹（在上帝视角中，我们知道小球的位置可以用沿着x轴方向的函数表示，但实际实验过程中并不知道该规律以及真实的x轴在哪）
• 困难：我们观测到的数据因为摄像机设置的位置、其它噪音等因素并不能明显地体现出小球位置和x轴之间的关联
• 解决方法：通过变换观测数据的基向量，我们可以将小球的运动数据转变为以x轴为坐标轴的形式。在这组变换的新数据中，小球位置与x轴的关联容易被发现，在其它维上的位置变化则不明显，因此可以删除其它维上的特征，保留主要特征

从线性代数的角度看，该问题可以描述为：如何寻找到另一组正交基，它们是标准正交基的线性组合，而且能够最好的表示数据集。
PCA就是尝试解决该问题的一种方法。

需要注意的是，这里涉及到了PCA的一个关键假设：线性。
线性假设极大地简化了问题：
（1）线性假设将数据限制在向量空间中，可以被一组基表示
（2）隐含地假设了数据之间的连续性关系
这样一来，数据就可以被表示为各种基的线性组合

现在来尝试回答上面的问题。这个时候，我们会发现问题的定义其实并不明确，到底什么是数据集的最好表示呢？

从对小球运动实验的分析中，我们发现噪音和冗余两个因素会影响我们对实验数据的分析，排除了这些因素的干扰后，对实验数据的分析就变得更加容易了。可以认为，消除了噪音和冗余的数据集表示是一个好的数据集表示。

下面，我们具体定义噪音和冗余。

0.3.2 噪音与冗余

噪音
在信号处理中，噪音的常见衡量方式是信噪比：

\[SNR=\frac{\sigma^2_{signal}}{\sigma^2_{noise}} \]

信噪比认为数据的方差代表不确定性，而不确定性代表信息。假设数据中变化较大的为信号，变化较小的为噪音。信噪比较大时，数据的信息比重较高，信噪比较低则意味着数据中有较多的噪音成分。事实上，这个标准等价于一个低通的滤波器，是一种标准的去噪准则，而变化的大小则是由方差来描述的。

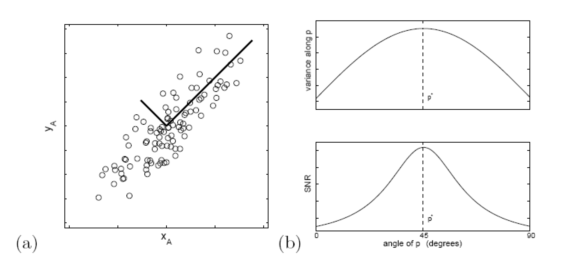
在引例中，假设摄像机A拍摄到的数据如图4(a)所示，圆圈代表采样点，因为运动理论上是只存在于一条直线上的，所以偏离直线的分布都属于噪音。此时信噪比描述的就是在某对垂直方向上概率分布的比值。找出潜在的，最优的x轴事实上等价于寻找空间内的垂直直线，使得信噪比尽可能大。在图中寻找这样的方向，最直接的想法就是对基向量进行旋转。

图4

冗余
在实验中有时会引入不必要的变量。这些变量可能会导致两种情况：

1. 该变量对结果没有影响
2. 该变量可以用其它变量表示，从而造成数据冗余
   

图5

图5中(a)所示的是低冗余的情况，从统计学上说，这两个观测变量是相互独立的，它们之间的信息没有冗余。

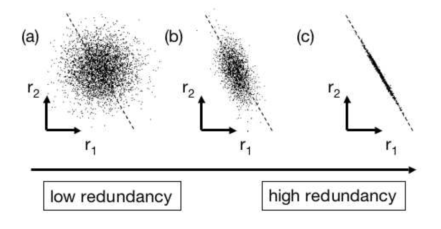
(c)所示的情况是高冗余的，反映了高度相关的记录，在引例中，这可能是因为摄像机A和B的放置位置太近所导致的，也可能是实验设计不合理造成的。在这种情况下，只需要保留一个变量就可以了。

变量间的冗余可以通过协方差进行衡量。
对于观测变量\(A\)，\(B\)，协方差为：

\[\begin{aligned} \sigma_{AB}^2 & = E[(A-E[A])(B-E[B])] \\ &=\frac{\sum_{i=1}^n{(a_i-\bar{a})(b_i-\bar{b})}}{n-1} \end{aligned} \]

将\(A、B\)写成行向量的形式，则协方差可以表示为：

\[\sigma_{AB}^2\equiv\frac{1}{n-1}AB^T \]

根据协方差，可以判断变量间相关性的强弱。如果两个变量的变化趋势一致，则协方差为正值；若趋势相反，则协方差为负值。在两个变量各自方差不变的情况下，协方差绝对值越大，则相关性越强。

在对噪音和冗余进行了定义之后，我们就可以利用线性代数的工具来解决问题了，在下一节中，我们对PCA的求解过程进行介绍。

1 理论分析

1.1 求解目标

记矩阵\(X\)为原始数据集，其中每一列为一个观测样本，\(X\)的大小为\(m\times n\)。
\(X\)的协方差矩阵为

\[C_X\equiv\frac{1}{n-1}XX^T \]

协方差矩阵有以下性质：

• \(C_X\)是一个\(m\times m\)的平方对称矩阵
• \(C_X\)对角线上的元素是对应的观测变量的方差
• 非对角线上的元素是对应的观测变量之间的协方差

\[C_X\equiv\begin{pmatrix}\sigma_{x_1x_1}^2&\sigma_{x_1x_2}^2&...&\sigma_{x_1x_m}^2\\ \sigma_{x_2x_1}^2&\sigma_{x_2x_2}^2&...&\sigma_{x_2x_m}^2\\ \vdots&\vdots&\ddots&\vdots\\ \sigma_{x_mx_1}^2&\sigma_{x_mx_2}^2&...&\sigma_{x_mx_m}^2 \end{pmatrix}\]

协方差矩阵反映了数据的噪音和冗余的程度。对角线上的元素越大，表明信号越强，变量的重要性越高；元素越小则表明可能是存在的噪音或是次要变量。
非对角线的元素大小则对应于相关观测变量对之间冗余程度的大小。

主元分析以及协方差矩阵优化的原则是：

1. 最小化变量冗余：协方差矩阵的非对角元素要尽量小 → 因为协方差矩阵的每项元素均≥0，所以优化目标为非对角元素为0
2. 最大化信号：协方差矩阵的对角线元素尽可能大

1.2 求解过程

记矩阵\(Y\)为另一个大小为\(m×n\)的矩阵，\(Y\)为\(X\)经过线性转换后的矩阵，令转换矩阵\(P\)为正交矩阵：

\[PX=\begin{pmatrix} p_1\\ \vdots \\p_m \end{pmatrix} \begin{pmatrix} x1&...&x_n \end{pmatrix} \]

\[Y=\begin{pmatrix} p_1·x_1&...&p_1·x_n\\ \vdots & \ddots & \vdots\\p_m·x_1&...&p_m·x_n \end{pmatrix} \]

其中，\(p_i\)表示\(P\)的行向量，\(x_i\)表示\(X\)的列向量。另外，记\(y_i\)为\(Y\)的列向量。

\[y_i=\begin{pmatrix} p_1·x_i\\...\\p_m·x_i \end{pmatrix} \]

上式表示不同基之间的转换，其含义如下：

• \(P\)是从\(X\)到\(Y\)的转换矩阵
• \(P\)的行向量，\(\{p_1,p_2,...,p_m\}\)是一组新的基，而\(Y\)是原数据在这组新的基下得到的重新表示

\(y_i\)表示\(x_i\)与\(P\)中对应列的点积，也就相当于在对应向量上的投影。所以，\(P\)的行向量就是一组新的基，它对原数据\(X\)进行重新表示。

这里的计算做了一些约简，所以看起来跟3Blue1Brown教程里基变换的部分不太一致，当我们把\(P\)为正交阵的条件考虑进来，就可以转化为视频中的形式了：
因为\(P\)为正交阵，有\(P^{-1}=P^T\)

\[\begin{aligned} Y &= PX\\ &=\begin{pmatrix} p_1\\ \vdots \\p_m \end{pmatrix} \begin{pmatrix} x1&...&x_n \end{pmatrix}\\ &=\begin{pmatrix}p_1&p_2&...&p_m\end{pmatrix}^{-1}\begin{pmatrix} x1&...&x_n \end{pmatrix} \end{aligned}\]

在线性的假设条件下，问题转化为寻找一组变换后的基，也就是\(P\)的行向量\(\{p_1,p_2,...,p_m\}\)，亦即PCA中的“主元”，使得变换后的矩阵\(Y\)的协方差矩阵为对角阵。通过特征根分解，我们可以实现上述目标，推导如下：

\[\begin{aligned} C_Y & =\frac{1}{n-1}YY^T\\ & = \frac{1}{n-1}(PX)(PX)^T\\ & = \frac{1}{n-1}PXX^TP^T\\ & = \frac{1}{n-1}P(XX^T)P^T \end{aligned} \]

定义\(A=XX^T\)，上式变为：

\[C_Y=\frac{1}{n-1}PAP^T \]

\(A\)为m阶对称矩阵，由对称矩阵性质得，存在正交矩阵\(E\)使得\(E^{-1}AE=E^TAE=\Lambda\)，其中\(\Lambda\)为以\(A\)的r个特征值为对角元的对角矩阵，即\(A=E\Lambda E^T\)。
我们可以取\(P\equiv E^T\)，则\(A=P^T\Lambda P\)
因为\(P\)为正交阵，有\(P^{-1}=P^T\)，因此，\(C_Y\)可化为

\[\begin{aligned} C_Y &=\frac{1}{n-1}PAP^T\\ &= \frac{1}{n-1}P(P^T\Lambda P)P^T\\ &=\frac{1}{n-1}(PP^T)\Lambda(PP^T)\\ &=\frac{1}{n-1}(PP^{-1})\Lambda(PP^{-1})\\ &=\frac{1}{n-1}\Lambda \end{aligned}\]

\(C_Y\)为对角阵，即当\(P\)的行向量为\(XX^T\)的特征向量时，转换后矩阵\(Y\)的协方差矩阵\(C_Y\)为对角阵，\(C_Y\)对角线上的第\(i\)个元素是数据\(X\)再方向\(p_i\)上的方差。

2 PCA求解的一般步骤

1. 对数据集\(X\)所有样本进行中心化
2. 计算样本协方差矩阵\(C_X=\frac{1}{n-1}XX^T\)
3. 对协方差矩阵\(C_X\)进行特征值分解
4. 取最大的\(k\)个特征值对应的特征向量\((p_1^{sorted}, p_2^{sorted}, ..., p_k^{sorted})\)，将所有特征向量标准化后，组成特征向量矩阵\(W\)
5. 对样本集中的每一个样本\(x^{(i)}\)，转化为新的样本\(z^(i)=W^Tx^{(i)}\)
6. 得到输出样本集\(D=(z^{(1)}, z^{(2)}, ..., z^{(k)})\)

3 应用案例-宾夕法尼亚运河系统

在参考资料2中，提供了一个很棒的PCA应用实例。这个例子展示了PCA在问题分析与知识发现上的作用。

（备注：这部分呈现的是SPSS的实验结果，我不太熟悉SPSS的参数和输出，这里结合了参考资料5进行了简单解读。）

3.1 数据介绍

图6

在宾夕法尼亚运河沿线，有多个城市参与到了各类食品的生产运输过程中。现在，我们对运河沿线城市的产品生产情况进行调查，得到数据描述如下。

特征名称	特征描述
town	城市名称
corn_perc	玉米产量比例（占所有城市产量比，下同）
wheat_perc	小麦产量比例
flour_perc	面粉产量比例
whiskey_perc	威士忌产量比例
groceries_perc	食品杂货产量比
dry_goods_perc	干货产量比

比较可惜的是，我没有找到完整的原始数据QAQ，所以我们不能自己对这组数据进行分析练习。下文直接引用了原材料的分析结果。

3.2 结果分析

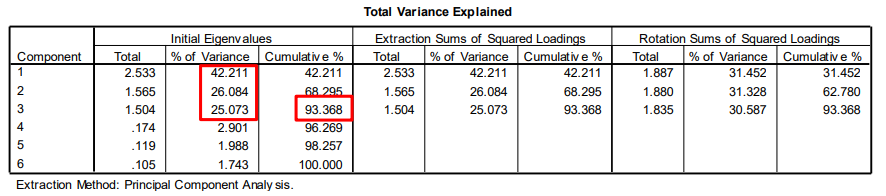
3.2.1 方差贡献率

原始生产数据经过PCA，得到下图所示的结果。左列的数据显示，原始变量中前三个因子的总体方差贡献率达到了93.368%。

图7

3.2.2 因子载荷矩阵

旋转后的因子载荷矩阵如下。

图8

根据上表展示的成分载荷，我们可以对每个主成分进行解释（这也是PCA中最具挑战性的部分）：

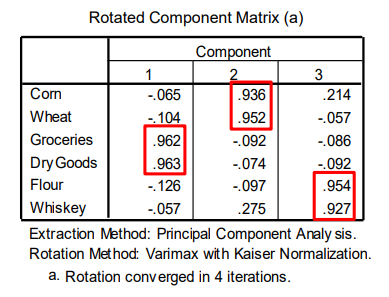
成分id	主要载荷	解释
1	食品杂货、干货	经过较多加工、附加值较高的食品
2	玉米、小麦	食品原材料，无附加值
3	面粉、威士忌	轻度处理、稍有附加值的食品

在解释各个成分的时候，我们根据成分中每个原始特征的载荷来推断成分的含义：

• 成分中载荷越高的特征，对于该成分越重要
• 载荷同时包含正项和负项时，可以解释为“混合的”（mixed）
• 在解释成分时，需要使用旋转成分矩阵（ALWAYS use the ROTATED component matrix!!）

本例中，每个主成分看起来都代表了某种食品加工的程度或附加值的大小。

3.2.3 因子得分

因子得分为我们利用PCA得到的新变量值，下图为本例中所有样本的因子得分：

图9

通过对每个样本（本例中为城市）的因子得分进行分析，可以在我们对因子进行解释时提供帮助。 下图为本例中各成分的样本因子得分分布箱线图，能看到，Easton、Philadelphia和Northmberland是所有城市中比较明显只依赖于某一主成分食品产出的城市。

图10

图11

图12

图13

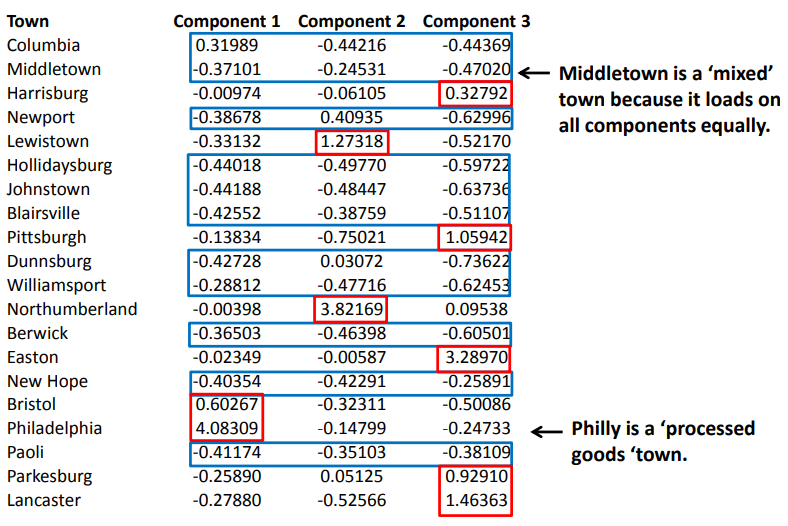
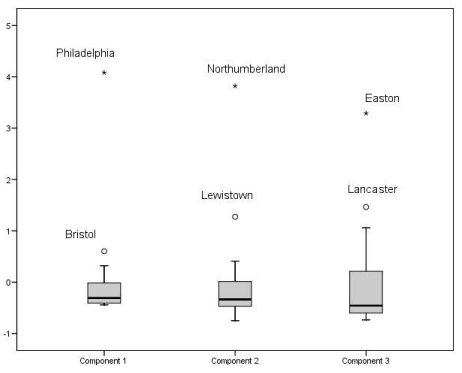
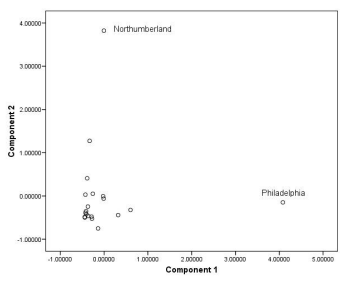
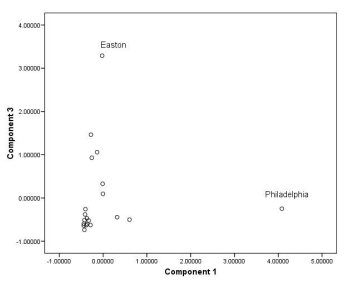
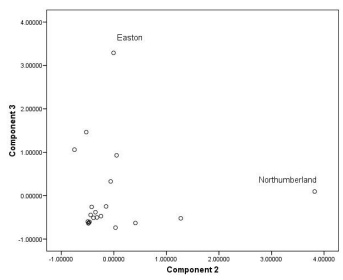
在某个单一因子上得分较高意味着该样本的原始特征很大程度上能够被这个因子所解释。

当我们结合样本地理信息和因子得分及上述步骤中我们得到的对因子的解释，可以发现一些有趣的事实：

图14

图中绿色的点代表因子1载荷较高的样本，红色的点代表因子1载荷较低的样本。 可以看到因子1所代表的对食品加工程度较高的城市基本位于宾夕法尼亚运河东段。这些城市也基本属于在哥伦比亚铁路沿线的工业城市。

图15

因子2对应的分布图则表明，食品原材料产出较多的城市主要分布在运河中段。这些城市大多属于小的农业城市。

图16

因子3对应分布图展现了以食品半成品为主要产出的城市分布。这部分城市大多为中型城市。

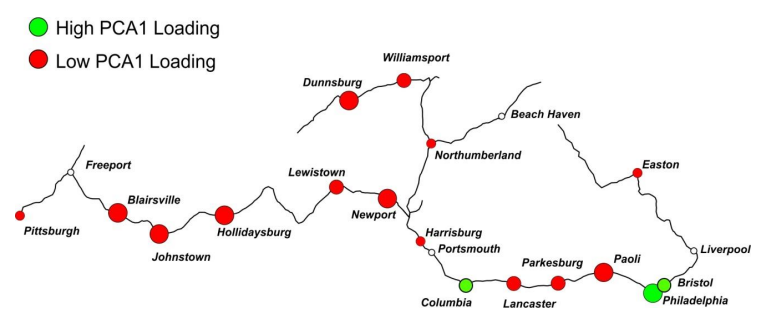
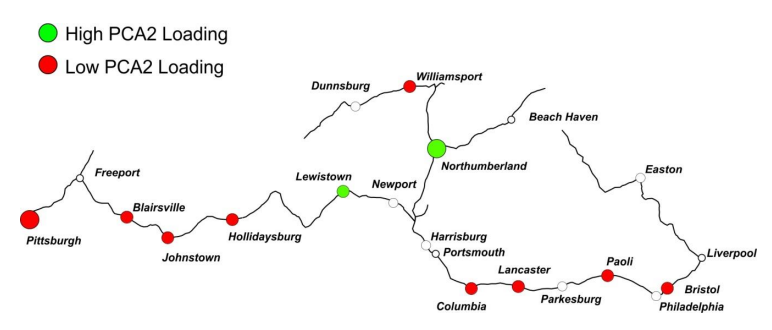
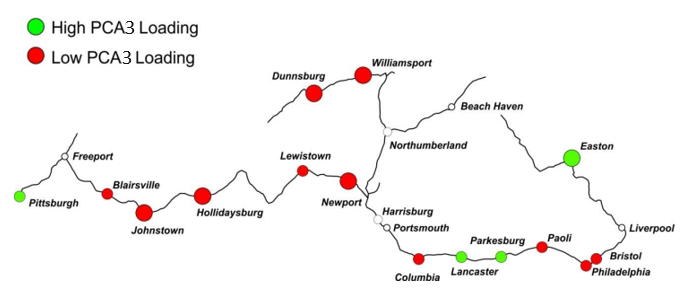
不通过PCA，这些关联可能并没有那么显而易见。

4 优缺点总结

4.1 优点

• PCA能够对数据进行降维处理，通过对求出的“主元”向量重要性排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维从而简化模型或是对数据进行压缩的效果，同时最大程度的保持了原有数据的信息。
• PCA无参数限制，在计算过程中不需要人为设定参数或根据任何经验模型对计算进行干预，最后的结果只与数据相关，与用户是独立的。

4.2 缺点

• 在用户对观测对象具有一定先验知识时，无法通过参数化等方法对PCA处理过程进行干预，可能达不到预期的效果，效率不高。
• 当数据不满足高斯分布时，PCA方法得出的主元可能不是最优的。
• 主成分各个维度的含义具有一定模糊性，不如原始样本特征的解释性强。

5 参考资料

[1] Shlens J. A tutorial on principal component analysis[J]. arXiv preprint arXiv:1404.1100, 2014.
[2] https://www3.cs.stonybrook.edu/~mueller/teaching/cse564/Lec 17 - Principal Component Analysis.pdf
[3] 3Blue1Brown(10.18,2016). 线性代数的本质-系列合集
[4] 刘建平Pinard(12.31,2016). 主成分分析（PCA）原理总结
[5] 莫子非(6.30,2021). 因子分析有啥用？怎么使用SPSS做因子分析？