[因果推断工具箱] 混杂与去混杂
一、引子
在介绍混杂的定义及处理方法前,让我们通过一个例子直观地理解混杂。
1998年,《新英格兰医学杂志》的一项研究显示,退休男子经常散步和其死亡率下降之间存在关联。研究的具体情况如下:
研究问题:勤于运动的人是否更长寿
研究方法:追踪707人作为调查样本,在12年追踪期内记录其步行活动习惯和死亡率
观察结果:每天散步不到1英里的男性(“偶尔步行者”)的死亡率比每天步行超过2英里的男性(“经常步行者”)高出2倍
该研究可能存在的问题是,研究者没有规定谁来做偶尔步行者,谁来做经常步行者。调查样本中年轻的男性可能更愿意进行积极的锻炼,那么其在追踪期内的死亡率自然相对较低。此时,年龄因素可能影响我们对步行和死亡率之间因果关系的判断。我们称该问题中的年龄为混杂因子。
可以用因果图对问题进行描述:
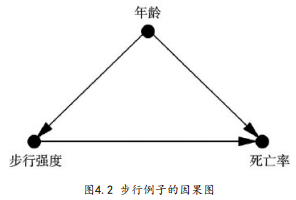
该研究中的其它因素也可能为混杂因子,如身体条件、饮食习惯等。
二、混杂
在研究中,记试验中的处理为X,结果为Y。我们想回答的问题是,X与Y之间的因果关系是怎样的。该因果关系可以通过干预概率\(P(Y|do(X))\)获得,而我们在试验中所能观察到的仅为给定处理条件的条件概率\(P(Y|X)\)。混杂的存在使得我们无法通过试验直接判断X、Y之间的因果关系。
混杂:任何使得给定处理效应的条件概率\(P(Y|X)≠P(Y|do(X))\)的因素。
混杂偏倚(confounding bias):当一个变量同时影响到选择接受处理的对象以及试验结果时产生。
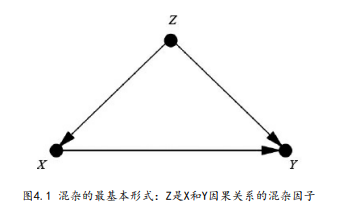
例如:假设我们准备测试一种药物,而在试验过程中,我们让比对照组平均年龄更低的一组患者服用了这种药物,那么年龄就成为这一试验的一个混杂因子。如果我们没有关于年龄的数据,我们将无法从药物的虚假效果中区分出药物的真实效果。
三、去混杂方法
3.1 Z调整/Z控制
在引例中,如果确定了混杂因子Z为年龄,可以分别比较每个年龄组的处理组和对照组。然后,根据各个年龄组在目标总体中所占的百分比对每个年龄组进行加权,就可以计算出药物的平均效果。
3.2 随机对照试验(randomized controlled trial, RCT)
在随机对照试验中,处理X被随机地分配给某些个体,而不分配给其它个体,之后我们需要对比在两组个体中观察到的结果变量Y的变化的差异。例如,在引例中随机安排受试者的步行情况。
优点:
- 消除了混杂偏倚
- 使研究者能够量化不确定性
缺点:
- 干预可能在事实上不可行或不道德
例如:研究肥胖对心脏病的影响时,无法随机安排病人肥胖与否;研究吸烟的影响时,不能要求随机抽取的人抽10年的烟 - 受试者可能无法代表目标总体
对于某些较为复杂、参与起来不方便的试验,可能在招募受试者时遇到困难,而勉强找到的志愿参与者又无法代表我们的目标总体
3.3 后门标准(back-door criterion)
后门标准可以明确识别出因果图中哪些变量是去混因子,如果研究者能够收集到这些变量的数据,那么就可以对这些变量进行统计调整,从而在不真正实施干预的情况下对干预的结果做出预测。
do算子:do算子会清除指向X的所有箭头,这样可以防止有关X的任何信息在非因果方向流动。随机化处理具有同样的效果。若选择合适的变量进行统计调整,也具有同样的效果。
后门路径(back-door path):所有X和Y之间以指向X的箭头为开始的路径,这些路径允许X和Y之间的伪相关信息在管道中流通。
阻断因果图中所有的后门路径,则完成了对X和Y的去混杂。若我们试图通过某一组变量Z来实现这一点,则还需要确保Z的任何成员都不是X的后代,否则我们就可能部分或完全地关闭这条X与Y之间的因果路径。
关于如何阻断因果图中信息的流通,参见我的上一篇博客[因果推断工具箱] 因果图
下面为几个利用后门路径去混杂的例子:
1.
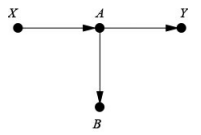
在图中,不存在指向X的后门路径,不需要进行去混杂。
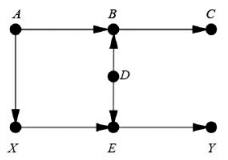
在该图中,存在一个后门路径X←A→B←D→E→Y。该路径已经被对撞接合A→B←D阻断了,所以不需要对任何因素进行控制。
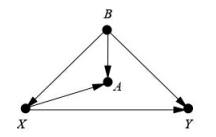
在该图中,存在后门路径X←B→Y,需要控制B来阻断该路径,如果B无法被观测到,那么不进行随机对照试验就无法估计X对Y的因果效应。
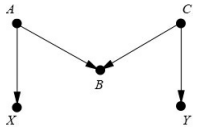
该图中有后门路径X←A→B←C→Y,该路径被B处的对撞所阻断,不需要控制任何事物。这种偏倚形式被称为“M偏倚”。
该偏倚的一个实例为:
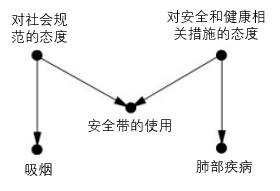
在实际数据中,人们发现安全带的使用与吸烟和肺部疾病均相关。
若单独控制安全带的使用情况,则无法估计吸烟对肺部疾病的因果效应。
若同时控制对社会规范的态度、安全带的使用、对安全和健康相关措施的态度,那么该后门路径会再次被阻断,可以观察吸烟与肺部疾病的因果效应。
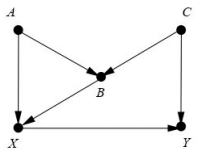
图中存在两个后门路径X←B←C→Y和X←A→B←C→Y。其中,第二条为M型路径,无需控制。我们需要关闭第一条路径。
若控制B,则打开了M型路径,需要再控制A和C以关闭M型路径。
若控制C,则关闭第一条路径而不影响其它路径。
参考资料
朱迪亚·珀尔,达纳·麦肯齐 著,江生,于华 译,“为什么:关于因果关系的新科学”,中信出版集团,2019.

![[因果推断工具箱] 混杂与去混杂](https://img2022.cnblogs.com/blog/2322623/202205/2322623-20220513131603934-263045320.png) 本文为Judea Pearl《The Book of Why》的读书笔记,整理了书中对第四章对混杂及去混杂的介绍。
本文为Judea Pearl《The Book of Why》的读书笔记,整理了书中对第四章对混杂及去混杂的介绍。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号