排序（二）交换排序：冒泡排序与快速排序

冒泡排序

　　冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。 

　　算法描述

• 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
• 针对所有的元素重复以上的步骤，除了最后一个；
• 重复步骤1~3，直到排序完成。

　　动图演示

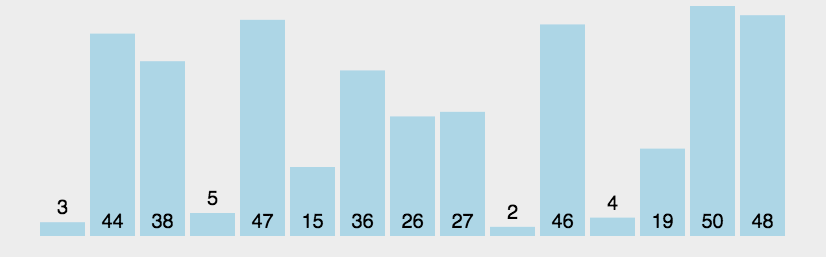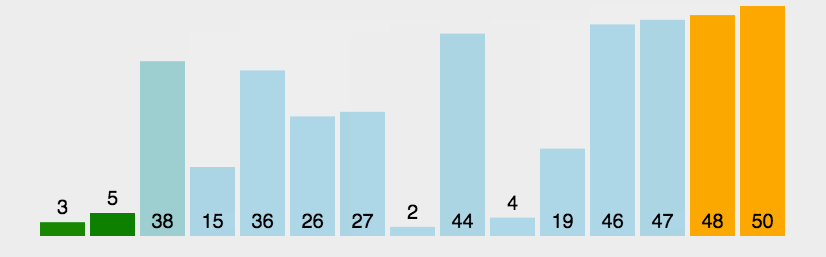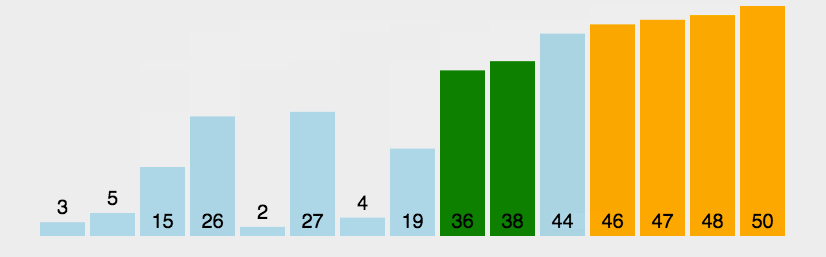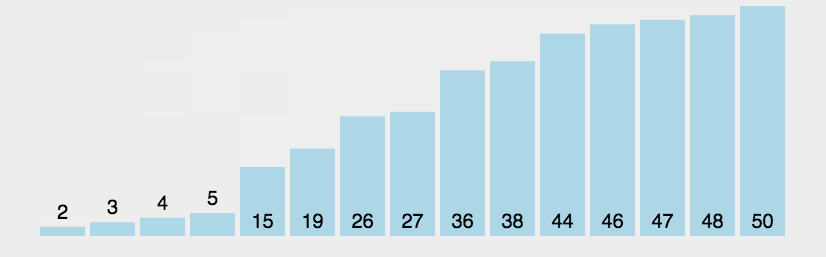
 　　实例验证

　　10000个数字组成的数组排序，耗时大概率在460ms-480ms。

public class TestBubbleSort {

    public static void main(String[] args) {
        System.out.println("old:" + Arrays.asList(Data.array).toString().substring(0, 100) + "...");
        Long start = System.currentTimeMillis();
        sort(Data.array);
        Long end = System.currentTimeMillis();
        System.out.println("new:" + Arrays.asList(Data.array).toString().substring(0, 100) + "...");
        System.out.println("耗时:" + (end - start));
    }

    /**
     * 1.比较相邻的元素。如果第一个比第二个大，就交换它们两个；<br>
     * 2.对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数； <br>
     * 3.针对所有的元素重复以上的步骤，除了最后一个；<br>
     * 4.重复步骤1~3，直到排序完成。<br>
     */
    static void sort(Integer[] array) {
        // 外层循环控制比较次数
        for (Integer i = 0; i < array.length - 1; i++) {
            // 内层循环控制到达位置
            for (Integer j = 0; j < array.length - 1 - i; j++) {
                if (array[j] > array[j + 1]) {
                    Integer data = array[j];
                    array[j] = array[j + 1];
                    array[j + 1] = data;
                }
            }
        }
    }
}

class Data {
    public static Integer[] array;
    static {
        array = new Integer[10000];
        for (Integer i = 0; i < 10000; i++) {
            Random r = new Random();
            array[i] = r.nextInt(100000);
        }
    }
}

　　结果展示：

old:[49773, 80876, 42906, 19675, 75742, 87701, 14611, 18207, 58390, 1921, 45655, 80129, 3414, 71415, 874...
new:[11, 37, 44, 62, 63, 68, 73, 95, 99, 103, 111, 120, 129, 138, 143, 160, 179, 180, 196, 205, 206, 209...
耗时:464

 　　复杂度分析

平均时间复杂度	最好情况	最坏情况	空间复杂度
O(n²)	O(n)	O(n²)	O(1)

　　冒泡排序是最容易实现的排序, 最坏的情况是每次都需要交换, 共需遍历并交换将近n²/2次, 时间复杂度为O(n²). 最佳的情况是内循环遍历一次后发现排序是对的, 因此退出循环, 时间复杂度为O(n). 平均来讲, 时间复杂度为O(n²). 由于冒泡排序中只有缓存的temp变量需要内存空间, 因此空间复杂度为常量O(1).

 

快速排序

　　快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

　　算法描述

• 从数列中挑出一个元素，称为 “基准”(pivot) 默认为第一个数；
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

　　动图演示

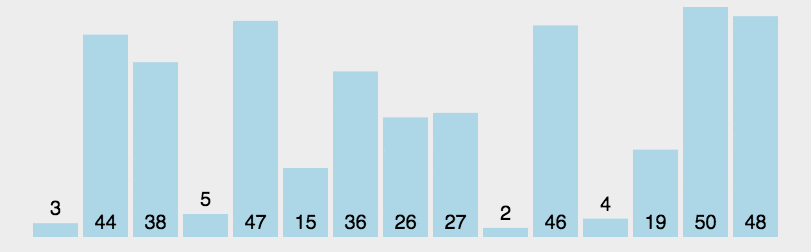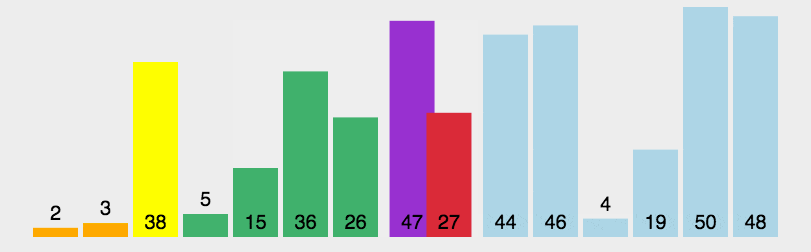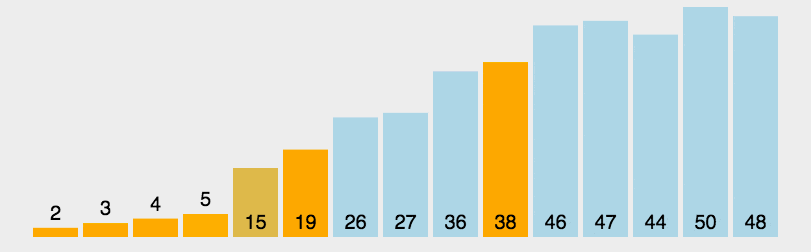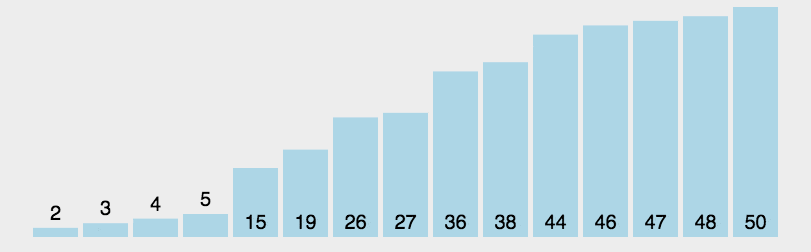
　　实例验证

　　10000个数字组成的数组排序，耗时在10ms以内。

public class TestQuickSort {
    public static void main(String[] args) {
        System.out.println("old:" + Arrays.asList(QuickData.array).toString() + "...");
        Long start = System.currentTimeMillis();
        sort(QuickData.array, 0, QuickData.array.length - 1, "全排");
        Long end = System.currentTimeMillis();
        System.out.println("new:" + Arrays.asList(QuickData.array).toString() + "...");
        System.out.println("耗时:" + (end - start));
    }

    /**
     * 1.先从数列中取出一个数作为key值； <br>
     * 2.将比这个数小的数全部放在它的左边，大于或等于它的数全部放在它的右边； <br>
     * 3.对左右两个小数列重复第二步，直至各区间只有1个数。
     */
    static void sort(Integer[] array, int low, int high, String desc) {
        if (low < high) {
            int i = getMiddle(array, low, high, desc);
            sort(array, low, i - 1, "左排");
            sort(array, i + 1, high, "右排");
        }
    }

    private static int getMiddle(Integer[] array, int low, int high, String desc) {
        System.out.println("----------------------");
        System.out.println(desc + "-getMiddle before:" + Arrays.asList(QuickData.array).toString() + "...");
        int left = low;
        int right = high;
        // 保存基准的值
        int pivot = array[low];
        while (left < right) {
            // 从后向前找到比基准小的元素位置right
            while (array[right] >= pivot && left < right)
                right--;
            // 从前往后找到比基准大的元素位置left
            while (array[left] <= pivot && left < right)
                left++;
            // 此时array[left]>pivot>array[right]，交换left与right元素的位置
            if (left < right) {
                int temp = array[left];
                array[left] = array[right];
                array[right] = temp;
            }

        }
        // 交换基准元素与中界元素的值
        array[low] = array[left];
        array[left] = pivot;
        System.out.println(desc + "-getMiddle end:" + Arrays.asList(QuickData.array).toString() + "...");
        System.out.println(desc + "-middle:" + array[left] + " index:" + left);
        return left;
    }
}

class QuickData {
    public static Integer[] array;
    static {
        array = new Integer[10];
        for (Integer i = 0; i < 10; i++) {
            Random r = new Random();
            array[i] = r.nextInt(100);
        }
    }
}

　　结果展示：

old:[84, 74, 45, 26, 23, 9, 91, 50, 12, 14]...
----------------------
全排-getMiddle before:[84, 74, 45, 26, 23, 9, 91, 50, 12, 14]...
全排-getMiddle end:[12, 74, 45, 26, 23, 9, 14, 50, 84, 91]...
全排-middle:84 index:8
----------------------
左排-getMiddle before:[12, 74, 45, 26, 23, 9, 14, 50, 84, 91]...
左排-getMiddle end:[9, 12, 45, 26, 23, 74, 14, 50, 84, 91]...
左排-middle:12 index:1
----------------------
右排-getMiddle before:[9, 12, 45, 26, 23, 74, 14, 50, 84, 91]...
右排-getMiddle end:[9, 12, 14, 26, 23, 45, 74, 50, 84, 91]...
右排-middle:45 index:5
----------------------
左排-getMiddle before:[9, 12, 14, 26, 23, 45, 74, 50, 84, 91]...
左排-getMiddle end:[9, 12, 14, 26, 23, 45, 74, 50, 84, 91]...
左排-middle:14 index:2
----------------------
右排-getMiddle before:[9, 12, 14, 26, 23, 45, 74, 50, 84, 91]...
右排-getMiddle end:[9, 12, 14, 23, 26, 45, 74, 50, 84, 91]...
右排-middle:26 index:4
----------------------
右排-getMiddle before:[9, 12, 14, 23, 26, 45, 74, 50, 84, 91]...
右排-getMiddle end:[9, 12, 14, 23, 26, 45, 50, 74, 84, 91]...
右排-middle:74 index:7
new:[9, 12, 14, 23, 26, 45, 50, 74, 84, 91]...
耗时:1

　　复杂度分析

平均时间复杂度	最好情况	最坏情况	空间复杂度
O(nlog₂n)	O(nlog₂n)	O(n²)	O(1)