排序（一）简介
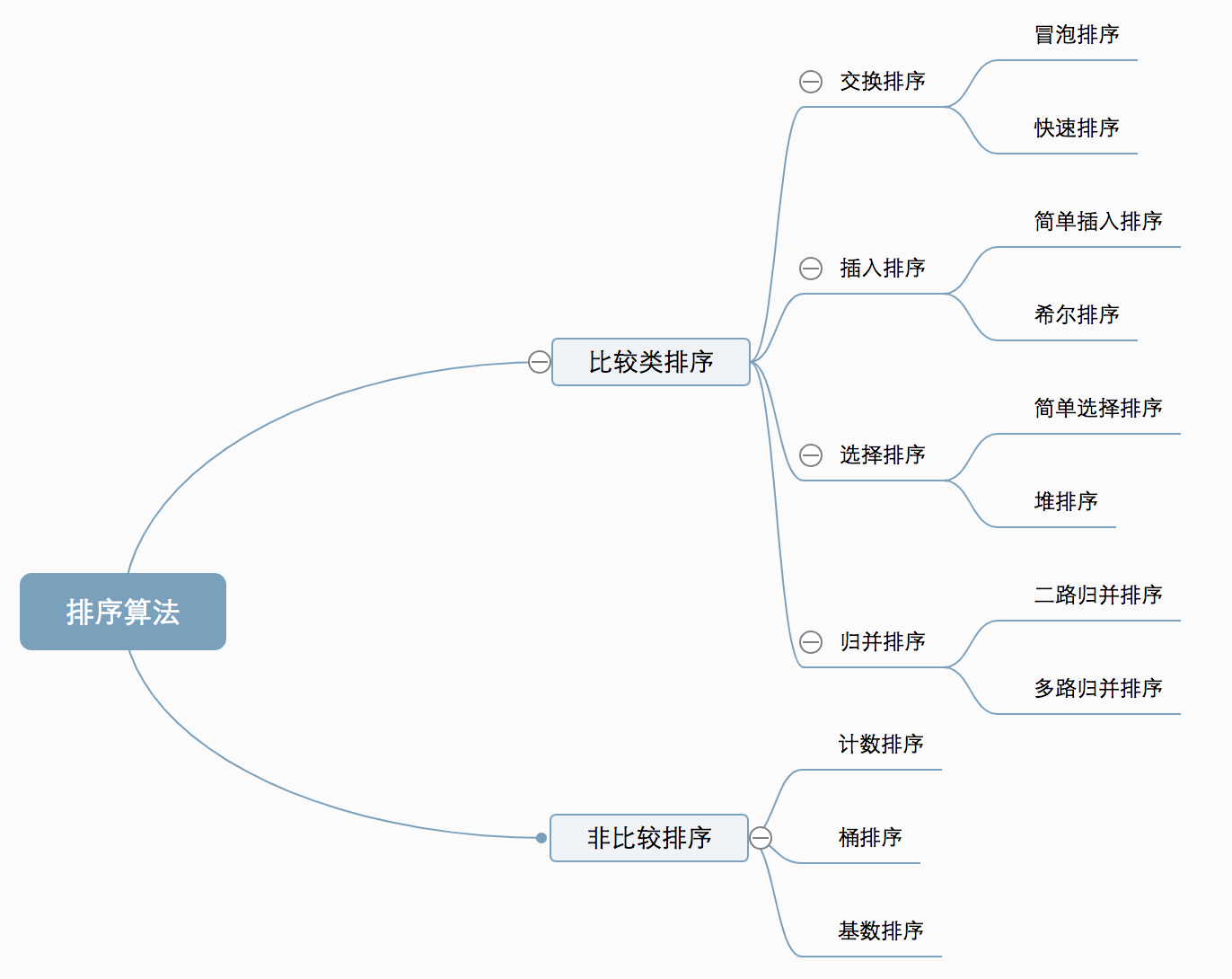
算法分类
- 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。
- 非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。
算法比较
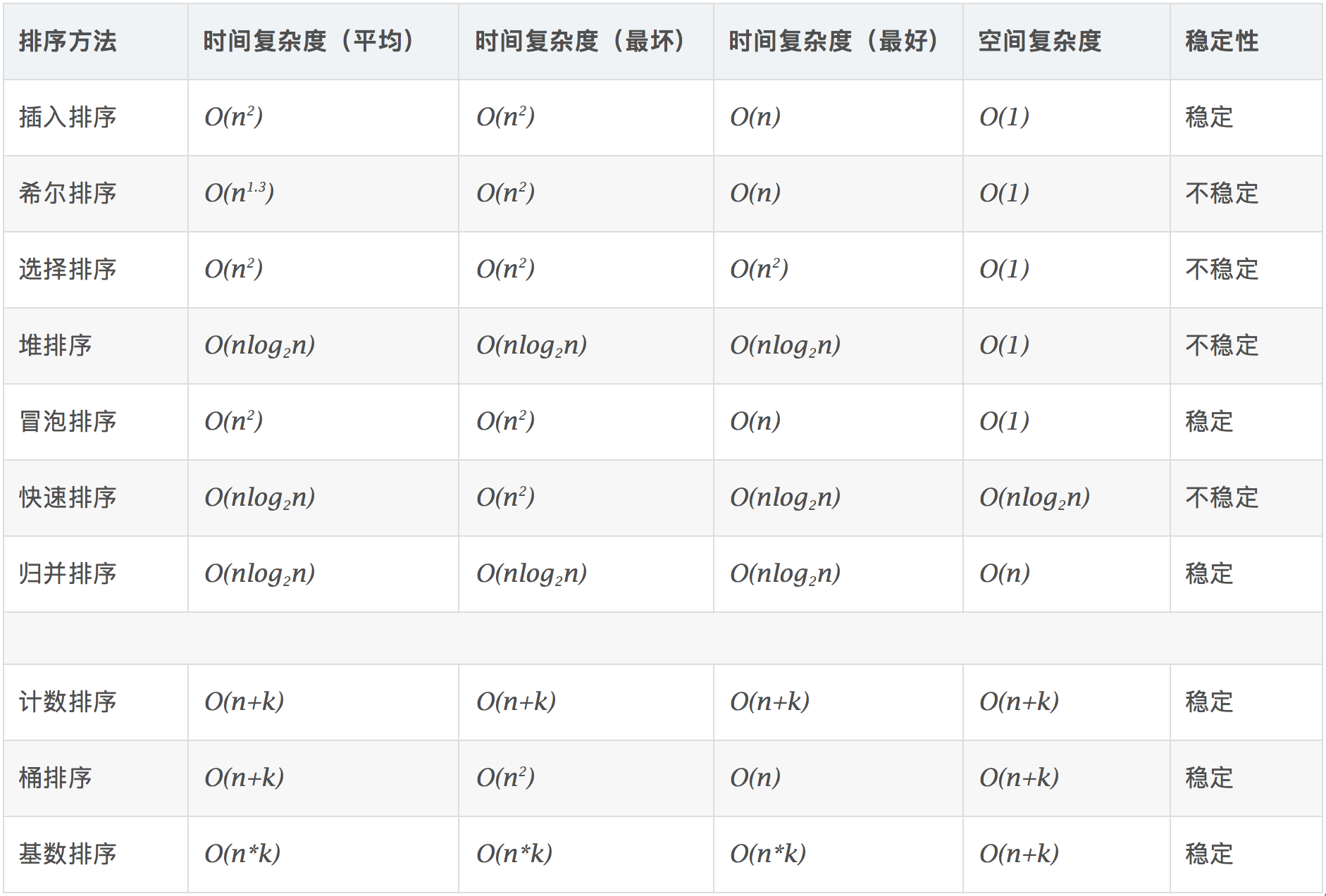
时间复杂度：
1.时间复杂度可以认为是对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。 2.常见的时间复杂度有：常数阶O(1),对数阶O(log2n),线性阶O(n), 线性对数阶O(nlog2n),平方阶O(n2)。 3.时间复杂度O(1)：算法中语句执行次数为一个常数，则时间复杂度为O(1)。
空间复杂度：
1.空间复杂度是指算法在计算机内执行时所需存储空间的度量，它也是问题规模n的函数。 2.空间复杂度O(1)：当一个算法的空间复杂度为一个常量，即不随被处理数据量n的大小而改变时，可表示为O(1)。 3.空间复杂度O(log2N)：当一个算法的空间复杂度与以2为底的n的对数成正比时，可表示为O(log2n) ， ax=N，则x=logaN。 4.空间复杂度O(n)：当一个算法的空间复杂度与n成线性比例关系时，可表示为0(n)。
排序算法稳定性：
稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。 不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。
