算法笔记-二叉树
之前说的栈和队列都是线性表结构,树是非线性表结构。
关于树的常用概念:根节点、叶子节点、父节点、子节点、兄弟节点,还有节点的高度、深度、层数,以及树的高度。

最常用的树就是二叉树(Binary Tree)。二叉树的每个节点最多有两个子节点,分别是左子节点和右子节点。
二叉树中,有两种比较特殊的树,分别是满二叉树和完全二叉树。满二叉树又是完全二叉树的一种特殊情况。
二叉树的两种存储方式:
- 用链式存储:
-
- 每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节点的指针。
- 我们只要拎住根节点,就可以通过左右子节点的指针,把整棵树都串起来。
- 这种存储方式我们比较常用。大部分二叉树代码都是通过这种结构来实现的。
![]()
- 用数组顺序存储:
-
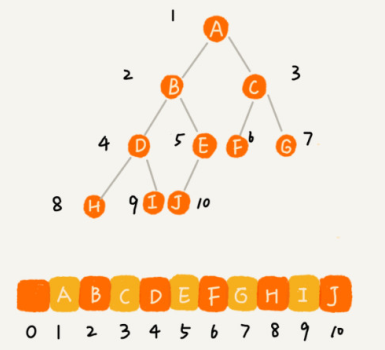
- 如果节点 X 存储在数组中下标为 i 的位置,下标为 2 * i 的位置存储的就是左子节点,下标为 2 * i + 1 的位置存储的就是右子节点。
- 反过来,下标为 i/2 的位置存储就是它的父节点。
- 通过这种方式,我们只要知道根节点存储的位置(一般情况下,为了方便计算子节点,根节点会存储在下标为 1 的位置),这样就可以通过下标计算,把整棵树都串起来。
- 数组顺序存储的方式比较适合 完全二叉树,其他类型的二叉树用数组存储会比较浪费存储空间。
![]()
如果某棵二叉树是一棵完全二叉树,那用数组存储是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样,要存储额外的左右子节点的指针。(这也是为什么完全二叉树会单独拎出来的原因,也是为什么完全二叉树要求最后一层的子节点都靠左的原因。)堆 就是一种完全二叉树,最常用的存储方式就是数组。
【二叉树的遍历】
二叉树里非常重要的操作就是前序遍历、中序遍历、后序遍历,用递归代码来实现遍历的时间复杂度是 O(n)。其中,前、中、后序,表示的是节点与它的左右子树节点遍历打印的先后顺序。
- 前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
-
- preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
- 中序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
-
- inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
- 后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
-
- postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r
【二叉查找树(Binary Search Tree)】
二叉查找树是为了实现快速查找而生的,它不仅仅支持快速查找一个数据,还支持快速插入、删除一个数据。
二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。
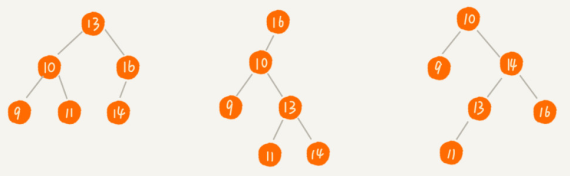
1. 二叉查找树的查找操作
先取根节点,如果它等于我们要查找的数据,那就返回。如果要查找的数据比根节点的值小,那就在左子树中递归查找;如果要查找的数据比根节点的值大,那就在右子树中递归查找。(感觉有点像 二分查找)
2. 二叉查找树的插入操作
二叉查找树的插入过程有点类似查找操作。新插入的数据一般都是在叶子节点上,所以我们只需要从根节点开始,依次比较要插入的数据和节点的大小关系。如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新数据直接插到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。同理,如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
3. 二叉查找树的删除操作
针对要删除节点的子节点个数的不同,需要分三种情况来处理:
- 如果要删除的节点没有子节点,我们只需要直接将父节点中,指向要删除节点的指针置为 null。
- 如果要删除的节点只有一个子节点(只有左子节点或者右子节点),我们只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就可以了。
- 如果要删除的节点有两个子节点,需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,我们可以应用上面两条规则来删除这个最小节点。
4. 二叉查找树的其他操作
二叉查找树中还可以支持快速地查找最大节点和最小节点、前驱节点和后继节点。
二叉查找树还有一个重要的特性,就是中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是 O(n),非常高效。因此,二叉查找树也叫作二叉排序树。
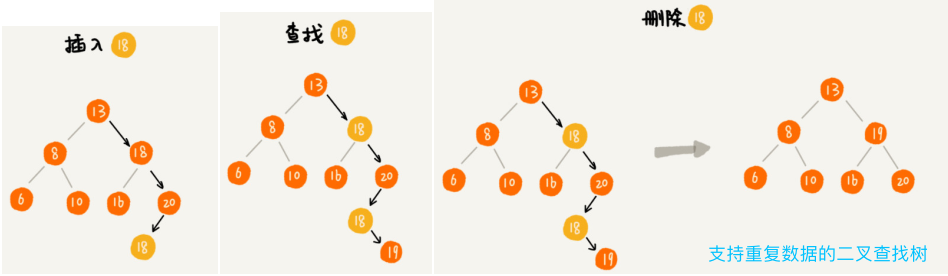
支持重复数据的二叉查找树:如果存储的两个对象键值相同,有两种解决方法。
- 第一种方法:二叉查找树中每一个节点不仅会存储一个数据,因此我们通过链表和支持动态扩容的数组等数据结构,把值相同的数据都存储在同一个节点上。
- 第二种方法:每个节点仍然只存储一个数据。在查找插入位置的过程中,如果碰到一个节点的值,与要插入数据的值相同,我们就将这个要插入的数据放到这个节点的右子树,也就是说,把这个新插入的数据当作大于这个节点的值来处理。当要查找数据的时候,遇到值相同的节点,我们并不停止查找操作,而是继续在右子树中查找,直到遇到叶子节点,才停止。这样就可以把键值等于要查找值的所有节点都找出来。对于删除操作,我们也需要先查找到每个要删除的节点,然后再按前面讲的删除操作的方法,依次删除。
二叉查找树的时间复杂度分析:
完全二叉树(或满二叉树),不管操作是插入、删除还是查找,时间复杂度其实都跟树的高度成正比,也就是 O(height)。二叉查找树在比较平衡的情况下,插入、删除、查找操作时间复杂度是O(logn)。
* 有了高效的散列表(时间复杂度是 O(1)),为什么还需要二叉查找树?
- 散列表中的数据是无序存储的,如果要输出有序的数据,需要先进行排序。而对于二叉查找树来说,我们只需要中序遍历,就可以在 O(n) 的时间复杂度内,输出有序的数据序列。
- 散列表扩容耗时很多,而且当遇到散列冲突时,性能不稳定,尽管二叉查找树的性能不稳定,但是在工程中,我们最常用的平衡二叉查找树的性能非常稳定,时间复杂度稳定在O(logn)。
- 笼统地来说,尽管散列表的查找等操作的时间复杂度是常量级的,但因为哈希冲突的存在,这个常量不一定比 logn 小,所以实际的查找速度可能不一定比 O(logn) 快。加上哈希函数的耗时,也不一定就比平衡二叉查找树的效率高。
- 散列表的构造比二叉查找树要复杂,需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题,而且这个问题的解决方案比较成熟、固定。
- 为了避免过多的散列冲突,散列表装载因子不能太大,特别是基于开放寻址法解决冲突的散列表,不然会浪费一定的存储空间。
综合这几点,平衡二叉查找树在某些方面还是优于散列表的,所以,这两者的存在并不冲突。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号