20145333 《信息安全系统设计基础》第三周学习总结

20145333 《信息安全系统设计基础》第三周学习总结

教材学习内容总结

第2章 信息的表示和处理

• 三种数字表示

无符号编码基于传统的二进制表示法，表示大于或者等于零的数字。

补码编码是表示有符号整数的最常见的方式，有符号整数就是可以为正或者为负的数字。

浮点数编码是表示实数的科学计数法的以二为基数的版本。

计算机的表示法是用有限数量的位来对一个数字编码，因此，当结果太大以至不能表示时，某些运算就会溢出，导致计算结果错误。

• 信息存储

大多数计算机使用8位的块来作为最小的可寻址的存储器单位，而不是访问访问存储器中单独的位。存储器的每个字节都由一个唯一的数字来标识，称为它的地址，所有可能地址的集合就称为虚拟地址空间。编译器和运行是系统的一个任务就是将这个存储器空间划分为更可管理的单元，来存放不同的程序对象，也就是程序数据、指令和控制信息，然后有各种机制可以用来分配和管理程序不同部分的存储，这种管理其实完全是在虚拟地址空间里完成的。

• 十六进制表示法

由于十进制和二进制表示法对于描述为模式来说都不是非常方便，所以引进了另一种替代的方法，也就是十六进制数来书写位模式。表示方法：以0x或0X开头，数字“0”～“9”和字符“A”～“F”来表示16个可能的值。取值范围：0016～FF16。

二进制和十六进制之间的转换是简单直接的，可以通过展开每个十六进制数字，将它转换位二进制格式，反过来如果给定一个二进制数字，则可以通过首先将它分割为每四位一组来把它转换为十六进制，当位总数不是四的倍数，最左边的一组可以少于四位，前面用零补足。

当值x是2的幂时也就是对于某个n，x=2∧n，可以很容易地将x写成十六进制形式，只要知道x的二进制表示就是1后面跟n个零。十六进制数字0代表四个二进制0.所以对于被写成i+4j形式的n来说，其中0≤i≥3，可以把x写成开头的十六进制数字为1（i=0）、2（i=1）、4（i=2）或者8（i=3），然后跟着j个十六进制的0。比如，x=2048=211，有n=11=3+4*2，从而得到十六进制表示0x800。

十六进制数之间的加减法：将执行十进制加减法所使用的方法改成以16位基数。

• 字

每台计算机都有一个字长，指明整数和指针数据的标称大小，字长决定虚拟地址空间的最大大小。

• 寻址和字节顺序

多字节对象被存储为连续的字节序列，对象的地址为所使用字节中最小的地址。

存储器中按照从最低有效字节到最高有效字节的顺序存储对象的方式称为小端法。按照从最高有效字节到最低有效字节的顺序存储对象的方式称为大端法。

书写字节序列的子让方式是最低位字节在左边，最高位字节在右边。

• 布尔代数简介

所有逻辑运算都可以用与、或、非表达（最大式、最小式），而与或非可以用“与非”或“或非”表达，所以，只要一个与非门，就可以完成所有的逻辑运算。

掩码是位运算的重要应用，对特定位可以置一，可以清零。

• 整数表示

无符号数的编码：假设一个整数数据类型有w位。我们可以将位向量写成x→，表示整个向量，或者写成[xw-1 ，xw-2，…，x0]，表示向量中的每一位。把x→看做一个二进制表示的数，就获得了x→的无符号表示。

无符号二进制有一个很重要的属性，就是每个介于0~2^w-1之间的整数都有唯一一个w为的值编码，函数为一个双射。

补码编码最常见的有符号数的计算机表示方式就是补码形式。在这个定义中，将字的最高有效位解释为负权。所能表示的数值范围[-2^(w-1)~2(w-1)-1]，在可表示的范围内每个数字 都有一个唯一的w位的补码编码，函数为一个双射。

注意：（1）补码的利用寄存器的长度是固定的特性简化数学运算。（2）补码的范围是不对称的。（3）最大的无符号数值刚好比补码的最大值的两倍大一点：UMaxw = 2 TMaxw + 1。补码表示中所有表示负数的位模式在无符号表示中都变成了正数。

反码除了最高有效位的权是-(2w-1-1)而不是-2w-1，它和补码是一样的。

原码最高有效位是符号位用来确定剩下的位应该取负权还是正权。

C语言允许有符号数与无符号数之间的转换，转换的原则是底层的位表示保持不变。

零扩展将一个无符号数转换为一个更大的数据类型，只需要简单地在表示的开头添加0。

符号扩展将一个补码数字转换为一个更大的数据类型，规则是在表示中添加最高有效位的值的副本。由此可知，如果原始值的位表示为[xw-1，xw-2，…，x0]，那么扩展后的表示就为[xw-1，…，xw-1，xw-1，xw-2，…，x0]。

截断数字将一个w位的数x=[xw-1 ，xw-2，…，x0]截断为一个k位的数字时，会丢弃高w-k位，得到一个位向量[xk-1 ，xk-2，…，x0]，截断一个数字可能会改变他的值——溢出的一种形式。

有符号数到无符号数的隐式强制类型转换导致了某些非直观的行为。而这些非直观的特性经常导致程序错误，并且这种包含隐式强制类型转换细微差别的错误很难被发现。因为这种强制类型转换是在代码中没有明确指示的情况下发生的，程序员经常忽视了它的影响。

• 浮点数

1.IEEE浮点标准用V = (-1)^s × M × 2^E的形式来表示一个数：

符号s决定这个数是负数（s=1）还是正数（s=0），而对于数值0的符号位解释作为特殊情况处理。

尾数M是一个二进制小数，它的范围是1～2-ε，或者是0～1-ε。

阶码E的作用是对浮点数加权，这个权重是2的E次幂（可能是负数）。

2.将浮点数的位表示划分为三个字段，分别对这些值进行编码：

一个单独的符号位s直接编码符号s。

k位的阶码字段exp = ek-1…e1e0编码阶码E。

n位小数字段frac = fn-1…f1 f0编码尾数M，但是编码出来的值也依赖于阶码字段的值是否等于0。

练习

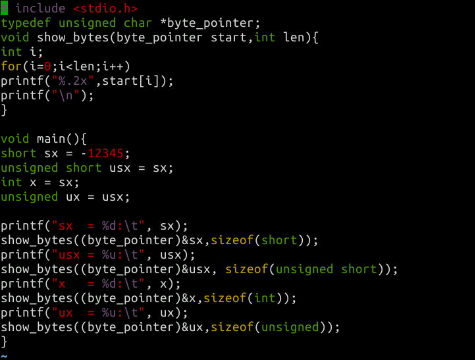
• p28 参考p30代码，写个main函数测试show_bytes

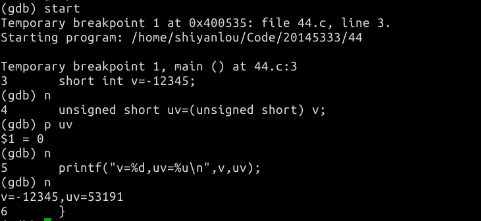
• p44 把代码放到一个main函数中，用GDB单步跟踪一下

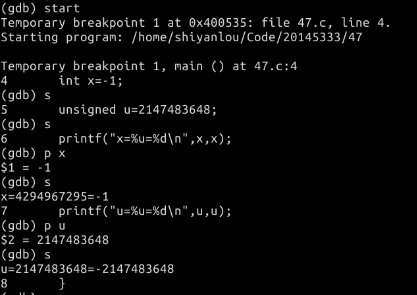
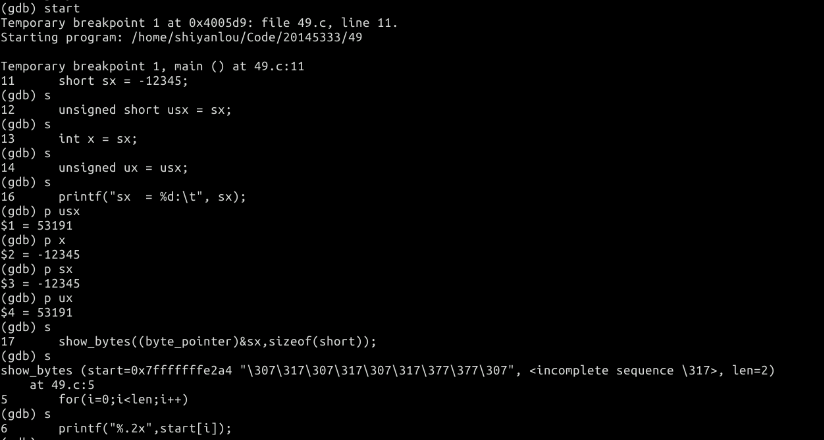
• p47/p49 代码放到一个main函数中，用GDB单步跟踪

教材学习中的问题和解决过程

1. p28代码出现了下面的问题，试了很多地方，还是没有解决，可是用VS就可以，不知道怎么弄。

家庭作业

• 2.56
  

• 2.64

  int any_even_one(unsigned x)
  {     
  return !!(x & (0x55555555));
  }

本周代码托管截图

代码地址：
http://git.oschina.net/20145333/Linux/tree/week3