图像漫画风格化算法研究

XDoG: An eXtended difference-of-Gaussians compendium including advanced image stylization

Holger Winnemoller，Jan Eric Kyprianidis，Sven C. Olsen

Adobe Systems, Inc.

Hasso-Plattner-Institut

        本文介绍一种将图像漫画风格化(黑白漫画)的算法。对于一幅图像，如果想要得到其对应的漫画风格或者素描风格的图像，则本文所介绍的算法是一种很好的选择。在介绍该算法之前，首先需要了解相关算子及其之间的关系，下面将占用一定的篇幅对其进行介绍。

        在该算法中，用到了LoG算子和DoG算子，在介绍这两个算子之前，首先介绍高斯核函数，我们知道一般的一维高斯函数可定义成如下形式：

        令，则变形为：

        将该函数在区间上积分，并将其用于给数据不均匀加权时，我们希望所有的权重之和为1，即：

        根据上式，可计算得到a的值，则可得到归一化的高斯核函数为：

        当使用高斯函数进行图像模糊处理时，很显然一维高斯核函数并不能满足需求。因此需要对一维高斯核函数进行拓展，获得二维高斯核函数。定义归一化二维高斯核函数为：

       将该函数在上进行积分，可得：

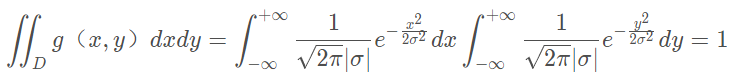
       利用高斯核函数可进行高斯滤波的操作对图像进行模糊处理或者去噪。我们经常使用均值滤波等滤波方法对图像进行去噪，但是均值滤波时，窗口中每个像素灰度值所取得的权重均是均等的，这种滤波的方法有时并不科学，因此可采用高斯滤波的方法得到更好的去噪效果。

       在介绍完高斯核函数后，在此需要介绍LoG算子：图像中的边缘，角点，拐点都可以称之为图像的特征点。那么如何求出这些点的位置呢？Laplacian算子利用求取图像的二阶微分极值点来获取图像的边缘，可以很好地解决这个问题。二阶微分定义如下：

 但是由于Laplacian算子对噪声敏感，因此首先利用二维高斯核函数对图像进行模糊去噪，然后求二阶微分极值点来获取图像中的边缘位置，可得：

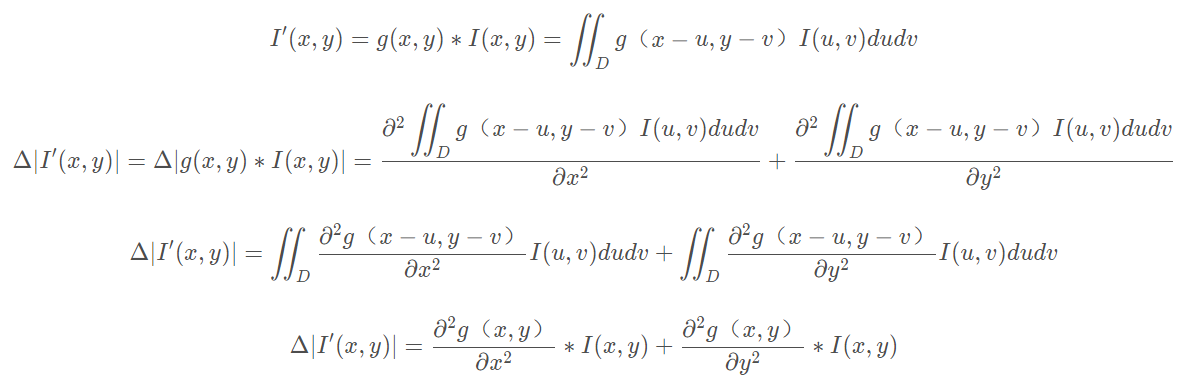
       根据卷积结合定律，可得：

       由(1)式可知，对图像进行高斯核函数卷积再求二阶微分等价于对高斯核函数先求二阶微分再用该核与图像进行卷积。定义LoG算子为二阶微分后的高斯核函数：

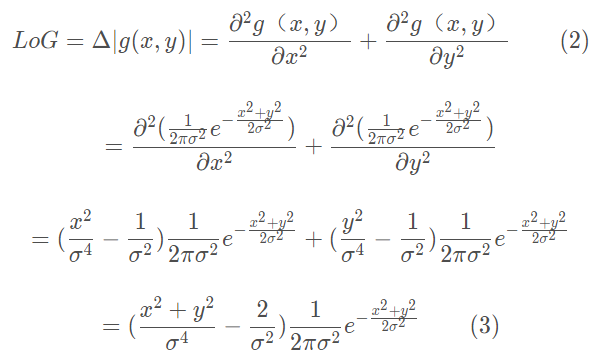
     又有归一化二维高斯核函数为：

     对该函数关于求导，可得：

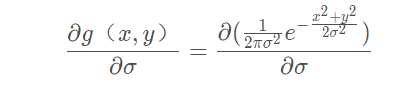
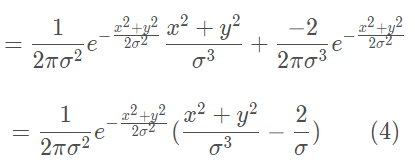
       观察(3)式和(4)式，发现其在结果上只差一个常数，即：

       下面介绍DoG算子，二维高斯核函数定义为：

       显然，其也是关于的函数，因而将其写成如下形式：

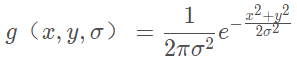
       此时，给出DoG算子的定义公式为：

       又由导数定义，可得高斯核函数关于的偏导数计算为：

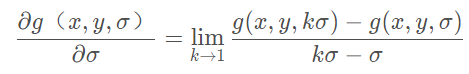
       故而对于给定常数，有如下近似：

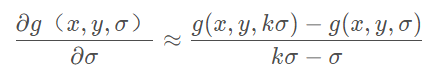
       联合(5)式，可得LoG与DoG之间的近似关系为：

       故而可得结论：LoG算子与DoG算子之间的形状相似，只在数值上相差常数，而DoG算子的运行速度远远快于LoG算子，所以可以使用DoG算子替代LoG算子求取图像的边缘信息。

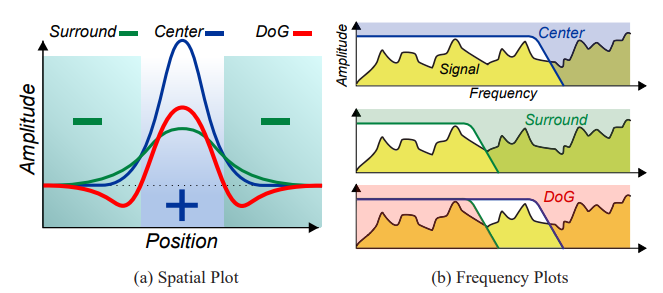
       对于DoG算子，下图(a)中蓝色曲线表示，绿色曲线表示，则两者之差得到的红色曲线表示DoG算子。下图(b)第一条和第二条频率-幅度曲线分别对应于函数和，则第三条频率-幅度曲线对应于两个函数之间的差值，即DoG算子。由DoG算子的频率-幅度曲线来看，其相当于一个带通滤波器。而我们想要得到一幅图像的明显而清晰的形状和结构，则需要对DoG算子处理后的图像作进一步的图像边缘增强，即对图像的DoG滤波相应设定阈值。

       若设定简单的单个阈值以增强DoG滤波图像得到DoG滤波边缘增强图像，则设定阈值的公式如下：

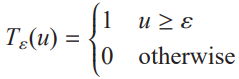
其中，参数用以控制对噪声的敏感程度。

       若按照上述定义的DoG算子及其阈值的设定过程，则过于简单粗暴，理想的处理效果往往不能够达到。因此引入参数以获得更多可变的漫画风格化效果，引入该参数后修正的DoG算子如下：

 则对于该修正后的DoG算子，也应该有相应的阈值函数与之匹配，该阈值函数为：

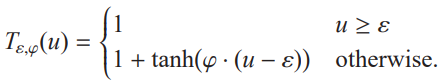
 则最后得到的图像即为针对输入图像的XDoG滤波结果图像，由此则可达到对图像进行漫画风格化的效果。

         下面给出该算法的C++代码，主要需要配置OpenCV，代码如下：

#include <iostream>
#include <vector>
#include <string>
#include <cmath>

#include <opencv2/opencv.hpp>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>

using namespace std;
using namespace cv;

void SeparateGaussianFilt(const vector<vector<double>>& src, vector<vector<double>>& dst, const double& sigma);

void SeparateGaussianFilt(const vector<vector<double>>& src, vector<vector<double>>& dst, const double& sigma)
{
    vector<double> kernel;
    double filterSize = 2 * ceil(2 * sigma) + 1;
    double filterRadius = (filterSize - 1) / 2;
    double sum = 0.0;

    for (int i = 0; i < filterSize; ++i)
    {
        double g = exp(-(pow((i - filterRadius), 2)) / (2 * sigma * sigma));
        kernel.push_back(g);
        sum += g;
    }

    for (int i = 0; i < kernel.size(); i++)
    {
        kernel[i] = double(kernel[i] / sum);
    }

    int a = src.size() + (2 * filterRadius); 
    int b = src[0].size() + (2 * filterRadius);

    vector<vector<double>> newSrc(a);

    for (int i = 0; i < a; i++)
    {
        newSrc[i].resize(b);
    }

    for (int i = 0; i < filterRadius; i++)
    {
        for (int j = 0; j < (b - 2 * filterRadius); j++)
        {
            newSrc[i][filterRadius + j] = src[0][j];
        }
    }

    for (int i = (a - filterRadius); i < a; i++)
    {
        for (int j = 0; j < (b - 2 * filterRadius); j++)
        {
            newSrc[i][filterRadius + j] = src[a - (2 * filterRadius) - 1][j];
        }
    }

    for (int i = filterRadius; i < a - filterRadius; i++)
    {
        for (int j = filterRadius; j < b - filterRadius; j++)
        {
            newSrc[i][j] = src[i - filterRadius][j - filterRadius];
        }
    }

    for (int i = 0; i < a; i++)
    {
        for (int j = 0; j < filterRadius; j++)
        {
            newSrc[i][j] = newSrc[i][filterRadius];
        }
    }

    for (int i = 0; i < a; i++)
    {
        for (int j = (b - filterRadius); j < b; j++)
        {
            newSrc[i][j] = newSrc[i][b - filterRadius - 1];
        }
    }

    for (int i = filterRadius; i < src.size() + filterRadius; i++)
    {
        for (int j = filterRadius; j < src[0].size() + filterRadius; j++)
        {
            double sum = 0.0;
            for (int r = (-filterRadius); r <= filterRadius; r++)
            {
                sum = sum + newSrc[i][j + r] * kernel[r + filterRadius];
            }
            dst[i - filterRadius][j - filterRadius] = sum;
        }
    }

    for (int i = 0; i < filterRadius; i++)
    {
        for (int j = 0; j < (b - 2 * filterRadius); j++)
        {
            newSrc[i][filterRadius + j] = dst[0][j];
        }
    }

    for (int i = (a - filterRadius); i < a; i++)
    {
        for (int j = 0; j < (b - 2 * filterRadius); j++)
        {
            newSrc[i][filterRadius + j] = dst[a - (2 * filterRadius) - 1][j];
        }
    }

    for (int i = filterRadius; i < a - filterRadius; i++)
    {
        for (int j = filterRadius; j < b - filterRadius; j++)
        {
            newSrc[i][j] = dst[i - filterRadius][j - filterRadius];
        }
    }

    for (int i = 0; i < a; i++)
    {
        for (int j = 0; j < filterRadius; j++)
        {
            newSrc[i][j] = newSrc[i][filterRadius];
        }
    }

    for (int i = 0; i < a; i++)
    {
        for (int j = (b - filterRadius); j < b; j++)
        {
            newSrc[i][j] = newSrc[i][b - filterRadius - 1];
        }
    }

    for (int i = filterRadius; i < src.size() + filterRadius; i++)
    {
        for (int j = filterRadius; j < src[0].size() + filterRadius; j++)
        {
            double sum = 0.0;
            for (int r = (-filterRadius); r <= filterRadius; r++)
            {
                sum = sum + newSrc[i + r][j] * kernel[r + filterRadius];
            }
            dst[i - filterRadius][j - filterRadius] = sum;
        }
    }
}


int main()
{
    Mat img = imread("xxx.jpg");

    imshow("image", img);

    Mat YCbCr, Y, Cr, Cb;
    vector<Mat> channels;
    cvtColor(img, YCbCr, CV_BGR2YCrCb);
    split(YCbCr, channels);

    Y = channels.at(0); Cr = channels.at(1); Cb = channels.at(2);

    Mat img_float;
    Y.convertTo(img_float, CV_64FC1, 1.0 / 255.0, 0);

    //参数中 k=1.6为定值
    double gamma = 0.96; double phi = 12.0; double epsilon = -0.1; double k = 1.6; double sigma = 1.0;

    int r = img_float.rows; 
    int c = img_float.cols;

    vector<vector<double>> img_vec(r);
    vector<vector<double>> dst(r); 
    vector<vector<double>> dst_k(r);

    for (int i = 0; i < r; i++)
    {
        img_vec[i].resize(c); dst[i].resize(c); dst_k[i].resize(c);
    }

    for (int i = 0; i < r; i++)
    {
        for (int j = 0; j < c; j++)
        {
            img_vec[i][j] = img_float.at<double>(i, j);
        }
    }

    SeparateGaussianFilt(img_vec, dst, sigma);
    SeparateGaussianFilt(img_vec, dst_k, sigma * k);

    Mat dst_mat(r, c, CV_64FC1); Mat dst_k_mat(r, c, CV_64FC1);

    for (int i = 0; i < r; i++)
    {
        for (int j = 0; j < c; j++)
        {
            dst_mat.at<double>(i, j) = dst[i][j];
            dst_k_mat.at<double>(i, j) = dst_k[i][j];
        }
    }

    dst_mat.convertTo(dst_mat, CV_64FC1, 1.0, 0);
    dst_k_mat.convertTo(dst_k_mat, CV_64FC1, 1.0, 0);

    Mat difference = Mat::zeros(r, c, CV_64FC1);

    for (unsigned int i = 0; i < r; i++)
    {
        const double* dst_Ptr = dst_mat.ptr<double>(i);
        const double* dst_k_Ptr = dst_k_mat.ptr<double>(i);
        double* diff_Ptr = difference.ptr<double>(i);
        for (unsigned int j = 0; j < c; j++)
        {
            *diff_Ptr = *dst_Ptr - *dst_k_Ptr * gamma;
            diff_Ptr++; dst_Ptr++; dst_k_Ptr++;
        }
    }

    Mat differenceimg = Mat::zeros(r, c, CV_64FC1);

    for (unsigned int i = 0; i < r; i++)
    {
        const double* diff_Ptr = difference.ptr<double>(i);
        double* diffimg_Ptr = differenceimg.ptr<double>(i);
        for (unsigned int j = 0; j < c; j++)
        {
            if (*diff_Ptr < epsilon) *diffimg_Ptr = 1.0;
            else *diffimg_Ptr = 1.0 + tanh(*diff_Ptr * phi);
            diff_Ptr++; diffimg_Ptr++;
        }
    }

    normalize(differenceimg, differenceimg, 1.0, 0.0, NORM_MINMAX);

    Mat diffimg = Mat::zeros(r, c, CV_8UC1);
    differenceimg.convertTo(diffimg, CV_8UC1, 255, 0);

    //imwrite("diffimg.jpg", diffimg);

    Scalar ave = mean(differenceimg);
    double meanVal = ave.val[0];

    Mat diffthresh = Mat::zeros(r, c, CV_64FC1);

    for (unsigned int i = 0; i < r; i++)
    {
        const double* diffimg_Ptr = differenceimg.ptr<double>(i);
        double* diffthresh_Ptr = diffthresh.ptr<double>(i);
        for (unsigned int j = 0; j < c; j++)
        {
            if (*diffimg_Ptr < meanVal) *diffthresh_Ptr = 0.0;
            else *diffthresh_Ptr = 1.0;
            diffimg_Ptr++; diffthresh_Ptr++;
        }
    }

    normalize(diffthresh, diffthresh, 1.0, 0.0, NORM_MINMAX);

    Mat filresult = Mat::zeros(r, c, CV_8UC1);
    diffthresh.convertTo(filresult, CV_8UC1, 255, 0);
    imwrite("result.jpg", filresult);

    imshow("result", filresult);

    waitKey(0);
    return 0;
}

        下面给出几组测试结果，以证明该算法的有效性，可得到其黑白漫画风格的处理结果图像。