基于瑞利模型的E矢量叉乘太阳方位角解算方法
太阳光在其传播过程中由于受到大气层中空气分子、气溶胶粒子等的散射作用,以及地表植被、水面等的反射作用而产生了偏振光。虽然人类的视觉无法直接感知偏振光,但许多生物如沙蚁、蜜蜂、蝗虫等昆虫,甚至大耳蝙蝠,却能够利用其独特的视觉结构,感知并利用光的偏振现象获取信息,从而进行导航、觅食、交流、迁徙等活动。一系列的解剖生物学研究证明,部分生物具有偏振光导航能力是依靠其复眼中特殊的偏振神经感光结构能够对快速变化的大气偏振模式信息进行检测和处理,从而提取可靠的罗盘信息进行导航。这一研究结果为仿生偏振光导航提供了生物基础,开辟了基于仿生的偏振光导航的研究方向。
大气偏振模式是天空中的偏振光最终形成的具有一定规律的偏振态分布,其中蕴含重要的方向信息。生物研究表明,沙蚁、蜜蜂等昆虫的导航不是应用天空单点的大气偏振模式信息,而是利用整个或局部具有稳定分布的大气偏振模式信息,并从中提取体轴与太阳子午线的夹角,从而实现导航功能。因此,利用大气偏振模式有效获取作为天空显著点的太阳位置信息,就可以为导航提供参考基准,是实现偏振光导航的前提和关键技术,同时,也对太阳位置追踪和利用有着重要的意义。
大气偏振模式的瑞利表征方法:晴朗天气情况下,大气粒子对光的散射过程,满足瑞利散射条件,因此可通过瑞利散射理论得到大气偏振模式的表征。瑞利表征认为太阳光在天球表面上的各点位置同大气粒子发生一次散射后,即被观测者接收,这能准确描述在理想条件下大气中光纤呈现的分布特征,是应用最为广泛的一种表征方法。而大气偏振模式则可看成是大气中各个点一次散射作用的集合效应。瑞利散射模型是现有描述理想条件下大气偏振模式最为经典的表征方法,与实际大气偏振模式具有较高的相似性,通常使用偏振度(DOP)和偏振角度(AOP,也称E-矢量方向)来描述,下图给出了大气偏振模式的瑞利表征建模坐标系。图中,观测者为原点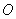 ,太阳位置为
,太阳位置为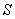 ,天定点为
,天定点为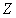 ,向天顶方向为
,向天顶方向为 轴,正东方向为
轴,正东方向为 轴,正北方向为
轴,正北方向为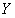 轴。球面上任意一点
轴。球面上任意一点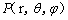 的天顶角为
的天顶角为 ,方位角为
,方位角为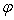 ,
,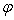 以正北方向为0,正北往东为正值。太阳空间位置表示为
以正北方向为0,正北往东为正值。太阳空间位置表示为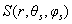 ,其中,
,其中, 表示太阳天顶角,
表示太阳天顶角, 表示太阳方位角,太阳的高度角为
表示太阳方位角,太阳的高度角为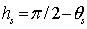 ,太阳子午线在地理坐标系中的位置以方位角
,太阳子午线在地理坐标系中的位置以方位角 来表示。
来表示。

偏振化方向角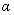 定义为被测点
定义为被测点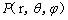 处E-矢量方向同所在子午线夹角,根据瑞利散射定律,任一被测点
处E-矢量方向同所在子午线夹角,根据瑞利散射定律,任一被测点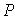 处的E-矢量为:
处的E-矢量为:
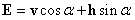
其中,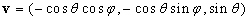 ,
,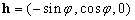 。
。
当太阳位置坐标在三维坐标下表示为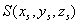 ,其高度角为
,其高度角为 ,方位角为
,方位角为 时,可以获得天空中任意一点
时,可以获得天空中任意一点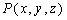 ,高度角为
,高度角为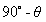 ,方位角为
,方位角为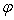 时的偏振化方向角
时的偏振化方向角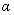 的理论值为:
的理论值为:
 下图表示瑞利模型下的几种坐标系之间的关系,包括地理坐标系、相机坐标系、入射光坐标系。图中,
下图表示瑞利模型下的几种坐标系之间的关系,包括地理坐标系、相机坐标系、入射光坐标系。图中,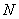 表示地理北,
表示地理北,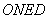 表示地理坐标系,
表示地理坐标系,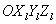 表示相机坐标系,
表示相机坐标系, 表示入射光坐标系,
表示入射光坐标系, 与
与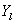 分别与图像的横纵坐标轴平行,
分别与图像的横纵坐标轴平行,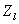 与相机平面垂直,指向天顶点;
与相机平面垂直,指向天顶点;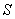 表示太阳位置,
表示太阳位置,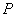 表示观测点,
表示观测点, 与
与 分别为太阳位置
分别为太阳位置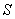 在地理坐标系中的天顶角和方位角,
在地理坐标系中的天顶角和方位角, 与
与 分别为观测点
分别为观测点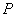 在相机坐标系
在相机坐标系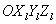 中的天顶角和方位角;
中的天顶角和方位角; 为在入射光坐标系中的E-矢量,该矢量与
为在入射光坐标系中的E-矢量,该矢量与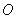 、
、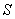 、
、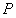 三点构成的平面垂直,由矢量
三点构成的平面垂直,由矢量 与矢量
与矢量 叉乘得到;入射光坐标系的
叉乘得到;入射光坐标系的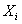 轴与E-矢量之间的夹角即为该处的偏振化方向角(简称偏振角)
轴与E-矢量之间的夹角即为该处的偏振化方向角(简称偏振角)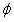 。
。

入射光坐标系中的E-矢量为关于偏振角 的函数,为求解E-矢量则首先应求解偏振角
的函数,为求解E-矢量则首先应求解偏振角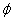 ,求解偏振角
,求解偏振角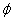 的步骤如下:首先获得晴朗天气下的天空图像,使用相机NiKon-D800拍摄
的步骤如下:首先获得晴朗天气下的天空图像,使用相机NiKon-D800拍摄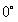 、
、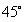 、
、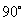 和
和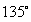 四个偏振角度的大气偏振图像,相机设备如下图所示,在相机镜头前安装鱼眼镜头,并在鱼眼镜头前放置偏振片,旋转偏振片至不同角度并拍摄以获取不同偏振角度的大气的偏振图像。
四个偏振角度的大气偏振图像,相机设备如下图所示,在相机镜头前安装鱼眼镜头,并在鱼眼镜头前放置偏振片,旋转偏振片至不同角度并拍摄以获取不同偏振角度的大气的偏振图像。

拍摄得到的四幅不同角度的大气偏振图像如下,拍摄时间为2019年6月27日19点04分,从左至右的偏振图像的角度分别为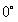 、
、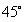 、
、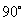 和
和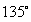 。(实验时获取了同一天的其他多组实验数据,为了便于描述算法,本文仅举一组数据为例。)
。(实验时获取了同一天的其他多组实验数据,为了便于描述算法,本文仅举一组数据为例。)




设四幅偏振图像的光强分别为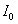 、
、 、
、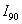 和
和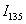 ,由此计算该偏振态下的斯托克斯矢量分量
,由此计算该偏振态下的斯托克斯矢量分量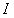 、
、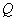 、
、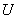 :
:
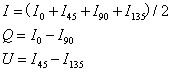
由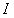 、
、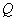 、
、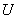 计算每一个像素
计算每一个像素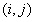 处的偏振角为:
处的偏振角为:
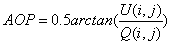
重绘 图,使其沿着太阳子午线中心反对称且呈∞字形分布,计算公式为:
图,使其沿着太阳子午线中心反对称且呈∞字形分布,计算公式为:

设天空中不同观测点位置对应像素中的两个坐标分别为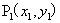 和
和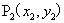 ,则两个坐标对应的天顶角和方位角分别为:
,则两个坐标对应的天顶角和方位角分别为:

其中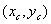 为图像的中心位置的坐标,
为图像的中心位置的坐标, 为相机的焦距。
为相机的焦距。
偏振角图像中 ,
, 处的像素灰度值
处的像素灰度值 ,
,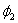 为该两观测点处的散射光的偏振角的值,则在入射光坐标系
为该两观测点处的散射光的偏振角的值,则在入射光坐标系 中表示E-矢量为:
中表示E-矢量为:

在三维空间的坐标系为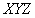 ,绕三个坐标轴其中一轴旋转得到新的坐标系,则原先坐标系中的点用旋转后的坐标系表示时,点的坐标转换关系如下:
,绕三个坐标轴其中一轴旋转得到新的坐标系,则原先坐标系中的点用旋转后的坐标系表示时,点的坐标转换关系如下:
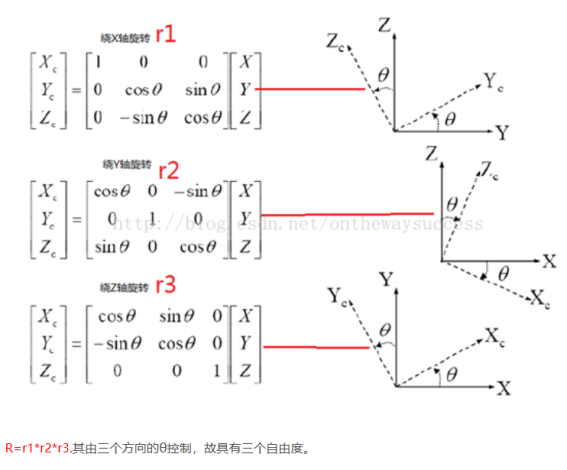
为了计算太阳矢量,需要将E-矢量从入射光坐标系转换到相机坐标系。若要将入射光坐标系转化到相机坐标系,需要将入射光坐标系旋转两次:将入射光坐标系 绕
绕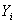 轴向上旋转
轴向上旋转 角度,得到新的坐标系
角度,得到新的坐标系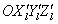 ;将坐标系
;将坐标系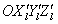 绕
绕 轴(
轴(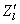 轴与
轴与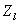 轴重合)向右旋转
轴重合)向右旋转 角度,得到相机坐标系
角度,得到相机坐标系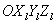 。每旋转一次坐标系,左乘对应的旋转矩阵,旋转矩阵中的角度对应于坐标轴旋转的角度,由此可得入射光坐标系到相机坐标系的坐标转换矩阵为:
。每旋转一次坐标系,左乘对应的旋转矩阵,旋转矩阵中的角度对应于坐标轴旋转的角度,由此可得入射光坐标系到相机坐标系的坐标转换矩阵为:
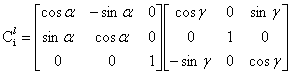
则将 ,
, 处的E-矢量在相机坐标系中表示为:
处的E-矢量在相机坐标系中表示为:
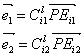
由任意两个E-矢量叉乘得到太阳矢量的规律,可表示太阳矢量为:
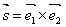
上述计算太阳矢量时,选取一对像素处的E-矢量叉乘得到太阳矢量,这样只进行一次运算得到的结果误差太大,需要选取多组E-矢量叉乘得到一组太阳矢量,对这组太阳矢量利用最小二乘法求解方位角,这样得到的结果更加准确。
利用最小二乘法求解方位角:设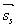 为所求太阳矢量,设矩阵
为所求太阳矢量,设矩阵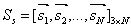 由向量
由向量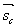 构成(
构成( )。构造损失函数为:
)。构造损失函数为:

其中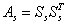 为3x3的对称矩阵。
为3x3的对称矩阵。
利用拉格朗日乘数法求解上述损失函数,定义函数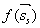 为:
为:
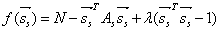
对函数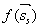 关于
关于 求导,可得:
求导,可得:

其中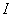 为3x3的单位矩阵,
为3x3的单位矩阵,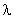 为矩阵
为矩阵 的特征值。由于
的特征值。由于 为非零向量,故当
为非零向量,故当 为0时,有
为0时,有 。
。
将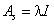 代入到
代入到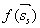 中,可得:
中,可得:
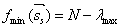
所以损失函数的最优解对应于矩阵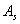 的最大特征值的特征向量,该特征向量即为所求的太阳矢量
的最大特征值的特征向量,该特征向量即为所求的太阳矢量 ,则有方位角
,则有方位角 为:
为:
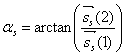
本例中选取相机坐标系的 轴和地理北极
轴和地理北极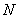 重合,所以航向角
重合,所以航向角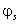 满足:
满足: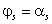 或者
或者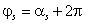 。
。
上述算法的C++程序如下给出,在VS2017搭配opencv3.4.1环境下运行,另需配置Eigen库:
#include <iostream> #include <stdlib.h> #include <time.h> #include <cmath> #include <algorithm>
#include <opencv2\opencv.hpp> #include <opencv2\core.hpp> #include <opencv2\highgui.hpp> #include <opencv2\imgproc.hpp> #include <Eigen\core> #include <Eigen\Dense> #include <opencv2\core\eigen.hpp> using namespace cv; using namespace std; typedef std::numeric_limits<double> Info; double const NAN_d = Info::quiet_NaN(); void Vector2Mat(vector<vector<double>>src, Mat dst); void cv_to_eigen(const Mat& input, Eigen::Matrix3d& output); int main() { string loc1 = "E:\\sunvector\\sunvector\\0.JPG"; string loc2 = "E:\\sunvector\\sunvector\\45.JPG"; string loc3 = "E:\\sunvector\\sunvector\\90.JPG"; string loc4 = "E:\\sunvector\\sunvector\\135.JPG"; Mat src1 = imread(loc1); Mat src2 = imread(loc2); Mat src3 = imread(loc3); Mat src4 = imread(loc4); src1.convertTo(src1, CV_64FC3, 1.0, 0); src2.convertTo(src2, CV_64FC3, 1.0, 0); src3.convertTo(src3, CV_64FC3, 1.0, 0); src4.convertTo(src4, CV_64FC3, 1.0, 0);
int x1, x2, y1, y2; //(x1, y1)和(x2, y2)为裁剪有效矩形区域的左上角坐标和右下角坐标
int rr, oo, dd; //rr为裁剪有效矩形区域中圆的圆心,oo为圆的半径,dd为圆的直径 Mat image0 = src1(Rect(Point(x1, y1), Point(x2, y2))); Mat image45 = src2(Rect(Point(x1, y1), Point(x2, y2))); Mat image90 = src3(Rect(Point(x1, y1), Point(x2, y2))); Mat image135 = src4(Rect(Point(x1, y1), Point(x2, y2))); vector<Mat> planes0; split(image0, planes0); Mat I0 = (planes0[0] + planes0[1] + planes0[2]) / 3; vector<Mat> planes45; split(image45, planes45); Mat I45 = (planes45[0] + planes45[1] + planes45[2]) / 3; vector<Mat> planes90; split(image90, planes90); Mat I90 = (planes90[0] + planes90[1] + planes90[2]) / 3; vector<Mat> planes135; split(image135, planes135); Mat I135 = (planes135[0] + planes135[1] + planes135[2]) / 3; Mat I = (I0 + I45 + I90 + I135) / 2; Mat Q = I0 - I90; Mat U = I45 - I135; int rows = I.rows; int cols = I.cols; double PI = 3.1415926; Mat aop(rows, cols, CV_64FC1); for (unsigned int i = 0; i < rows; i++) { const double* Qptr = Q.ptr<double>(i); const double* Uptr = U.ptr<double>(i); double* aopPtr = aop.ptr<double>(i); for (unsigned int j = 0; j < cols; j++) { *aopPtr = (0.5 * atan2(*Uptr, *Qptr)) * (180 / PI); aopPtr++; Uptr++; Qptr++; } } Mat aop_last = Mat::zeros(rows, cols, CV_64FC1); for (unsigned int i = 0; i < rows; i++) { const double* aopPtr = aop.ptr<double>(i); double* aop_lastPtr = aop_last.ptr<double>(i); for (unsigned int j = 0; j < cols; j++) { double x = i; double y = j; if (j == oo) { *aop_lastPtr = *aopPtr + (PI / 2) * (180 / PI); } else { *aop_lastPtr = *aopPtr - (atan((x - oo) / (oo - y))) * (180 / PI); if (*aop_lastPtr < -90) { *aop_lastPtr = 180 + *aop_lastPtr; } else if (*aop_lastPtr > 90) { *aop_lastPtr = *aop_lastPtr - 180; } } aopPtr++; aop_lastPtr++; } } Mat aop_circle = Mat::zeros(rows, cols, CV_64FC1); for (unsigned int i = 0; i < rows; i++) { const double* aop_lastPtr = aop_last.ptr<double>(i); double* aop_circlePtr = aop_circle.ptr<double>(i); for (unsigned int j = 0; j < cols; j++) { if ((i - oo) * (i - oo) + (j - oo) * (j - oo) < rr * rr) { *aop_circlePtr = *aop_lastPtr; } else { *aop_circlePtr = NAN_d; } aop_lastPtr++; aop_circlePtr++; } } Mat aop_color; Mat aop_show = Mat::zeros(rows, cols, CV_64FC3); double min_aop, max_aop, alpha_aop; minMaxLoc(aop_circle, &min_aop, &max_aop); Mat aop_circle1 = aop_circle; alpha_aop = 255.0 / (max_aop - min_aop); aop_circle1.convertTo(aop_circle1, CV_8U, alpha_aop, -min_aop * alpha_aop); applyColorMap(aop_circle1, aop_color, COLORMAP_JET); imwrite("aop.bmp", aop_color); string aop_map1 = "E:\\sunvector\\sunvector\\aop.bmp"; Mat aop_map = imread(aop_map1); aop_map.convertTo(aop_map, CV_64FC3, 1 / 255.0, 0); //imshow("aop",aop_map); vector<Mat> channels(3); split(aop_map, channels); for (unsigned int i = 0; i < rows; i++) { const double* channel0Ptr = channels[0].ptr<double>(i); const double* channel1Ptr = channels[1].ptr<double>(i); const double* channel2Ptr = channels[2].ptr<double>(i); double* aop_showPtr = aop_show.ptr<double>(i); for (unsigned int j = 0; j < cols; j++) { if ((i - oo)*(i - oo) + (j - oo)*(j - oo) < rr * rr) { *aop_showPtr++ = *channel0Ptr; *aop_showPtr++ = *channel1Ptr; *aop_showPtr++ = *channel2Ptr; } else { *aop_showPtr++ = 1; *aop_showPtr++ = 1; *aop_showPtr++ = 1; } channel0Ptr++; channel1Ptr++; channel2Ptr++; } } imshow("aop_show",aop_show); aop_show.convertTo(aop_show, CV_8UC3, 255.0, 0); imwrite("aop_save.bmp", aop_show); int amount = 10000; int q = 0; vector<vector<double>> Su; for (unsigned int inter = 0; inter < amount; inter++) { int i1 = rand() % (rows - 1); int j1 = rand() % (cols - 1); int i2 = rand() % (rows - 1); int j2 = rand() % (cols - 1); if (((i1 - oo) * (i1 - oo) + (j1 - oo) * (j1 - oo) < rr * rr) && ((i2 - oo) * (i2 - oo) + (j2 - oo) * (j2 - oo) < rr * rr)) { q++; double x1 = i1 - oo; double y1 = j1 - oo; double x2 = i2 - oo; double y2 = j2 - oo; double k1 = (aop_circle.at<double>(i1, j1)) * (PI / 180); double k2 = (aop_circle.at<double>(i2, j2)) * (PI / 180); double b1 = atan(y1 / x1); double b2 = atan(y2 / x2); double a1 = atan(sqrt(x1 * x1 + y1 * y1) * (0.0087 / 8)); double a2 = atan(sqrt(x2 * x2 + y2 * y2) * (0.0087 / 8)); Eigen::Matrix<double, 3, 3> C11; Eigen::Matrix<double, 3, 3> C12; C11 << cos(a1), 0, -sin(a1), 0, 1, 0, sin(a1), 0, cos(a1); C12 << cos(b1), sin(b1), 0, -sin(b1), cos(b1), 0, 0, 0, 1; Eigen::Matrix<double, 3, 3> Cli1 = C11 * C12; Eigen::Matrix<double, 3, 3> C21; Eigen::Matrix<double, 3, 3> C22; C21 << cos(a2), 0, -sin(a2), 0, 1, 0, sin(a2), 0, cos(a2); C22 << cos(b2), sin(b2), 0, -sin(b2), cos(b2), 0, 0, 0, 1; Eigen::Matrix<double, 3, 3> Cli2 = C21 * C22; Eigen::Matrix<double, 1, 3> PEi1; Eigen::Matrix<double, 1, 3> PEi2; PEi1 << cos(k1), sin(k1), 0; PEi2 << cos(k2), sin(k2), 0; Eigen::Matrix<double, 1, 3> e1 = PEi1 * Cli1; Eigen::Matrix<double, 1, 3> e2 = PEi2 * Cli2; Eigen::Vector3d Evec1 = Eigen::Vector3d(e1(0, 0), e1(0, 1), e1(0, 2)); Eigen::Vector3d Evec2 = Eigen::Vector3d(e2(0, 0), e2(0, 1), e2(0, 2)); Eigen::Vector3d S0 = Evec1.cross(Evec2); double normS0 = sqrt(S0[0] * S0[0] + S0[1] * S0[1] + S0[2] * S0[2]); Eigen::Vector3d S = S0 / normS0; vector<double> s(3); s[0] = S[0]; s[1] = S[1]; s[2] = S[2]; Su.push_back(s); if (q > 999) { break; } } } Mat Smat(Su.size(), 3, CV_64FC1); Vector2Mat(Su, Smat); Mat S1; S1 = (Smat.t()) * Smat; Eigen::Matrix3d SunMat; cv_to_eigen(S1, SunMat); Eigen::JacobiSVD<Eigen::Matrix3d> svd(SunMat, Eigen::ComputeFullU | Eigen::ComputeFullV); Eigen::Vector3d SigularVal = svd.singularValues(); Eigen::Matrix3d V = svd.matrixV(); Eigen::Vector3d SunVector = Eigen::Vector3d(V(0, 0), V(1, 0), V(2, 0)); double posAngle = atan2(SunVector(1), SunVector(0)) * (180 / PI); cout << "The orientation angle is:" << posAngle << " degree" << endl; waitKey(0); return 0; } void Vector2Mat(vector<vector<double>>src, Mat dst) { assert(dst.rows == src.size()); MatIterator_<double> it = dst.begin<double>(); for (int i = 0; i < src.size(); i++) { for (int j = 0; j < src[0].size(); j++) { *it = src[i][j]; it++; } } } void cv_to_eigen(const Mat& input, Eigen::Matrix3d& output) { cv2eigen(input, output); }
由于瑞利模型是光进行一次散射的理想化模型,而真实的大气偏振模式是多次散射的结果,所以为了提高计算精度,选取图像的中心区域(半径为200个像素)作为像素取样板。在所选中心图像区域中,任意选取两个像素对应的E-矢量叉乘得到太阳矢量,这样取点次数越多,计算精度越高,本次实验选取1000对像素。本次实验运行得到的AOP图如下图所示:

计算得到的方位角为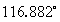 ,该夹角为AOP图中太阳子午线与地理北极之间的夹角,知道了这个夹角,就可以知道所在位置的方位,从而进行导航。为了衡量该计算结果的精度,应用SPA算法计算实验的时刻和地点时的准确的方位角。实验时间为2019年6月27日19点04分,将实验时间和实验地点经纬度代入到SPA算法中,计算得到此时此地的方位角为
,该夹角为AOP图中太阳子午线与地理北极之间的夹角,知道了这个夹角,就可以知道所在位置的方位,从而进行导航。为了衡量该计算结果的精度,应用SPA算法计算实验的时刻和地点时的准确的方位角。实验时间为2019年6月27日19点04分,将实验时间和实验地点经纬度代入到SPA算法中,计算得到此时此地的方位角为 ,则测量得到的方位角和实际的方位角之间的误差为
,则测量得到的方位角和实际的方位角之间的误差为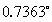 ,可见该组数据的计算结果已经达到很好的精度。但是,对于同一天的其余组数据,其计算得到的方位角误差较大,有的误差达到了5度到10度之间,可见该算法在计算太阳矢量时仍有较大缺陷。
,可见该组数据的计算结果已经达到很好的精度。但是,对于同一天的其余组数据,其计算得到的方位角误差较大,有的误差达到了5度到10度之间,可见该算法在计算太阳矢量时仍有较大缺陷。
误差较大的原因分析:无论怎么样,本文算法都是基于瑞利模型进行计算的,而瑞利模型仅仅是理想化的模型,即瑞利模型模拟的是光对粒子的单次散射的过程。而真实的情况是,大气偏振模式是光的多次散射的结果。因此,利用单次散射的瑞利模型描述实际上更加复杂的大气偏振模式是不符合实际的,基于此计算得到的方位角必然带来误差。(其实如果追求计算方位角的精度的话,利用偏振角图像关于太阳子午线对称的规律直接求解太阳子午线就完事了,这样计算的精度最高,且不需要依赖任何模型,但是这样做是没有任何意义的。)
本次实验中,计算得到的太阳矢量不仅可以计算得到太阳位置的方位角,也可计算得到太阳位置的高度角。但是本例计算得到的高度角误差较大,因此在不需要空间导航,仅在二维水平面中导航的情况下,本例基于E-矢量叉乘计算太阳矢量,从而计算航向角的方法是一种很好的基于物理意义的大气偏振光导航方案。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号