01背包问题

01背包问题

有10件商品，要从 甲地 运往 乙地，每件货的总量和利润如下表，求一辆最大载重为 30t 的货车，运输这些货物的总利润最大。答案是 ：2410

物品	1	2	3	4	5	6	7	8	9	10
总量	6	3	4	5	1	2	3	5	4	2
利润	540	200	180	350	60	150	280	450	320	120

定义原问题和子问题

分析思路

代码，下面的参考文献讲的很清楚

代码参考文献

// nums[0]表示重量，nums[1]表示价值
func backpack(nums [][]int, cap int) int { //nums表示体积和价值更容易理解

	// 创建dp数组,dp[i][j]表示将从前 i 件商品中，选取若干产品，放入容量为j的的背包中
	dp := make([][]int, len(nums))

	//初始化二维数组,多维切片必须逐个声明
	for i := 0; i < len(nums); i++ {
		dp[i] = make([]int, cap)
	}

	//放入第一个物品，填第一行列表
	for j := nums[0][0]; j < cap; j++ {
		dp[0][j] = nums[0][1] //nums[][0]表示体积，nums[][1]表示价值
	}

	for i := 1; i < len(nums); i++ {
		for j := nums[i][0]; j < cap; j++ {
			// 因为j是从 nums[i][0]开始的，所以一定能放进去，下面就考虑放还是不放
			// 这个东西如果放不进去，就不放了，价值就是 dp[i-1][j]
			// 如果放进去了，就相当于，除了这个包之外的空间，作为一个完整的包来对待
			dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i][0]]+nums[i][1])
		}
	}
	return dp[len(nums)-1][cap-1]
}

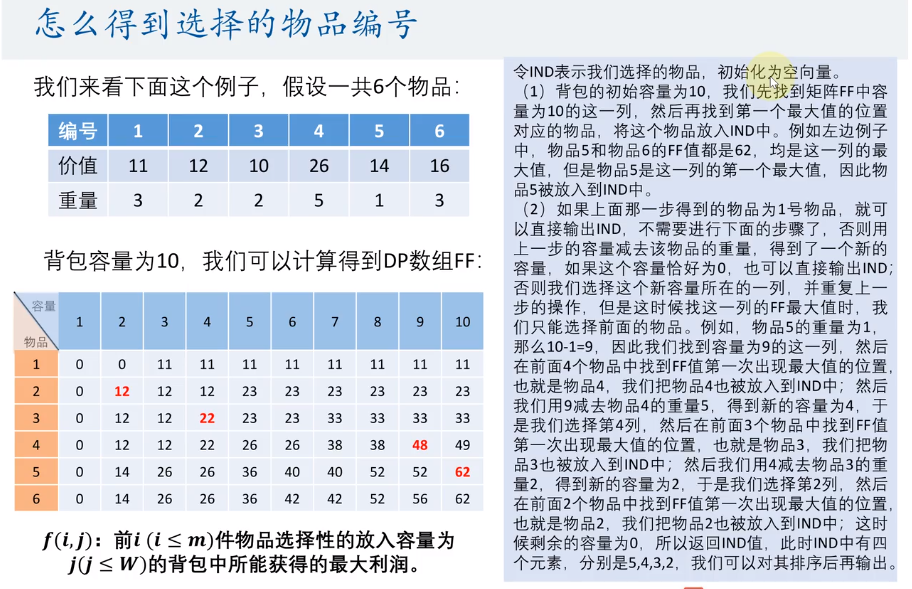
如何输出选择的顺序