动态规划问题
动态规划问题
动态规划（Dynamic Programming）（简称 DP 问题），是运筹学的一个分支，通常用来解决多阶段决策过程最优化问题，动态规划的基本思想，是将原问题，转化为一系列相互联系的子问题，然后通过逐层递推来求的最后的解。
斐波拉契数列
斐波拉契数列的样子
0 ,1, 1, 2, 3, 5, 8, 13
直接的自顶向下算法
func F(i int) int {
if i == 0 {
return 0
}
if i == 1 {
return 1
}
return F(i-1) + F(i-2)
}
带有备忘录的至顶向下算法
var memo map[int]int
func main() {
memo=make(map[int]int,50)
a := F(40)
fmt.Println(a)
}
func F(i int) int {
if v, ok := memo[i]; ok {
return v
}
if i == 0 {
return 0
}
if i == 1 {
return 1
}
f := F(i-1) + F(i-2)
memo[i] = f
return f
}
自底向上算法
想从小的算，逐渐的往大的上面推。
这种算法，其实更容易理解，而且更快。
func main() {
a := make([]int, 40)
a[0], a[1] = 0, 1
for i := 3; i < len(a); i++ {
a[i] = a[i-1] + a[i-2]
}
fmt.Println(a[39])
}
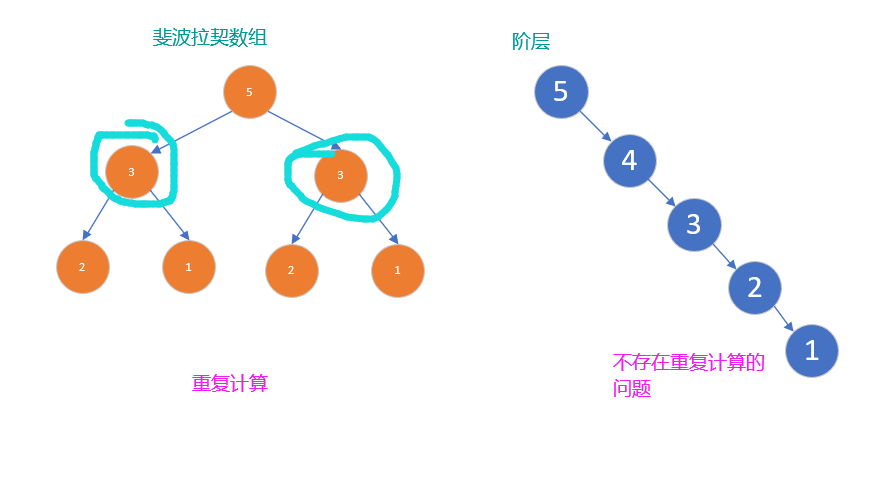
从斐波拉契数列，到动态规划
严格意义上来说，斐波拉契数列并不算是严格的 动态规划 ，因为动态规划一般是用来求解优化问题。
动态规划通过求解子问题来求解原问题，一般来说，动态规划应用于 重叠子问题 的情况，即不同的子问题，有相同的子子问题，动态规划算法，技术将每个问题，只求解一次，将其解存放在一个表格中，而不用每次求解，都再求一次子子问题。
思考题：递归是动态规划问题吗？
答案，不是，因为他没有牵扯到重复的子子问题。
动态规划中的常见概念
１.原问题和子问题
原文就是你本身要求解的问题，子问题就是和原问题相似，但是规模较小的问题。
不如求 F(10)，那么 F(10) 就是原问题 F(k) (k<10) 都是子问题
2.状态
状态就是子问题中会变化的某个量，可以把状态看成我们要求解问题的 自变量
例如我们要求的 F(10),10就是一个状态
3.状态转移方程
表示状态之间转移关系的方程，例如：F(n) = F(n-1) + F(n-2)。比如这种 n=1或者 n=2,时候 F(1)=1; F(0)=0 。一般这样的方程也称为是边界条件，也称为是 基准方程。
4.DP数组（动态规划数组）
DP数组也叫子问题数组，因为 DP 数组中，每一个元素，都对应一个子问题结果。DP数组的下标，一般就是该子问题对应的状态。
打家劫舍问题
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。
例一
输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
例二
输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
代码实现
自顶向下的写法
var a map[int]int
func rob(nums []int) int {
a = make(map[int]int, 20)
a[0] = nums[0]
a[1] = nums[1]
return F(len(nums)-1, nums)
}
func F(i int, nums []int) int {
if i == 0 {
return a[0]
}
if i == 1 {
return Max(a[0], a[1])
}
if v, ok := a[i]; ok {
return v
} else {
rel := Max(F(i-1, nums), F(i-2, nums)+nums[i])
a[i] = rel
return rel
}
}
func Max(a, b int) int {
if a > b {
return a
} else {
return b
}
}
使用自底而上的方法
func rob(nums []int) int {
maxmony := make([]int, len(nums))
maxmony[0] = nums[0]
maxmony[1] = max(nums[0], nums[1])// max是自定义求大小的函数
for i := 2; i < len(nums); i++ { //注意这个地方应该从2开始
// 注意最后一个是用什么加的
maxmony[i] = max(maxmony[i-1], maxmony[i-2]+nums[i])
}
return maxmony[len(nums)-1]
}
如何输出偷窃金额的房间号
在输出这一部分之前，我们应该先注意：产生最大偷窃金额的方案并不唯一，我们只需要输出任意一种方案即可，例如 M=【1,3,2】就有两种方案。
理解如何输出最大偷窃金额的房间号前，应该先理解如下结论
- 对于任意的 i 均有
maxmony[i]>nums[i]。 maxmony是一个递增数组。
我们通过一个例子，来说明这个问题
maxmony=[ 1, 4, 1, 2, 5, 6, 3 ]
nums= [ 1, 4, 4, 6, 9, 12, 12]
结果为: 12，顺序为（1,3,5）
实现代码
package main
import "fmt"
func main() {
s := []int{2, 7, 9, 3, 1}
a, b := rob(s)
fmt.Println(a, b)
}
func rob(nums []int) (int, []int) {
maxmoney := make([]int, len(nums))
maxmoney[0] = nums[0]
maxmoney[1] = max(nums[0], nums[1]) // max是自定义求大小的函数
for i := 2; i < len(nums); i++ { //注意这个地方应该从2开始
// 注意最后一个是用什么加的
maxmoney[i] = max(maxmoney[i-1], maxmoney[i-2]+nums[i])
}
// 根据 maxmony 和 nums 两个数组，推断出来，得出最优化的房间号
// maxmony = [ 2 7 11 11 12]
// nums = [ 2 7 9 3 1]
suq := []int{}
money := maxmoney[len(maxmoney)-1]
// 第一次出现最大值得时候，就是最后偷的房间
for i := len(nums) - 1; i >= 0; i-- {
if maxmoney[i] != maxmoney[i-1] {
suq = append(suq, i)
money -= nums[i]
}
if nums[i] == maxmoney[i] { //如果背包的东西和房间的东西一样，那么这就是最后一个房间。
break
}
}
return maxmoney[len(nums)-1], suq
}
func max(a, b int) int { //判断最大最小值
if a > b {
return a
} else {
return b
}
}
礼物的最大价值问题
在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？
解析：每个格子的单元格，只能由他上边单元格或者左边单元格到达。
定义原问题和子问题
原问题：从左上角开始，直到棋盘的右下角，所能获得最大礼物价值。
子问题： 从左上角开始，到棋盘的第 i 行，第 j 列，所能获得最大礼物价值。其中 0<=i<=m, 0<=j<=n,
定义状态
记 F(i,j)，表示棋盘从左上角开始，一直走到第 i,j行列，所获得最大礼物价值，这里即可认为是上述问题，所对应的状态。特别的，当 i=m,j=n的时候，该状态对应的 f(m,n) 就是我们所要求的原问题的答案。
代码
func maxValue(grid [][]int) int {
// 可以使用grid本身记录数据，降低空间复杂度
for i := 0; i < len(grid); i++ {
for j := 0; j < len(grid[i]); j++ {
if i == 0 && j != 0 {
grid[0][j] += grid[0][j-1]
continue
}
if j == 0 && i != 0 {
grid[i][0] += grid[i-1][0]
continue
}
if j != 0 && i != 0 {
grid[i][j] = Max(grid[i-1][j], grid[i][j-1]) + grid[i][j]
}
}
}
return grid[len(grid)-1][len(grid[0])-1]
}
func Max(a, b int) int {
if a > b {
return a
} else {
return b
}
}
输出最大的路线
同样的，此处的路线并不唯一
这个就很简单，我就不写了，提示：这个点是由他上面或者下面的数相加得来的，那么减去他本身，等于谁，他上一个值就是谁。
零钱兑换问题
给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。
你可以认为每种硬币的数量是无限的。
例如
输入：coins = [1, 2, 5], amount = 11
输出：3
解释：11 = 5 + 5 + 1
在例如
输入：coins = [2], amount = 3
输出：-1
分析
原问题和子问题
原问题： 凑成总金额 s 的最少硬币个数
子问题： 凑成目标金额 x 所需的最少硬币个数
总金额s，是一个会变的数，所以他是一个变量，他应该是状态，i，所以他有邻接条件，那么dp数组的dp[i]中的 i ，就应该对应的是金额，而dp[i]就应该对应的是最少的金币数
那么 f(x) 就是就是 x 金额时候，所处的状态
寻找状态方程
代码实现
var dp []int //定义动态数组
func coinChange(coins []int, amount int) int {
dp = make([]int, amount+1) //动态数组
for i := 1; i < len(dp); i++ { //f(0) = 0 的时候，是不需要金币的，这个可以想想那个树状图
dp[i] = 1000 //每一个都要设置一个较大的值
}
//要想抽出总金额i，至少需要 dp[i] 个金币
for i := 1; i <= amount; i++ {
dp[i] = Min(coins, i) + 1
}
if dp[amount] >= 1000 {
return -1
} else {
return dp[amount]
}
}
// 要凑够金额 amount，需要的最少的钱数
func Min(coins []int, amount int) int {
rel := []int{} //存储结果
for _, v := range coins {
if v > amount { //总钱数比货币最大值要大，就停止了。
rel = append(rel, 1000) //都已经退到头了，就说明，没有合适的金币了
break
} else {
// 比如总金额 10，可以由 5,8,9 这三种状态，经过一步到达，所以要看看他们几个里面最小的
s := dp[amount-v]
rel = append(rel, s)
}
}
// rel就是结果值，从结果值中取出最下的来
for i := 0; i < len(rel); i++ {
for j := i + 1; j < len(rel); j++ {
if rel[i] > rel[j] {
rel[i], rel[j] = rel[j], rel[i] //选出最小的值来
}
}
}
return rel[0]//取出结果最小的来。
}
如何把选择的顺序输出出来？
其实就是每次都把 l[i] = Min(coins, i) 这个里面的最小值找出来，就是那个两个 x 相减，就是差值
参考文献
[1]https://www.bilibili.com/video/BV1tp4y167c5?p=28&share_source=copy_web
