操作系统 の 内存管理
内存的使用
存在磁盘中的程序,转成汇编指令以后,用 call 40 ,表示调用位置为 40 地方的代码。但是程序的执行,是需要将程序加载到内存中实行的,那么此时的 call 要用到的地址,就必须是真实的物理地址,这个过程是如何实现的呢?
具体过程
-
先在内存中,找到一段空白的内存。
-
把程序加载到这一段内存中。
-
将这段内存的初试地址,记作基地址,然后把基地址编程真是的屋里地址,这一步叫做重定位。
重定位就是把内存中的相对地址,转换成实际地址。
在运行的时候重定位,也叫做地址翻译
一个程序一旦加载到内存中,那么他的地址就不会动了,,那么这个
基地址可以放在PCB中。但是进程在内存中,是支持换入换出的,在换入换出的过程中,所以,每次换入换出的时候,都要调换PCB中的基地址。
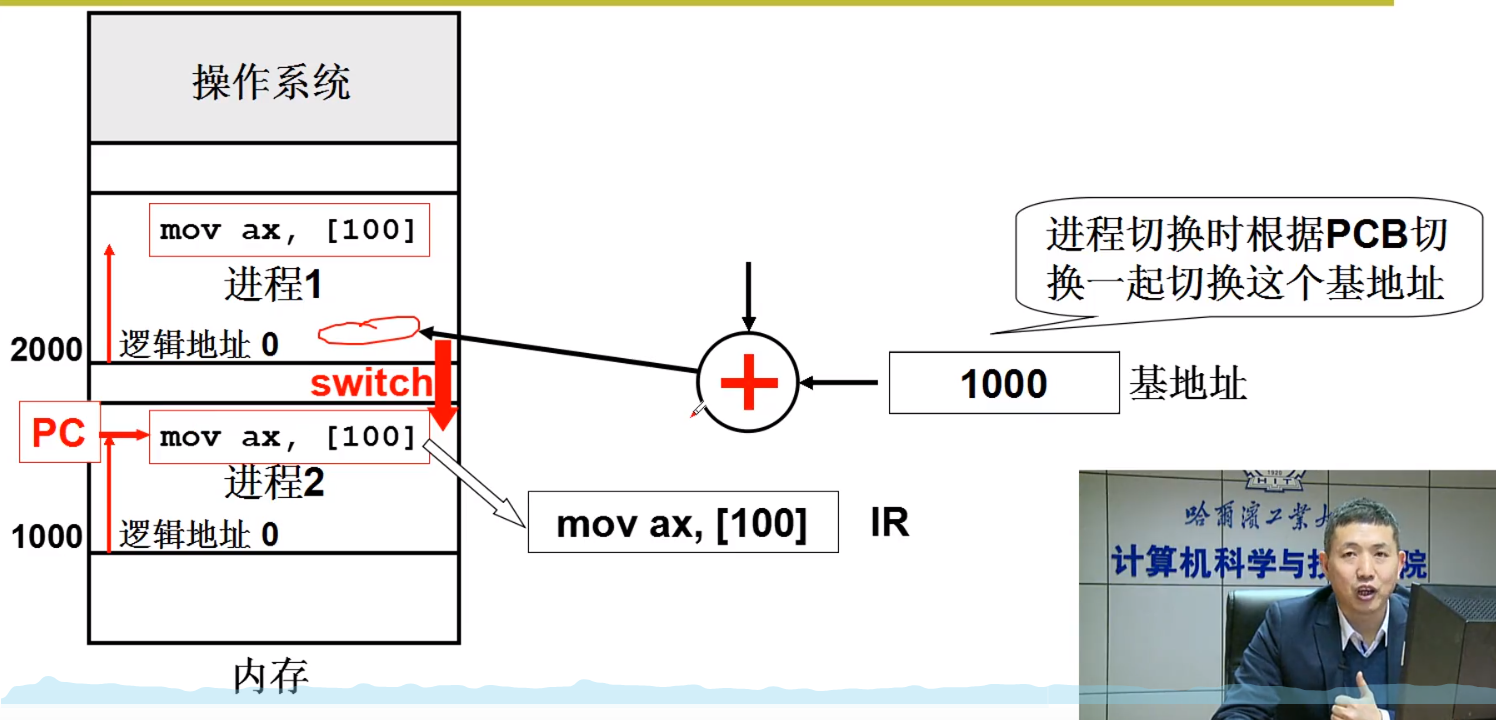
什么时候进行地址翻译呢?
一般如果是嵌入式系统,他的功能是固定的,每一次程序执行,都是使用固定的内存,那么可以在编译的时候进行翻译,但是大多数情况下,如PC机,因为内存资源比较珍贵,所以要经常把暂时用不到的进程,从内存挪到磁盘中去,用到的时候,再加载回来,这样的话,相当于程序对应的物理地址是要经常变化的,所以一般都是选择 在运行时候,进行地址翻译
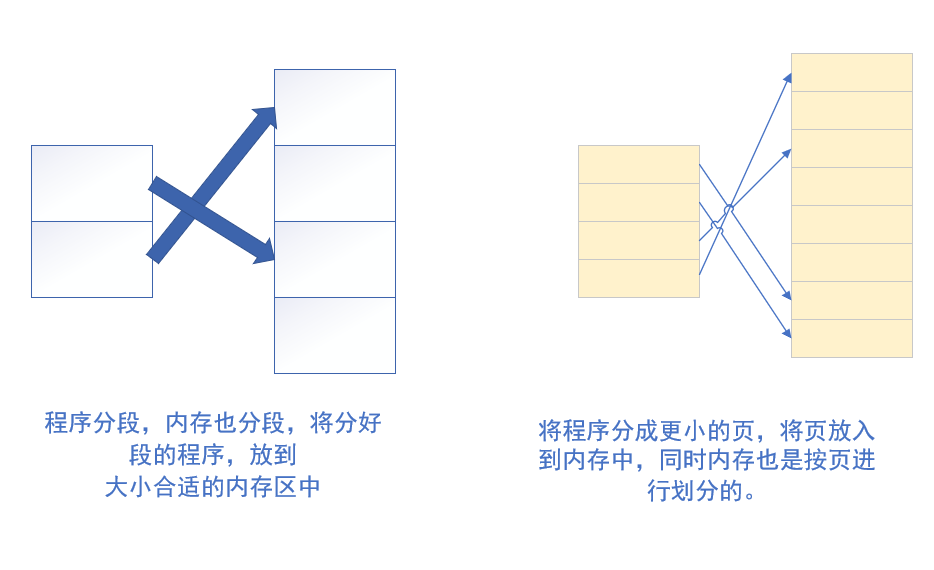
程序的分段
在实际的使用过程中,其实并不是将整个的程序,而是分段的放入到内存中。
程序分段是 编译过程 完成的。
为什么要分段?
这是因为代码的每一段,特点和用途其实是不一样的,比如代码段只读,而动态数组的部分是要动态增长的。比如说动态数组随着增长的过程中,内存不够了,就要把程序挪到一段更大的内存空间中去,如果要把整个的程序都要挪动,那么工作量就比较大了,如果只挪动态数组这一小段,就比较简单了,所以内存要分段。
分段了以后如何进行地址翻译?
如果程序分段了,那么就是相当于 堆、栈。是在内存中分开放的,那么此时应该如何定位到物理地址呢?就是使用段号 + 段内偏移
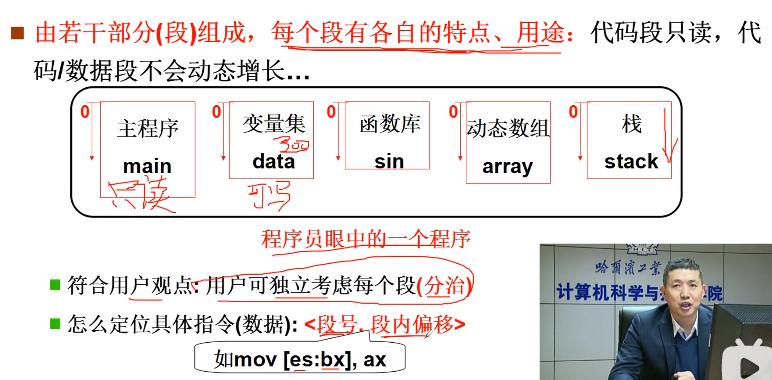
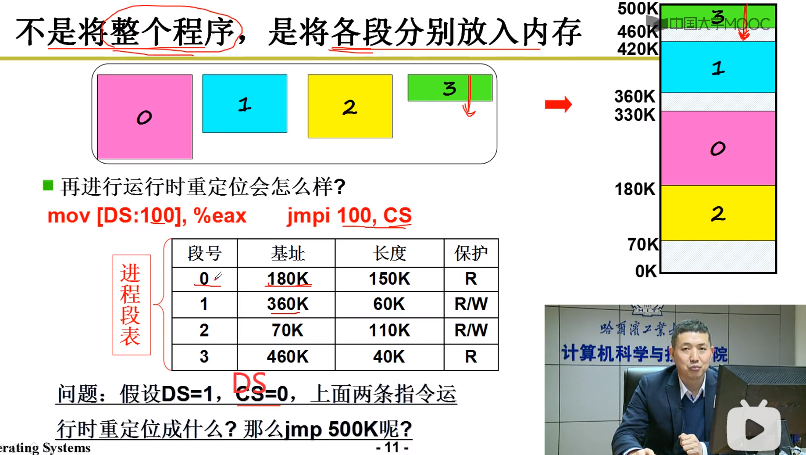
分段后的内存地址
分段以后,内存地址就要根据 <段号,段内偏移> 来进行地址翻译了。这就构成了 段表 (KDP)
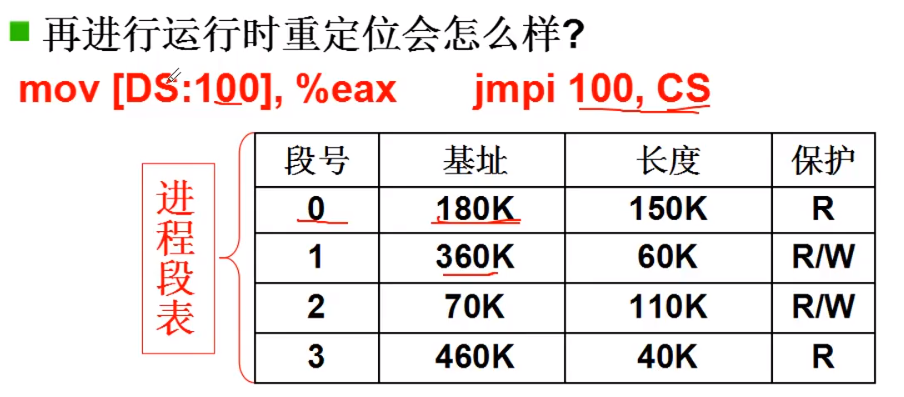
操作系统也可以看成是一个进程,他对应的段表,就叫做 GDT 表。
内存的分区与分页
之所以要引出分段和分度的话题,在于我们上边把程序的段,在内存中到一段空的内内存,放进去,问题在于,如何找?
分区
这些分区,一般来说大小是不相等的,有的是一直就是未分配的空内存,有的是原来有程序运行,但是现在运行完了,把内存释放出来了,这样的话,如何在这些内存中,找一个合适的 内存块,把程序放进去。
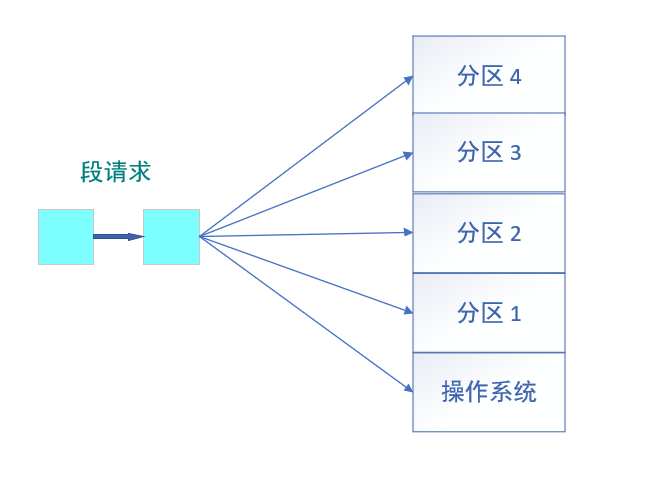
一般来说,有三种策略
- 首先适配:从上排着往下找,第一个找到的那个区。
- 最佳适配: 找到大小最合适的那个区
- 最差适配:每次都找内存最大的那个区
例题:
如果操作系统中,有的段很不规则,有时候需要很大的一个内存块,有时候又很小,此时使用那种分区分配算法?
A. 最先适配
B. 最佳适配
C. 最差适配
D. 没有区分
答案:最佳适配
这样分区存在的问题
这样存在的问题,即使因为分区的存在,会产生了很多的 内存碎片,导致了内存的利用率变低。
分页
为了解决内存采用 分区 造成的内存碎片过多,影响内存利用率低的问题,所以采用内存分页的方法。所以要采用分页的方法,即对内存中,每 4k 分成一个页。即最小的颗粒。这样的话,利用率就高了。同样的,这样如何进行查找呢?分区的时候,要通过 程序分段表,现在就要通过 程序分段表 进行地址翻译。
多级页表和快表
分页机制有他的好处,但是也有他的问题。
为了提高内存空间利用率,页应该小,但是页小了,页表就大了。关键是很多的页表,一般都是用不到的,他们在内存中,只是白白的占用空间。
所以解决方法是使用多级页表,有点类似于 B+ 树结构,只把最上一层的内容,放到多级页表中,其他的不放入。快表就是相当于,把经常使用的表加载到内存中。以方便日后快速使用。
段页结合的实际内存管理
虚拟内存
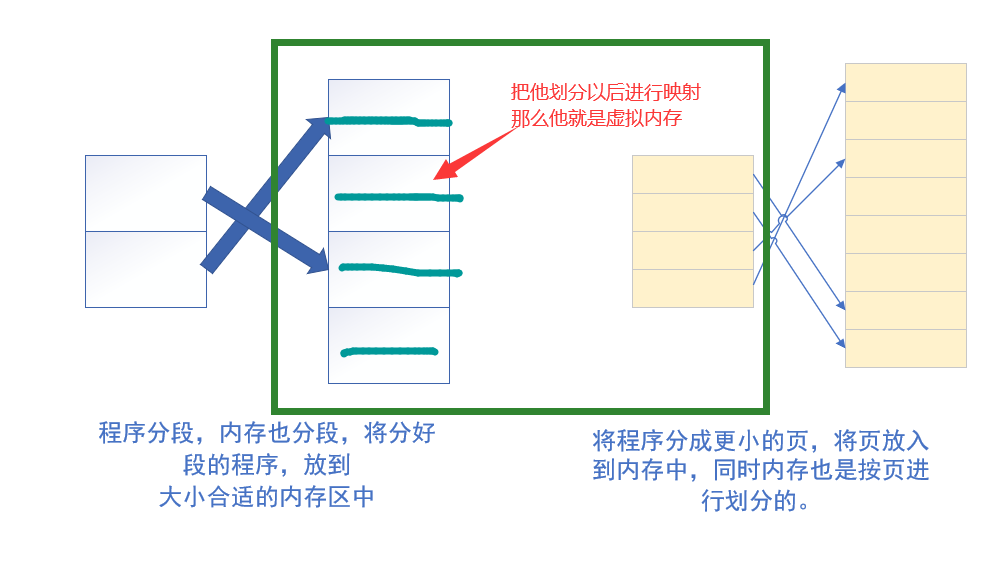
这样通过虚拟内存这个中间人,就可以将段映射到内存的页中,所以从用户的角度来看,他感觉是段,对于硬件来说 ,他操作的是页。中间的过程,用户是看不到的。对于用户是透明的。

内存的换入换出
分段和分页,是计算机内存管理的两大核心,而分段和分页的结合,就要依赖于 虚拟内存,虚拟内存技术能够实现,就要依赖于 内存的换入换出
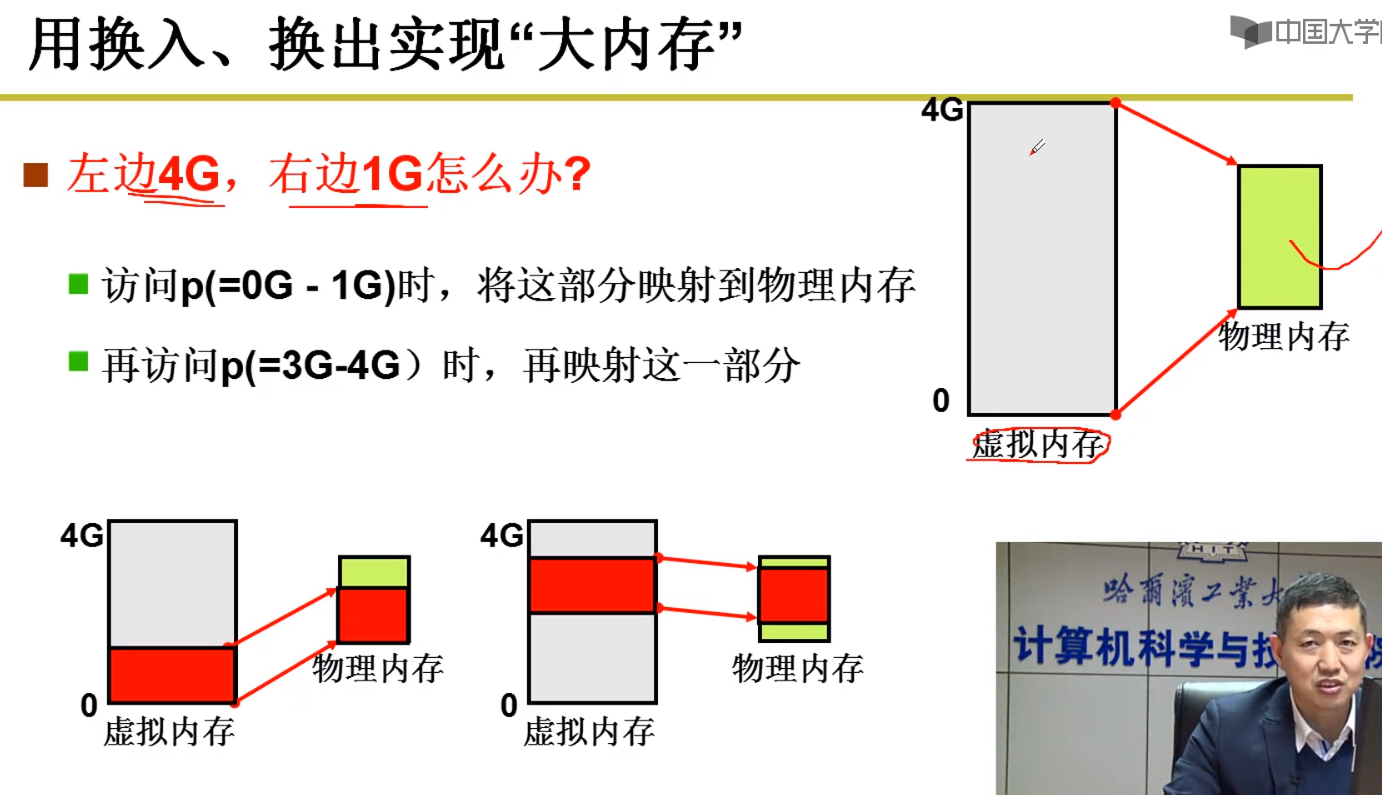
用户在编写程序的时候,实际的内存可能就 2G ,但是用户写程序的时候,会对应一个 4G 的虚拟内存,对于虚拟内存的空间,可以进行随意的分配。
当真正的要执行某一段程序的时候,从虚拟内存中取出这一段来,加载到物理内存中。要用到另一地址的时候,就把这一段再换出去,再从虚拟内存中,找到需要的那一段,加载到物理内存中
故事助记: 这就相当于是有一个商店,然后商店有个很大的仓库,他不可能把所有的东西,都拿到商店里,当有人买
A产品,就把A产品从仓库里找出来,放到商店的柜台上,如果有人买B商品,因为商店的柜台是有限的,所以他就会把A产品放回到仓库,再从仓库中取出B来,放到柜台上。
内存的换入(swap in)
当执行某一段的时候,从虚拟内存中取出这一段加载到物理内存中。
内存换出(swap out)
内存既然有换入,就应该有换出,其实这不部分的最大问题,在于选择选择哪一部分换出。其实这一部分的关键,就是 算法 。
淘汰算法
-
先入先出算法
-
MIN 方法
-
LRU
先入先出算法

看上图就可以看出这种方法的问题,刚把
A换出去,下一步又要把它换回来,这不是来回的折腾吗?
Min 最优算法
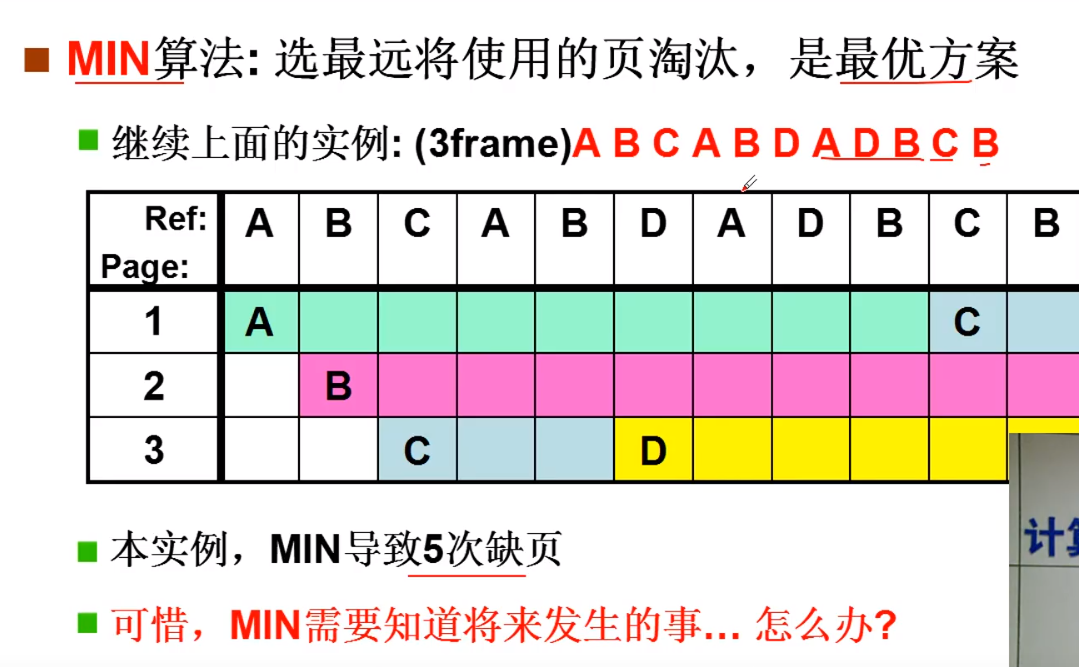
这种方案,就是要知道接下来要发生什么,然后在将来要发生的里面,把最后要调用的那个给换掉。
存在的问题: 他的问题,在于要知道将来发生的事情
LRU页面(最近最少使用)
因为最优算法,需要知道未来,所以我们可以从过去的历史中,预测将来。
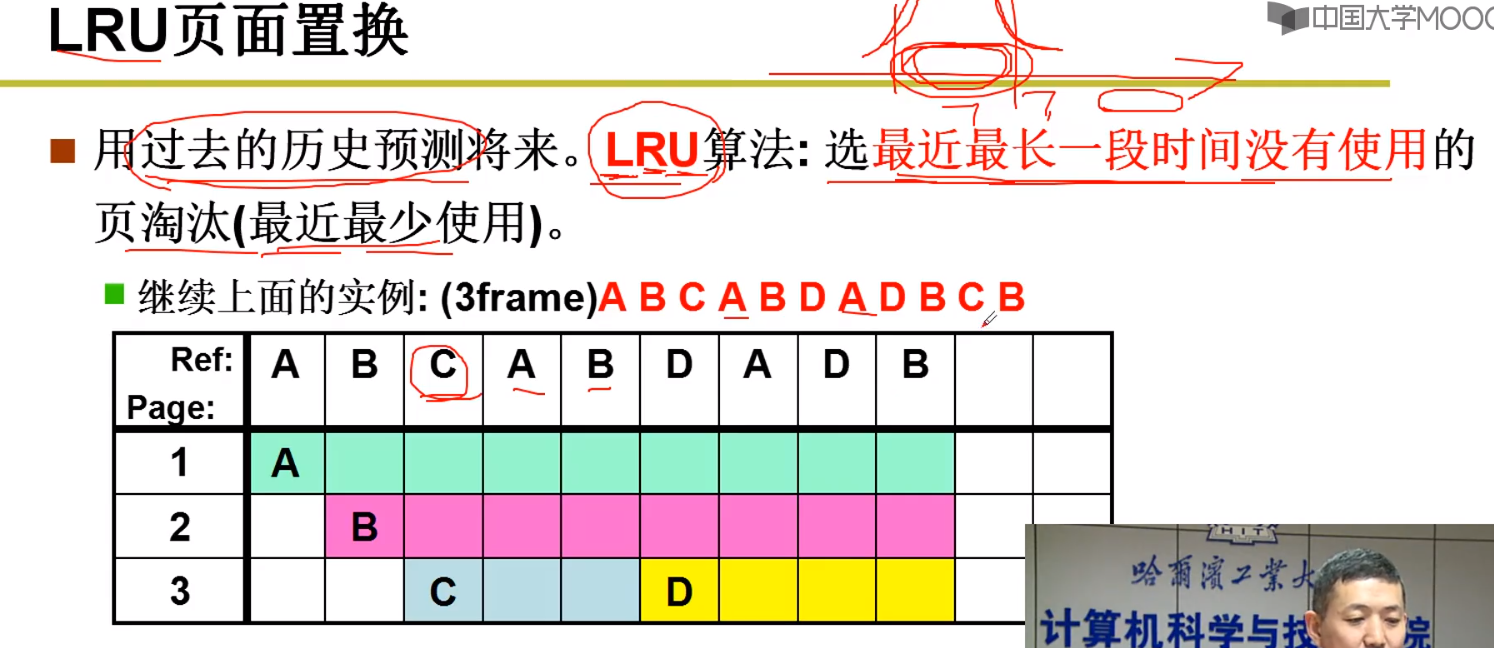
解释: 这种使用方法,之所以能够实现,是因为我们现实中的代码,都具有局部性,并不是随机的访问的,比如在 某个地方的for循环 他就可能频繁的访问这个程序。
使用栈的方法来实现 LRU
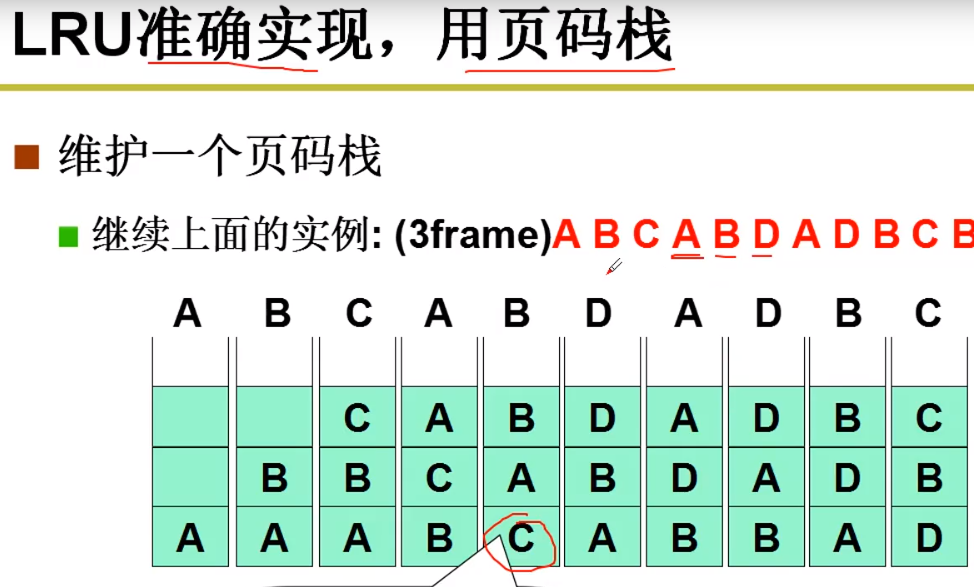
这样做的问题,就在于,每次我都要对栈进行调整和维护,性能消耗比较大。
LRU 的近似算法::二次机会算法
给每一页添加一个引用位,每访问一次,就要将改为置成 1,然后他会有一个指针进行扫描,当有扫描到该位的时候,就把 1 置成 0,遇到 0的话,就删除。
这种方法,为什么叫做近似的最近最少使用,因为这种方法,其实是去掉的最近没有使用,所以是近似
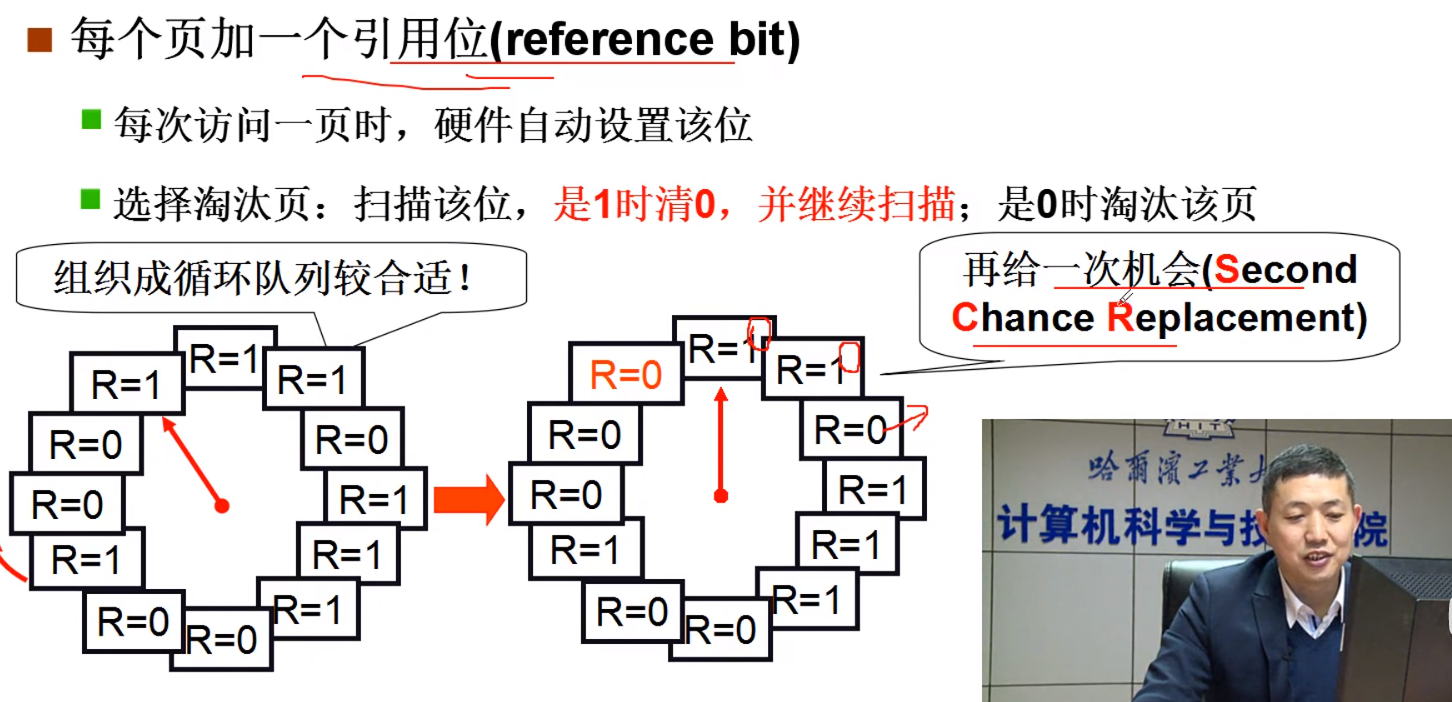
这种算法存在的问题:
一般缺页是很少出现的,因为程序具有局部性,如果你的程序老师缺页,那么说明你该增大你的内存条了。
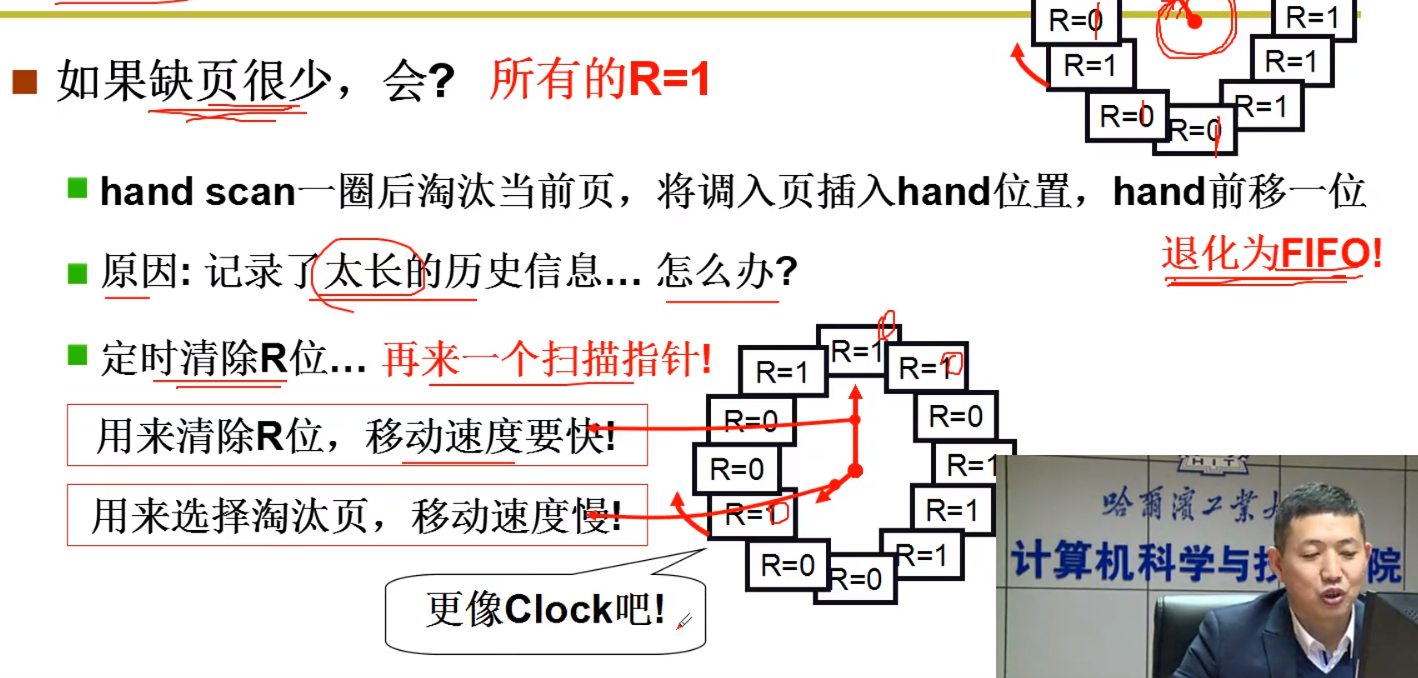
LRU 的近似算法::Clock算法
因为缺页是一般较少的,所以一般指针不动,这样的话,外边的数据不断访问,那么就导致最外边这一圈,全都是 1,那么此时再转动这个指针,就会把第第一个换出,第二次会第二个换出,那么这不就是又成了 先进先出算法 了吗?
出现这个情况的原因,就是因为你上面的那个指针,转的时间太长了,只能表示最少只用,而不能表示最近的含义。
如何解决这个问题呢?
那就是在这个里面,再加一个转的更快的指针(这个指针用可以用程序任意控制),用来清除 R 位,即把 R 的 1 置成 0,然后用转的慢的指针(在缺页的时候,就转这个指针),进行淘汰页。 这样就想一个 clock 了。
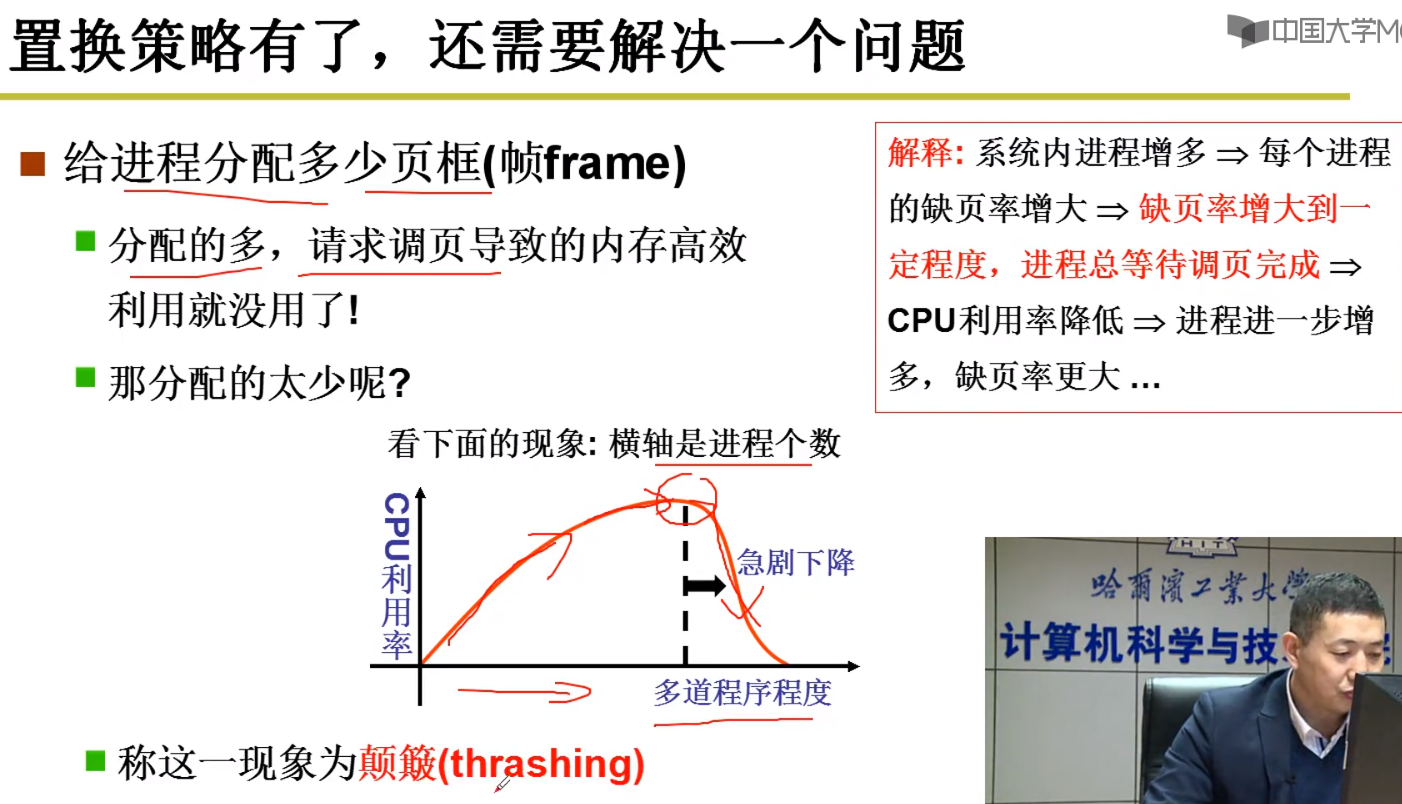
到底该给进程分配多少页呢?
- 分配多,就会导致请求掉页而让
CPU高效利用的优势就没有了。 - 但是太小的话,就会导致程序颠簸
参考文献
https://www.bilibili.com/video/BV1d4411v7u7?p=25&share_source=copy_web

 浙公网安备 33010602011771号
浙公网安备 33010602011771号