数据结构 の 图
图的基本该概念
边
为了将图和树做区分。往往将图中的节点，叫做顶点。两个定点中间存在边，则为相邻关系。
-
注意有向图的边称为
弧，分为弧头还有弧尾；无向图的边依旧称为边。 -
有向图还分
如度和出度
完全有向图和完全无向图
- 在有向图中，有n个顶点，那么最多有
n(n-1)条边，那么有 n(n-1) 条边的图叫做有向完全图 - 在无向图中，有n个顶点，那么最多有
n(n-1)/2条边，那么有n(n-1)/2条边的无向图就叫完全无向图
图的存储结构
图的存储其实有两种方式，一种是邻接表（链式存储），一种是邻接矩阵（顺序存储）
邻接矩阵表示法
type MGraph struct {
edges [][]int
n, e int // 分别表示定点数和边数
}
邻接表表示法
拓扑结构的优化（拓扑排序+深度优先遍历）
先认识几个英语单词
- Arc 弧
- Vertex 定点
- adjacent 邻接
type ArcNode struct {
adjvex int // 该边所指向的结点的位置
nextarc *ArcNode
info int //这个一般可以不写
}
type VNode struct {
data int //定点信息
firstarc *ArcNode //指向第一条边
}
type AGraphNode struct {
n, e int //定点和边的个数
adjlist []VNode // 邻接列表
}
深度优先算法
图的深度优先算法，有点类似于树的先序遍历，他的基本思想是，先访问任意一个出发点 V，将其标记为已访问，然后再遍历 'V' 的邻接节点中未访问过的任意一个W,并访问他。以此重复进行，当一个定点的所有邻接定点都被访问过了，就退回到最近被访问的节点，若节点中其他邻接节点中未被访问过的，则从这些未访问过的节点中选择一个进行访问。
package main
import "fmt"
type ArcNode struct { //邻接表
data int // 要指向的节点
nextNode *ArcNode // 下一个节点
}
type VNode struct {
data int //顶点
firstArcNode *ArcNode // 指向第一个节点
}
type AGraph struct {
vnodes []*VNode // 邻接表
vnumber int // 定点个数
arcNumber int //边的个数
}
var (
visit [20]int // 标记访问过的点
)
func NewGraph(v, arc int) AGraph { //创建一个新的表
agraph := new(AGraph)
agraph.vnumber = v // 节点的数目
agraph.arcNumber = arc // 边的数目
return *agraph
}
func DFS(aGraph *AGraph, i int) {
p := aGraph.vnodes[i].firstArcNode // 第一个定点
visit[i] = 1
fmt.Println("节点数", i) // 打印节点
p = p.nextNode // p指向下一个节点
for p != nil {
if visit[p.data] == 0 {
DFS(aGraph, p.data)
} else {
p = p.nextNode
}
}
}
func main() {
}
深度优先和广度优先算法
package main
import "fmt"
type ArcNode struct { // 根据图记忆
v_index int //定点指针
next *ArcNode
}
type VNode struct {
index int
firstArc *ArcNode
}
type AGraph struct {
n, e int // 表点
Vlist []VNode //直接使用即可，不要使用指针
}
func newAGraph(n int) *AGraph {
vList := make([]VNode, n)
for i := 0; i < len(vList); i++ {
vList[i].index = i
}
return &AGraph{
n: n,
e: 0,
Vlist: vList,
}
}
func addArc(G *AGraph, from, to int) {
G.e++ //变数+1
newarcNode := &ArcNode{
v_index: to,
}
if G.Vlist[from].firstArc == nil {
G.Vlist[from].firstArc = newarcNode
} else {
p := G.Vlist[from].firstArc
for p.next != nil {
p = p.next
}
p.next = newarcNode
}
}
var visitedDFS [10]int
func DFS(G *AGraph, v int) { // 深度优先遍历
visitedDFS[v] = 1 //标记为访问过了
fmt.Println("深度优先遍历输出：", v)
p := G.Vlist[v].firstArc
for p != nil {
if visitedDFS[p.v_index] == 0 {
DFS(G, p.v_index)
}
p = p.next
}
}
// 广度优先和树的层次遍历，都是不需要递归的
func BFS(G *AGraph) { // 广度优先遍历
var visited [20]int
var queue [20]int
front, rear := 0, 0
rear++
queue[rear] = 0
for front != rear {
front = (front + 1) % 20
j := queue[front] // 先出队
p := G.Vlist[j].firstArc // 循环的关注点，是定点的子节点，而不是节点本身
for p != nil {
if visited[p.v_index] == 0 {
fmt.Println("广度优先遍历输出", p.v_index)
visited[p.v_index] = 1
rear = (rear + 1) % 20
queue[rear] = p.v_index
}
p = p.next
}
}
}
func main() {
G := newAGraph(5)
addArc(G, 0, 1)
addArc(G, 0, 3)
addArc(G, 0, 4)
addArc(G, 1, 2)
addArc(G, 1, 4)
addArc(G, 2, 0)
addArc(G, 3, 2)
DFS(G, 0)
BFS(G)
}
例题应用
例一
设计一个算法，求无向连通图中，距离定点 v 最近的一个顶点
分析： 图的广度优先遍历，相当于树的层次遍历，那么最后访问的定点一定是距离定点最远的点。
拓扑排序
活动在顶点上的网(Activity On Vertex network AOV)是一种可以形象反应出来整个工程中，各个活动之间的先后关系的有向图。AOV 网是没有回路的，一旦出现回路，那么就表示一项活动以自己为前提，那么显然违背实际。
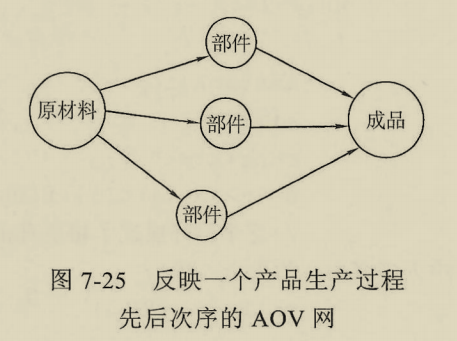
拓扑排序
对一个有向无环图进行拓扑排序，是将G中所有的定点排成一个线性序列，使图中任意两点 U,V，若存在 u 到 V 的路径，那么那么拓扑排序的时候，U 一定要到 V 的前边。
有向图中拓扑排序的步骤
- 在有向图中，选择一个入度为
0的定点输出 - 删除该定点，并删除从该顶点出发的边
- 重复上述两步，直到把 入度为
0的点全部删光
步骤
type VNode struct {
index int //定点的编号
in_count int //入度
firstArcNode *ArcNode //边
}
将各个定点的入度都存储在 in_count 中，另外设置一个栈，用来记录当前入度为 0的节点，还要设置一个计数器 n,用来记录已经输出的顶点个数。
算法开始的时候，将 n 置为 0 ，扫描所有的顶点，将入度为 0 的点入栈，然后在栈不为空的情况下，循环执行：出栈，将顶点输出，执行n++,并且将此顶点指向的定点的入度都-1,并将如度为 0 的顶点入栈，栈为空时，循环退出，循环退出后判断 n 是否等于定点的个数，相等拓扑排序成功，不想等，拓扑排序失败。
代码
func TopSort(Agraph *AGraph) bool {
var (
stak = Stack{ //定义栈
l: [20]int{},
top: -1,
}
n int //总数
)
// 将图中度为 0 的点入栈
for i := 0; i < len(Agraph.VList); i++ {
if Agraph.VList[i].in_count == 0 {
Agraph.VList[i].flag = 1
stak.top++
stak.l[stak.top] = i
}
}
for stak.top != -1 {
// 出栈
v_index := stak.l[stak.top]
stak.top--
n++
//将该栈所到顶点的入栈全部为-1
p := Agraph.VList[v_index].firstArcNode
for p != nil {
Agraph.VList[p.to].in_count--
p = p.next
}
// 将图中度为 0 的点入栈
for i := 0; i < len(Agraph.VList); i++ {
if Agraph.VList[i].in_count == 0 && Agraph.VList[i].flag == 0 {
Agraph.VList[i].flag = 1
stak.top++
stak.l[stak.top] = i
}
}
}
if n == len(Agraph.VList) {
return true
} else {
return false
}
}
结论
- 如果图
G中有环，那么图G就不能存在拓扑结构。 - 如果图
G中无环，那么图G的排序可能不止一种。
优化
就是使用 拓扑排序 + 深度优先算法
题目https://leetcode-cn.com/problems/course-schedule/
