数据结构 の 树
树的定义
由唯一的根和若干互不相交的子树,每一颗子树又是一棵树。
相关概念
- 结点的度:拥有子树的个数
- 树的度:树中各节点度的最大值
- 双亲节点:
- 祖先节点:他上边所有的节点都是祖先节点
- 森林:把树的根去掉,剩下的树就构成了森林
树的存储结构
树的存储有两种方式:顺序存储、链式存储
顺序存储:一般使用称双亲存储,一组数组就可以搞定
如知道了节点 i,那么 tree[i] 就是 i 的双亲节点

链式存储包括
孩子存储结构.
| 左孩子指针 | 数据 | 右孩子指针 |
|---|---|---|
| lchild | data | rchilid |
数据结构如下:
type BTNode struct {
data int
lchild *BTNode
rchilid *BTNode
}
孩子兄弟存储结构。
其实就是把右子树指向兄弟节点
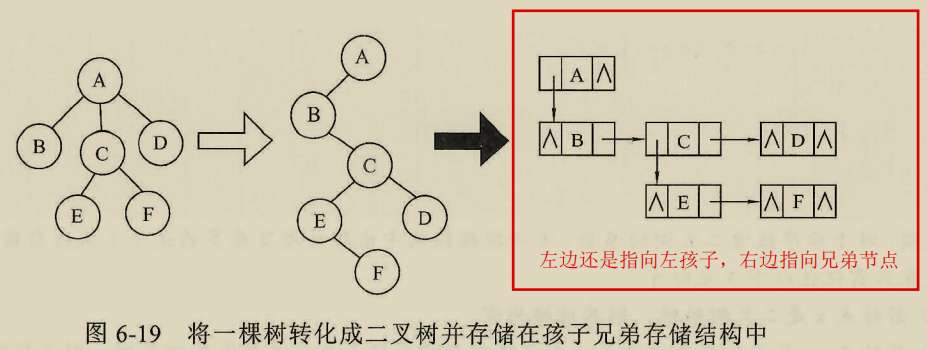
二叉树
在普通树上再加两个条件,就构成了完全二叉树。
- 每个节点最多有两个子树
- 子树有左右之分,不能颠倒
二叉树又分为满二叉树,完全二叉树,完全二叉树是由满二叉树由右到左,从下到上排着删得到的。不能跳着删除
二叉树主要性质
- 非空二叉树的叶子结点数,等于双分支结点数+1;
- 在二叉树的第 i 层上,最多有 2i-1个结点。
- 对于
k层深的树,最多有 2k -1 个节点
对于完全二叉树的第 i 结点来说:
-
i 的双亲节点为 【i/2】向下取整
-
如果
n>=2i那么i的左孩子的编号为2i,如果n<2i则无左结点 -
如果
n>=2i+1,则右节点为2i+1,如果n<2i+1则无右节点

二叉树的遍历
- 先序遍历
type treeNode struct {
data int
lchild *treeNode
rchild *treeNode
}
// 先序遍历
func preorder(treenode *treeNode) {
if treenode != nil {
Visit(treenode)
preorder(treenode.lchild)
preorder(treenode.rchild)
}
}

- 总序遍历
- 后序遍历
- 层次遍历
二叉树的层次遍历
func Level(node *BTNode) {
que := make([]*BTNode, 20) //20长的循环队列
front, rear := 0, 0 //初始化队列,当front=rear表示队为空
//rear+1=front 表示队列已经满了。
if node != nil {
rear = (rear + 1) % 20 // 根节点入队
que[rear] = node
for front != rear { // 如果不是空队
front = (front + 1) % 20
q := que[front] // 跟节点出队
Visit(q)
if q.lchilid != nil { // 如果有左节点就是入队
rear = (rear + 1) % 20
que[rear] = q.lchilid
}
if q.rchilid != nil { // 如果有右节点就入队
rear = (rear + 1) % 20
que[rear] = q.rchilid
}
}
}
}
常见问题
如何求一颗二叉树的深度
二叉树的深度,就是左右子树中,深度最大的,然后再加一; 所以步骤是,先求左子树,再求右子树,最后求 max{左,右}+1
求二叉树的公共祖先
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
if root == nil {
return nil
}
if root.Val == p.Val || root.Val == q.Val {
return root
}
//因为从二叉树到某一节点肯定就一条路径
left := lowestCommonAncestor(root.Left, p, q)
right := lowestCommonAncestor(root.Right, p, q)
// 如果左右节点,就从下往上送
if left != nil && right != nil {
return root
}
// 如果只有一个的话,就往上送一个
if left != nil {
return left
}
return right
}
森林还有树
森林还有树之间的转换,孩子兄弟链表的存储方式,具体还是看书吧。
赫夫曼树 (最小代价树)
赫夫曼树又叫最优二叉树,它的特点是带权路径最短。

赫夫曼树的构造过程

- 先从所有的节点中,找出两个权值最小的节点
- 将这两个节点构成一个新的树,然后,然后根节点权值就是左右之和
- 把这个节点放到之前的节点中去
- 以此类推着写
赫夫曼树的特点:
- 权值越大,和根节点的距离越近
- 树中没有度为 1 的节点,这类树叫做严格二叉树
- 树的带权路径长度最短
堆排序
堆是一种二叉树,只不过任何一个非叶子节点的值都不大于其左右孩子节点的值。若父亲大,孩子小,就叫大顶堆,若父亲小,孩子大,就叫小顶堆
根据堆的定义可知,堆的 根节点 的值是最大的,因此将一个无序的序列,调整为堆,就是要找到最大的,然后交换到序列的最前面,这样有序的关键字增加1,无序的关键字减少1,对新的无序序列重复这样的操作,就实现了排序。
代码
// 从 R[low]到R[high]的范围内对位置在low上的节点进行调整
// 没执行一直这个函数,就相当于位于 low 的这个点彻底调完,hight就是后来帮忙的。
func Sift(R []int, low, high int) {
i, j := low, 2*low // 树的节点,默认是从1开始的。
temp := R[i]
for j <= high {
if R[j] < R[j+1] && j < high { // 从左右节点中挑出来一个最大的
j++ // 变成右节点
}
if temp < R[j] {
R[i] = R[j] // 把j调整到双亲节点上
i = j // i是要放的节点 继续往下调整
j = i * 2
} else {
break
}
}
R[i] = temp // 把调整后的节点放在最终位置
}
func heapSort(R []int) {
// 调整顺序,先下后上,先右后左
n := len(R) - 1 // 因为序号要比次数-1,比如第5个节点,应该是 R[4]
for i := n / 2; i >= 1; i-- { // 叶子节点肯定都是堆,所以从 n/2 开始,应是从下到上,从右往左切换
Sift(R, i, n) // 循环调整完以后,最大的肯定在最上面。
}
for i := n; i >= 2; i-- {
R[1],R[i]=R[i],R[1]
Sift(R, 1, i-1) //把最大的和最后面的进行替换调整
}
}
func main() {
rand.Seed(time.Now().UnixNano())
r := make([]int, 20)
r[0] = 0
for i := 1; i < 20; i++ {
r[i] = rand.Intn(100)
}
fmt.Println(r)
heapSort(r)
fmt.Println(r)
}
二叉排序树
二叉排序树定义
- 若左子树不为
0,那么左子树上的所有关键字的值都不大于根关键字的值 - 若右子树不为
0,那么右子树上的所有关键字的值都不大小根关键字的值 - 左右子树又各是一棵二叉树
由二叉树的定义可以知道,如果输出二叉排序树的中序遍历,那么这个序列是非递减有序的。
平衡二叉树
平衡二叉函数是一种特殊的二叉排序树,其左右子树都是平衡二叉树,且左右子树的高度之差不超过 1 。
红黑树
从二叉树开始讲起,因为原本的 二叉搜索树 ,如果一直都是左子树,左子树,这样的结构,那么二叉搜索树就会退化成链表。
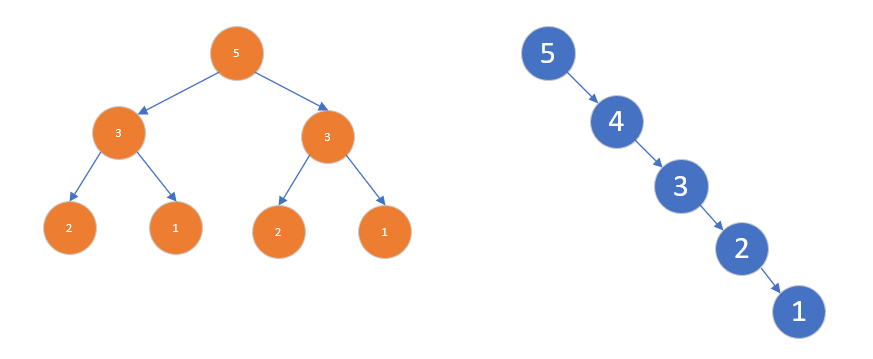
所以为此,提出了 二叉树,就是在原来二叉树的基础上,对左右子树的高度,进行了限定,就是左右高度差不能超过 1
但是正式因为 二叉排序树,这种特殊的结构,让我们在使用的过程中,需要对 二叉平衡树,进行不断的调整,因为 平衡二叉树 的要求,太苛刻了。因此发明了要求相对来说没有那么苛刻的 红黑树。
红黑树的特性
- 节点要么是红节点,要么是黑节点
- root 节点是黑节点
- 叶子节点或者
nil节点,也必须是黑节点(这也变相的保证了,一棵树,一半以上是黑节点) - 红节点的子节点,必须是黑节点
所以从上面苛刻的条件可以看出来,大多数的情况下,好像都是黑节点
- 新插入的节点为红色节点

 浙公网安备 33010602011771号
浙公网安备 33010602011771号