Python 入门基础—手写识别数字
1.Python基础
- Python 2.x 的时候,整数除整数是整数,但在 Python 3.x 的时候,整数除以整数是小数。
- 使用 type(10),可以查看数据类型。
- 数组的维数,可以使用 np.dim ( ) 获得,比如 3*2 的矩阵就是 2 维
列表: a=[1,2,3,4,5,6,7,8]
len(a)列表长度
a[4]是第四个元素的值
a[0:2] 是切片,获取索引为0到2的元素,但是不包括2
a[1: ] 获取索引为1到最后的元素
a[1:-1]获取从1到倒数第一个之前的元素
me = { “height” : 100 } 字典
me[“height”] 访问元素
2._init_方法,是构造函数,只在生成类实例的时候被调用一次,在生成类的时候会明确的写入表示类自身的 self 。(相当于类本身的构造函数)。详情见下边例子:
class Man:
def __init__(self,name):
self.name=name
print("Initialized")
def hellow(self):
print("Hellow---"+self.name+"!")
def goodbye(self):
print("Good-Bye"+self.name+"!")
m=Man("David")
m.hellow()
m.goodbye()
结果:
3. Numpy
- np.array() 方法,需要接受Python列表作为参数,生成 numpy.ndarray 数组,
-
能进行的操作: A= np.array ( [1,2],[3,4] )
A.shape---------结果是 (2,2)
A.dtype ---------结果是( int64 )
数组的维数,可以使用 np.dim ( ) 获得,比如 3*2 的矩阵就是 2 维
两个矩阵线程,使用 np.dot (A,B)。使用 dotnet 可以一次算出结果。
自动生成数组: x=np.arange ( 0, 6, 0.1 )
两个矩阵能 np.dot (A,B) 实现点乘的前提:
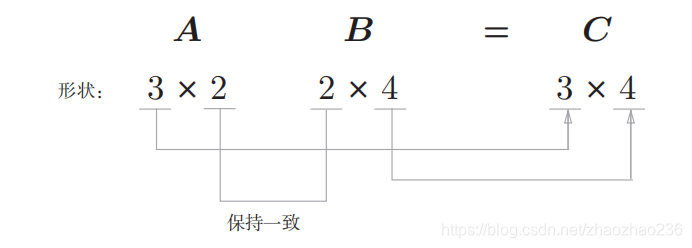
4.不同形状的数组之间也能进行运算,如 2*2 的矩阵 和标量10之间进行乘法运算,把10扩成2*2的矩阵了,这种功能叫做 “广播”
5.pyplot
import numpy as np
import matplotlib.pyplot as plt
x=np.arange(0,6,0.1) #以0.1为单位,生成0到6的数据
y1=np.sin(x) # x与y1 的函数关系
y2=np.cos(x)
plt.plot(x,y1,label="sin")
plt.plot(x,y2,label="cos",linestyle="--") # 用虚线描绘
plt.xlabel("x") # x标签
plt.ylabel("y") # y标签
plt.table("sin & cos")
plt.legend()
plt.show()
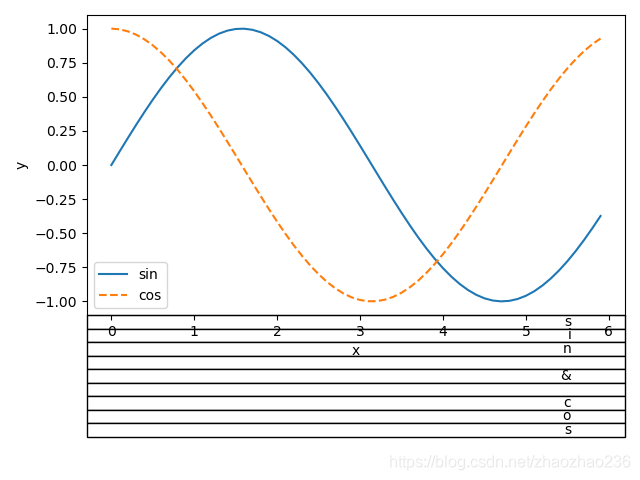
2. 感知机
1.下图为两个输入的感知机。
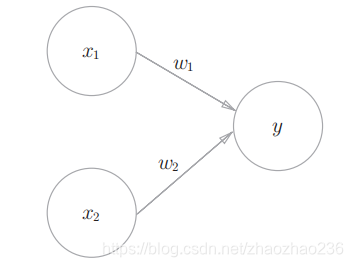
2.用数学公式表示出来
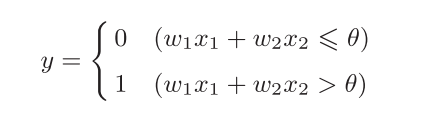
每个输入信号都有自己的权重,权重越大,对应的信号就越重要。
3.用 Python 来实现
import numpy as np
x=np.array([0,1]) #输入
w=np.array([0.5,0.5]) #权重
b=-0.7 #偏置
resule=np.sum(x*w)+b
print(resule)
结果:
-0.19999999999999996
4.线性非线性
如下图所示:曲线分割成的空间成为非线性空间,直线分割成的空间称为线性空间。
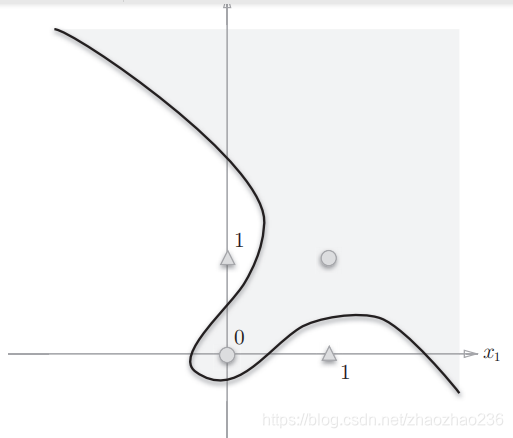
3.神经网络
- " 朴素感知机 " 是指的单层神经网络,使用了阶跃函数模型。
- “ 多层感知机 ” 指的是神经网络 ,即使用了 sigmoid 函数等 平滑的激活函数 的多层网络
1.激活函数:
- 感知机使用了阶跃函数
- 最近主要使用 ReLU 函数。大于 0 的时候,直接输出该值,小于0的时候,输出 0。
- 神经网络中经常的 sigmoid 函数
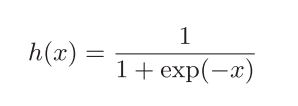
用Python来实现:
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x)) # 使用 np 的包求指数
x=np.array([-1,1.0,2.0])
result=sigmoid(x)
print(result)
结果:
[0.26894142 0.73105858 0.88079708]
sigmoid 函数的图形
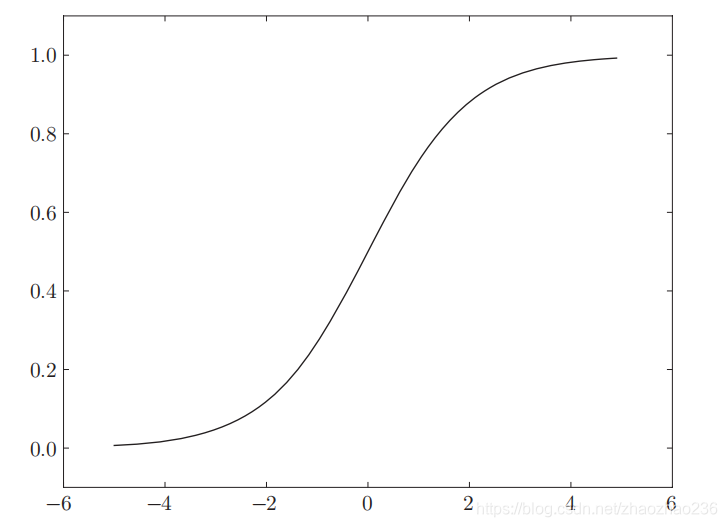
阶跃函数和 sigmoid 函数都是属于非线性函数,因为使用线性函数的话,加深神经网路就没有意义了
4.三层卷积神经网络
1.巧妙的使用 NumPy 数组,就可以用很少量的代码完成神经网络的前向处理。
2.看权重符号的含义:
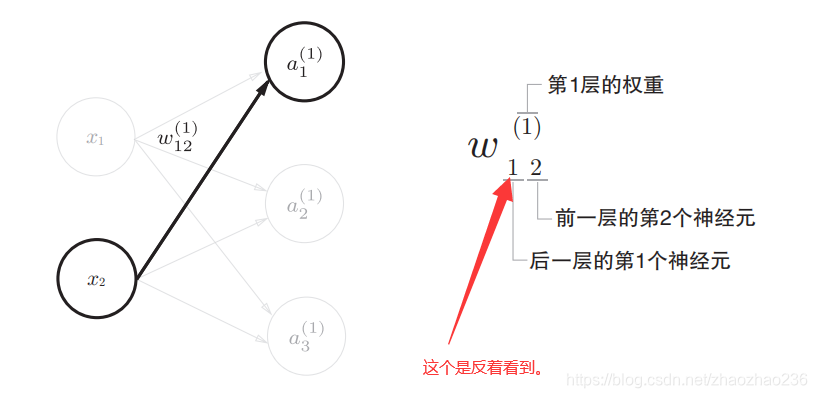
3.信号传递:
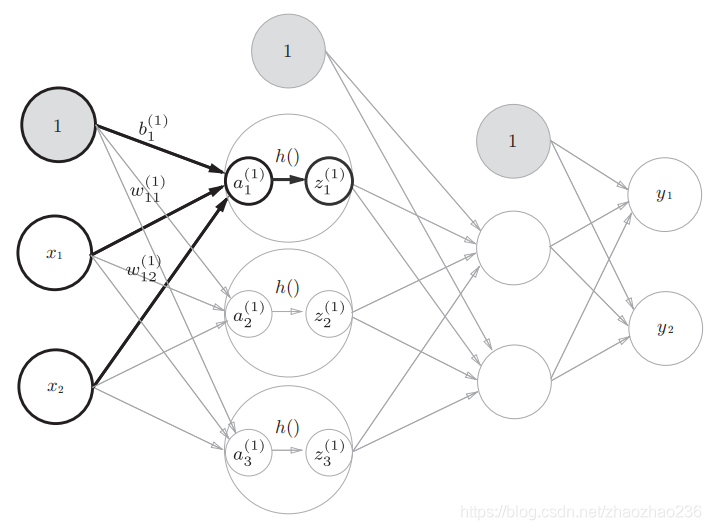
4.使用矩阵进行乘法运算非常简单,直接一个公式就可以出来:
理解下边的公式结构,首先脑子里要有图

用代码试下:
X=np.array([1.0,0.5])
W1=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1=np.array([0.1,0.2,0.3])
# 一层的加权公式
A1=np.dot(X,W1)+B1
Z1=sigmoid(A1)
同理第二层的代码:
A2=np.dot(Z1,W2)+B2
Z2=sigmoid(A2)
5.如果想让计算过程自动处理,可以使用 inti_network() 和 forward()函数。。 inti_network()会自动的进行权重和偏置的初始化。并将他们保存在字典变量 network 中,forward 则封装了相关的处理过程。其实也就是稍微简单了一点。
5.输出层的激活函数
注意,本小节所说的激活函数,都是属于输出层的激活函数。
- 回归问题用 恒等函数(预测连续值,比如一个人的体重变化)
- 二分类问题用 sigmoid 函数 (一个人是男人还是女人)
- 多元分类用 softmax 函数
softmax函数
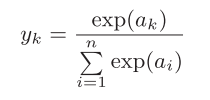
softmax函数的特性
- 输出的是 0.0 到 1.0 之间的实数
- 输出值的中和等于 1
- 我们一般把 softmax 函数的输出解释为概率
6.神经网络
神经网络的特征就是可以从数据中学习,所谓的从数据中学习,就是可以由数据自动的决定权重参数的值。像前边少的话,可以直接指定,在现实的网络中,数量可以成千上万,在更深的网络里面甚至上亿。
在机器学习中,将图像转化为向量所用的特征量仍是由人来设计的。而在神经网络中,连图像中包含重要特征量,也是由机器来学习的。
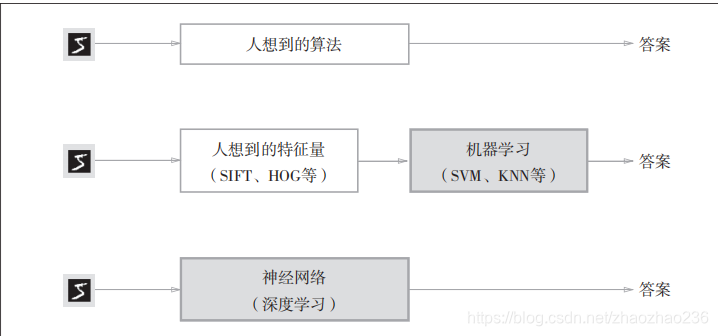
损失函数有很多种,最有名的是均方误差,除此之外还有交叉熵误差
mini-batch
如果要把所有的数据作为对象求损失函数的和,则计算需要花费较长的时间,神经网路学习可以从训练数据集中选择出一小批的数据(mini-batch)进行学习,作为全部数据的 “ 近似 ”,这种学习叫做 mini-batch 学习。
