2017.10.7 QBXT 模拟赛
T1
容斥原理,根据奇偶性进行加减

#include<iostream> #include<cstdio> using namespace std; typedef long long ll; typedef long double ld; #define rep(i,a,n) for(int i=a;i<=n;i++) ld eps=1e-9; ll pp=1000000007; ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} ll gcd(ll a,ll b){return (!b)?a:gcd(b,a%b);} ll read() { ll ans=0; char last=' ',ch=getchar(); while(ch<'0' || ch>'9')last=ch,ch=getchar(); while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); if(last=='-')ans=-ans; return ans; } void put(ll a) { if(a<0)putchar('-'),a=-a; int top=0,q[20]; while(a)q[++top]=a%10,a/=10; top=max(top,1); while(top--)putchar('0'+q[top+1]); } ll ans=0; int n,m,a[25]; ll Gcd(ll a,ll b) { if(!b)return a; return gcd(b,a%b); } void dfs(int dep,ll t,int flag) { if(t>n)return; if(dep==m+1) { ans+=n/t*flag; return; } dfs(dep+1,t,flag); dfs(dep+1,t/Gcd(t,a[dep])*a[dep],-flag); } int main() { n=read(); m=read(); rep(i,1,m)a[i]=read(); dfs(1,1,1); cout<<ans<<endl; return 0; }
T2
对于60%数据:我们需要对程序进行优化,枚举左端点的时候,要固定右端点。
可以再n^3内算出。根据插入排序,我们可以找出中位数找出
对于80%数据:一般求第k大,一般都是需要二分答案。我们二分中位数大于等于k有多少个,二分完中位数大于等于k个。
比如说:
A 1 2 3 4 5 k=3
B -1 -1 1 1 1
因为1,2是小于零,根君b数组进行判断有多少个大于等于k个。我们二分答案,再暴力一下,可以拿到80%
对于100%数据,我们要拿前缀和s[r]进行判断。我们要让s[r]-s[l-1]>0,我们要求逆序对,我们统计顺序对的个数,求逆序对是nlogn,总时间复杂度是nlognlogn

#include<algorithm> #include<iostream> #include<cstdio> using namespace std; typedef long long ll; typedef double ld; #define rep(i,a,n) for(int i=a;i<=n;i++) #define N 110000 ld eps=1e-9; ll pp=1000000007; ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} ll read() { ll ans=0; char last=' ',ch=getchar(); while(ch<'0' || ch>'9')last=ch,ch=getchar(); while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); if(last=='-')ans=-ans; return ans; } int a[N],b[N],c[N],d[N],e[N],n,m; ll k; int lowbit(int x){return x&(-x);} int bin(int k) { int l=1,r=m; while(l<r) { int mid=(l+r)/2; if(k<=d[mid])r=mid; else l=mid+1; } return l; } void add(int x) { for(;x<=m;x+=lowbit(x))e[x]++; } int find(int x) { int ans=0; for(;x;x-=lowbit(x))ans+=e[x]; return ans; } ll check(int k) { c[0]=0; rep(i,1,n)c[i]=c[i-1]+(a[i]>=k); rep(i,0,n)c[i]=c[i]*2-i,d[i+1]=c[i]; sort(d+1,d+n+2); d[0]=1; rep(i,2,n+1) if(d[i]!=d[d[0]])d[++d[0]]=d[i]; m=d[0]; ll ans=0; rep(i,0,n)c[i]=bin(c[i]); rep(i,0,m)e[i]=0; rep(i,0,n) if(i&1)add(c[i]); else ans+=find(c[i]-1); rep(i,0,m)e[i]=0; rep(i,0,n) if((i&1)==0)add(c[i]); else ans+=find(c[i]-1); return ans; } int main() { n=read();k=read(); rep(i,1,n)a[i]=read(),b[i]=a[i]; sort(b+1,b+n+1); b[0]=1; rep(i,2,n) if(b[i]!=b[b[0]])b[++b[0]]=b[i]; int l=1,r=b[0]; while(l<r) { int mid=(l+r)/2+1; ll tt=check(b[mid]); if(tt==k) { cout<<b[mid]<<endl; return 0; } if(check(b[mid])>k)l=mid; else r=mid-1; } cout<<b[l]<<endl; return 0; }
T3
对于60%数据,每一次排序只新增一个数字,我们可以进行插入排序,这样我们可以n^3做这道题。
对于80%数据:首先我们来考虑一下,一个区间是5,k=4,那么会被统计4次,这个数字被统计了多少次,说明有多少个数字小于他。一个数比他小,则会对这个数字多贡献一下
我们把t变一下,比如说还有t2,那么还有i2这一段比他小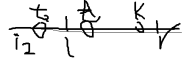
Sum=i+i2
Sum*(n-j+1)*k。所以我们只需要求出比k小的下标有多少个。
我们可以暴力做
对于100%数据:我们每一次找到比他小的下标进行维护,我们可以那树状数组,线段树甚至归并排序求出。我们先求出下标总和
比如:10 100 1000 à数据
1 2 3 à下标
这样我们可以那归并排序进行维护即可。

#include<algorithm> #include<iostream> #include<cstdio> #include<cmath> using namespace std; typedef long long ll; typedef double ld; typedef pair<int,int> pr; const double pi=acos(-1); #define rep(i,a,n) for(int i=a;i<=n;i++) #define pb push_back #define fi first #define sc second #define N 1001000 ld eps=1e-9; ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} ll read() { ll ans=0; char last=' ',ch=getchar(); while(ch<'0' || ch>'9')last=ch,ch=getchar(); while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); if(last=='-')ans=-ans; return ans; } pr a[N]; int c1[N],c2[N],n; ll pp=1000000007,A,B,C; int lowbit(int x){return x&(-x);} void add(int *c,int x,int w) { c[0]+=w; if(c[0]>=pp)c[0]-=pp; for(;x<=n;x+=lowbit(x)) { c[x]=c[x]+w; if(c[x]>=pp)c[x]-=pp; } } int find(int *c,int x) { int ans=0; for(;x;x-=lowbit(x)) { ans+=c[x]; if(ans>=pp)ans-=pp; } return ans; } int main() { cin>>n>>a[1].fi>>A>>B>>C; a[1].sc=1; rep(i,2,n) { a[i].sc=i; a[i].fi=(a[i-1].fi*A+B)%C; } sort(a+1,a+n+1); ll ans=0; rep(i,1,n) { int t1=find(c1,a[i].sc); int t2=c2[0]-find(c2,a[i].sc-1); t2=(t2+pp)%pp; int t3=(1ll*t1*(n-a[i].sc+1)+1ll*t2*a[i].sc)%pp; t3=(t3+1ll*a[i].sc*(n-a[i].sc+1))%pp; ans=(ans+1ll*t3*a[i].fi)%pp; add(c1,a[i].sc,a[i].sc); add(c2,a[i].sc,n-a[i].sc+1); } cout<<ans<<endl; return 0; }
我们都在命运之湖上荡舟划桨,波浪起伏着而我们无法逃脱孤航。但是假使我们迷失了方向,波浪将指引我们穿越另一天的曙光。


