洛谷 P1265 公路修建

题目描述

某国有n个城市，它们互相之间没有公路相通，因此交通十分不便。为解决这一“行路难”的问题，政府决定修建公路。修建公路的任务由各城市共同完成。

修建工程分若干轮完成。在每一轮中，每个城市选择一个与它最近的城市，申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。

政府审批的规则如下：

（1）如果两个或以上城市申请修建同一条公路，则让它们共同修建；

（2）如果三个或以上的城市申请修建的公路成环。如下图，A申请修建公路AB，B申请修建公路BC，C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请；

（3）其他情况的申请一律同意。

一轮修建结束后，可能会有若干城市可以通过公路直接或间接相连。这些可以互相：连通的城市即组成“城市联盟”。在下一轮修建中，每个“城市联盟”将被看作一个城市，发挥一个城市的作用。

当所有城市被组合成一个“城市联盟”时，修建工程也就完成了。

你的任务是根据城市的分布和前面讲到的规则，计算出将要修建的公路总长度。

输入输出格式

输入格式：

 

第一行一个整数n，表示城市的数量。(n≤5000)

以下n行，每行两个整数x和y，表示一个城市的坐标。(-1000000≤x，y≤1000000)

 

输出格式：

 

一个实数，四舍五入保留两位小数，表示公路总长。（保证有惟一解）

 

输入输出样例

输入样例#1：

4
0 0
1 2
-1 2
0 4

输出样例#1：

6.47

说明

修建的公路如图所示：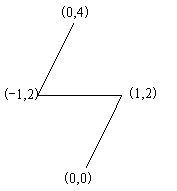

 

 

裸prim算法

屠龙宝刀点击就送

#include <cstdio>
#include <cmath>
#define N 5055
typedef long long LL;
int n;
LL x[N],y[N],f[N];
double dis[N];
bool vis[N];
double calc(LL x1,LL y1,LL x2,LL y2) {return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));}
double prim(int s)
{
    for(int i=0;i<=n;++i) dis[i]=1e18,vis[i]=0;
    vis[s]=1;
    for(int i=1;i<=n;++i) dis[i]=calc(x[s],y[s],x[i],y[i]);
    double ans=0;
    for(int i=2;i<=n;++i)
    {
        int t=0;
        for(int j=1;j<=n;++j) if(!vis[j]&&(t==0||dis[t]>dis[j])) t=j;
        if(t)
        {
            vis[t]=1;
            ans+=dis[t];
            for(int j=1;j<=n;++j)
            if(j!=t&&!vis[j])
            {
                 double l=calc(x[t],y[t],x[j],y[j]);
                 if(l<dis[j]) dis[j]=l;
            }
        }
    }
    return ans;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;++i) scanf("%lld%lld",&x[i],&y[i]);
    printf("%.2lf",prim(1));
    return 0;
}