高斯核函数

 

 

 

高斯核函数

高斯核函数（Gaussian kernel），

也称径向基 (RBF) 函数，是常用的一种核函数。

它可以将有限维数据映射到高维空间，我们来看一下高斯核函数的定义：

 

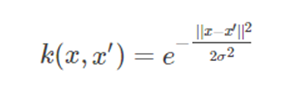
上述公式涉及到两个向量的欧式距离（2范数）计算，

而且，高斯核函数是两个向量欧式距离的单调函数。

σ 是带宽，控制径向作用范围，

换句话说，σ 控制高斯核函数的局部作用范围。

一维情况

 

 

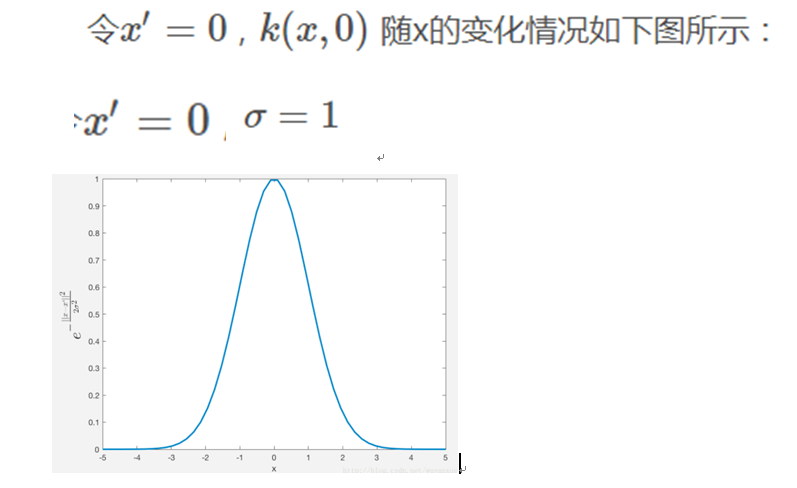
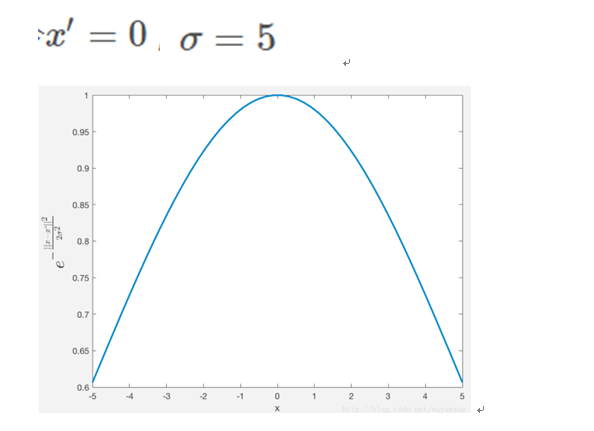
我们看到，随着x 与x′的距离的距离的增大，其高斯核函数值在单调递减。并且，σ越大，那么高斯核函数的局部影响范围就会越大。

 

 

 

 

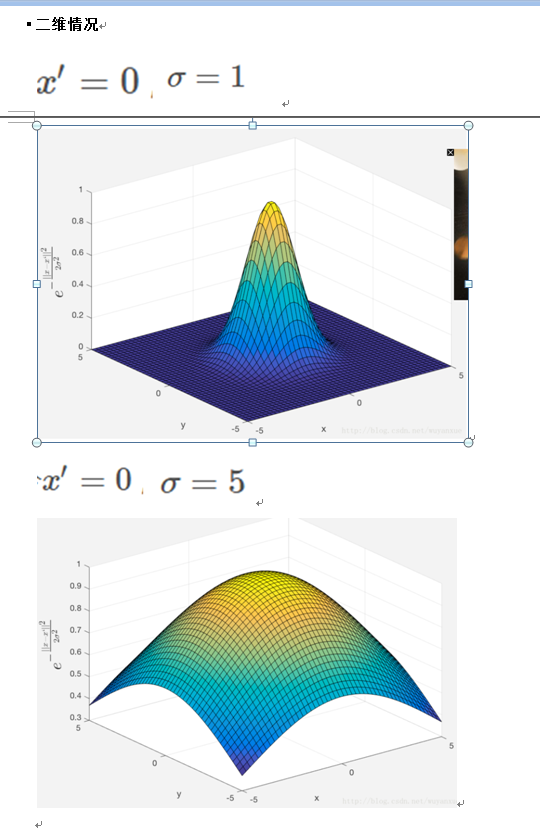
径向对称

圆形的对称，如圆和椭圆分别以直径和长短轴对称

欧氏距离

欧几里得度量（euclidean metric）（也称欧氏距离）是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。