网易机试
一、


1、
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int Inte[100000];
int SlpOrCle[100000];
int SlpOrCle1[100000];
int SumInte1(int *a,int *b,int n) //求兴趣点;
{
int suminte1=0;
for(int i=0;i<n;i++)
{
if(b[i]==1)
suminte1+=a[i];
}
return suminte1;
}
int main()
{
int n,k;
while(cin>>n>>k) //输入第一行
{
int Maxinte=0;
for(int i=0;i<n;i++)
cin>>Inte[i]; //输入第二行
for(int i=0;i<n;i++)
cin>>SlpOrCle[i]; //输入第三行
for(int i=0;i<n;i++)
SlpOrCle1[i]=SlpOrCle[i]; //复制数据。
vector<int> Zeros; //存放0的位置
for(int i=0;i<n;i++)
{
if(SlpOrCle[i]==0)
Zeros.push_back(i);
}
for(int i=0;i<Zeros.size();i++)
{
for(int j=Zeros[i];j<(Zeros[i]+k) and j<n;j++)
{
SlpOrCle1[j]=1; //叫醒后,置1
}
int a;
a=SumInte1(Inte,SlpOrCle1,n); //调用函数,n为课堂分钟
if(a>Maxinte)
{
Maxinte=a; //找最大的
}
for(int i=0;i<n;i++)
SlpOrCle1[i]=SlpOrCle[i]; //归为原始数据
}
cout<<Maxinte;
}
return 0;
} //6 3 1 3 5 2 5 4 1 1 0 1 0 0
通过率50% ,运行超时。
思路其实是,循环搜索所有的0位置,置为1,每次需要把所有的值重新计算一遍,当数据量大时,就会超时。
2、
每次叫醒后,都会新增一部分兴趣值,所以只需要找出最大的新增的兴趣值就可。然后加上本来就醒着的兴趣值。
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int Inte[100000];
int SlpOrCle[100000];
int SlpOrCle1[100000];
int main()
{
int n,k;
while(cin>>n>>k) //输入第一行
{
int Maxinte=0;
for(int i=0;i<n;i++)
cin>>Inte[i]; //输入第二行 ,兴趣值
for(int i=0;i<n;i++)
cin>>SlpOrCle[i]; //输入第三行,清醒or瞌睡
vector<int> Zeros; //存放0的位置
for(int i=0;i<n;i++)
{
if(SlpOrCle[i]==0)
Zeros.push_back(i);
}
int OriInte=0;
for(int i=0;i<n;i++)
{
if(SlpOrCle[i]==1)
{
OriInte+=Inte[i]; //最初的兴趣值
}
}
int MaxAddInte=0;
for(int i=0;i<Zeros.size();i++)
{
int InteTem=0;
for(int j=Zeros[i];j<(Zeros[i]+k) and j<n;j++) //每个叫醒点,后面的k个值,新增的兴趣值,找出最大
{
if(SlpOrCle[j]==0)
{
InteTem+=Inte[j]; //增加的兴趣值
}
}
if(MaxAddInte<InteTem)
MaxAddInte=InteTem; //找出最大的新增的兴趣值
}
Maxinte=OriInte+MaxAddInte;
cout<<Maxinte;
}
return 0;
} //6 3 1 3 5 2 5 4 1 1 0 1 0 0
通过 90%。
上面代码优化了不用每次都计算所有的兴趣值,转化为 固定的兴趣值+新增的最大兴趣值
找最大兴趣值是依次搜索0的位置,其后的k个值中,睡着的兴趣值相加。当K很大时,依旧会造成重复计算。
3、k个数据依次右移的方法来找最大的新增兴趣值。
#include<iostream>
#include<vector>
using namespace std;
int Inte[100000];
int SlpOrCle[100000];
int SlpOrCle1[100000];
int MaxAddInte(int *a,int *b,int n,int k)
{
int maxInte=0;
int temInte=0;
for(int i=0;i<k;i++) //得到第一个k组数中0对应的兴趣和
{
if(b[i]==0)
{
temInte+=a[i];
}
}
maxInte=temInte;
for(int i=k;i<n;i++) //k组右移
{
if(b[i]==0) //右移一位,判断加的位置为0,兴趣值加
{
temInte+=a[i];
}
if(b[i-k]==0) //右移一位,判断最左边少的位置为0,则减
{
temInte-=a[i-k];
}
if(temInte>maxInte) //右移一位后,判断最大新增值
maxInte=temInte;
}
return maxInte;
}
int main()
{
int n,k;
while(cin>>n>>k) //输入第一行
{
int Maxinte=0;
for(int i=0;i<n;i++)
cin>>Inte[i]; //输入第二行 ,兴趣值
for(int i=0;i<n;i++)
cin>>SlpOrCle[i]; //输入第三行,清醒or瞌睡
vector<int> Zeros; //存放0的位置
int OriInte=0;
for(int i=0;i<n;i++)
{
if(SlpOrCle[i]==0)
Zeros.push_back(i);
else
OriInte+=Inte[i]; //最初的兴趣值
}
int AddInte;
AddInte=MaxAddInte(Inte,SlpOrCle,n,k);
Maxinte=OriInte+AddInte;
cout<<Maxinte;
}
return 0;
} //6 3 1 3 5 2 5 4 1 1 0 1 0 0
测例全部通过。
二、


1、先求和再查找的过程
#include <iostream>
using namespace std;
int ap[100000];
int qu[100000];
int Quiry(int *a,int b,int n) //查询在第几堆
{
if(b<a[0])
return 1;
int i=0;
while(a[i]<b and a[i+1]<b) //从小到大查询
{
i++;
}
return i+2;
}
int main()
{
int n,m;
while(cin>>n)
{
int tem=0;
for(int i=0;i<n;i++)
{
int num;
cin>>num;
tem=tem+num;
ap[i]=tem; //苹果个数累和
}
cin>>m;
for(int i=0;i<m;i++)
{
cin>>qu[i]; //查询的数量
}
for(int i=0;i<m;i++)
{
cout<<Quiry(ap,qu[i],n)<<" ";
}
}
return 0;
} //5 2 7 3 4 9 3 1 25 11

从小到大的查询,时间复杂度太大。
2、
#include <iostream>
#include<math.h>
using namespace std;
int ap[100000];
int qu[100000];
int Quiry(int *a,int b,int n) //二分法查询
{
if(b<a[0])
return 1; //特殊情况
int imin=0,imax=n;
while((imax-imin)>1)
{
if( b>a[(int)ceil((imin+imax)/2)] )
imin=(int)ceil((imin+imax)/2);
else
imax=(int)ceil((imin+imax)/2);
}
return imax+1;
}
int main()
{
int n,m;
while(cin>>n)
{
int tem=0;
for(int i=0;i<n;i++)
{
int num;
cin>>num;
tem=tem+num;
ap[i]=tem; //苹果个数累和
}
cin>>m;
for(int i=0;i<m;i++)
{
cin>>qu[i]; //查询的数量
}
for(int i=0;i<m;i++)
{
cout<<Quiry(ap,qu[i],n)<<endl;
}
}
return 0;
} //5 2 7 3 4 9 3 1 25 11
通过所有用例。
3、利用c++ stl
一个数组number序列为:4,10,11,30,69,70,96,100.设要插入数字3,9,111.pos为要插入的位置的下标
则
pos = lower_bound( number, number + 8, 3) - number,pos = 0.即number数组的下标为0的位置。
pos = lower_bound( number, number + 8, 9) - number, pos = 1,即number数组的下标为1的位置(即10所在的位置)。
pos = lower_bound( number, number + 8, 111) - number, pos = 8,即number数组的下标为8的位置(但下标上限为7,所以返回最后一个元素的下一个元素)。
所以,要记住:函数lower_bound()在first和last中的前闭后开区间进行二分查找,返回大于或等于val的第一个元素位置。如果所有元素都小于val,则返回last的位置,且last的位置是越界的!!~
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
int n,m,t;
ll a[100005];
ll q;
int main()
{
cin>>n;
a[0]=0;
for(int i=1;i<=n;i++){
cin>>t;
a[i]=a[i-1]+t; //苹果累和
}
cin>>m;
for(int i=0;i<m;i++){
cin>>q;
int loc=lower_bound(a+1,a+n+1,q)-a; //利用stl 来查找位置
cout<<loc<<endl;
}
return 0;
}
4、
#include <iostream>
#include<math.h>
using namespace std;
int ap[100000];
int qu[100000];
int main()
{
int n,m;
while(cin>>n)
{
int tem=0;
for(int i=1;i<=n;i++)
{
int num;
cin>>num;
tem=tem+num;
for(int j=tem-num+1;j<=tem;j++)
{
ap[j]=i;
cout<<ap[j]<<" ";
}
cout<<endl;
}
for(int j=1;j<=25;j++)
{
cout<<ap[j]<<" ";
}
cin>>m;
for(int i=0;i<m;i++)
{
cin>>qu[i]; //查询的数量
}
for(int i=0;i<m;i++)
{
cout<<ap[qu[i]]<<endl;
}
}
return 0;
} //5 2 7 3 4 9 3 1 25 11

思路是生成一个向量,将所有的苹果的堆数存入该向量。第i个苹果的堆数为ap[i]。
但通过率30%。


可以看到测试用例很大,所以将所有苹果都生成向量,计算量过大,不会完全通过。
三、


#include <iostream>
#include <vector>
using namespace std;
int main()
{
int a,b,c;
while(cin>>a>>b>>c)
{
int Max;
Max=a+b+c;
if(Max<(a*b*c))
Max=a*b*c;
if(Max<((a+b)*c))
Max=(a+b)*c;
if(Max<((a+c)*b))
Max=(a+c)*b;
if(Max<((c+b)*a))
Max=(c+b)*a;
cout<<Max;
}
return 0;
}
所有公式计算下,找最大的就可以了。
题很简单,没难度。
四、

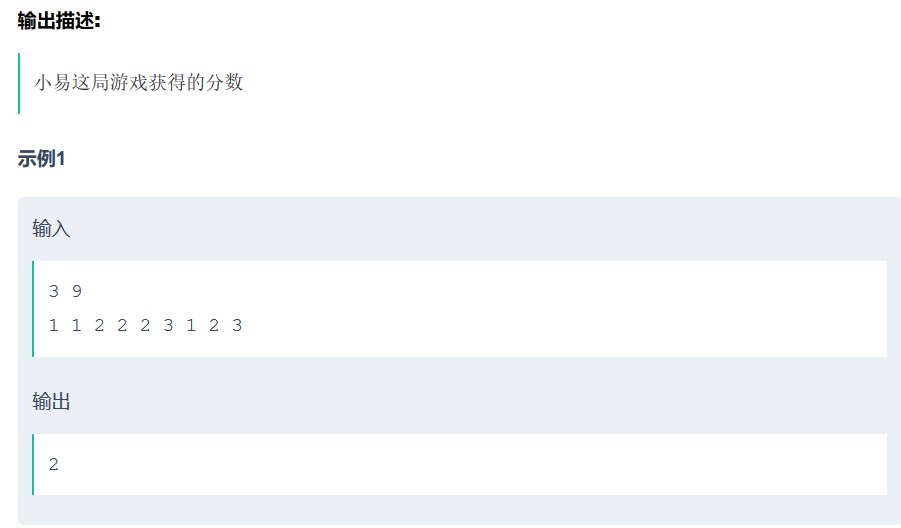
相当于统计1、2、3的个数,找出最小的个数值,就为应得的分数。
#include<iostream>
using namespace std;
int main()
{
int m=0,n=0,mid;
cin>>n>>m;
int a[100000]={0,0};
for(int i=0;i<m;i++)
{
cin>>mid;
a[mid]++;
}
mid =m+1;
for(int i=1;i<=n;i++)
{
if(mid>a[i])
mid =a[i];
// cout<<a[i]<<' ';
}
cout<<mid<<endl;
return 0;
}



