算法(一)
动态规划
一、递归

#include<iostream>
#include<string>
using namespace std;
int n;
int Hanoi(int n)
{
if(n==1)
{
return 1;
}
else
{
return 2*Hanoi(n-1)+1;
}
}
int main()
{
int n=3;
cout<<Hanoi(n);
}
2、递推
#include<iostream>
#include<string>
using namespace std;
const int Max=64;
int h[Max]={0};
int main()
{
int n;
cin>>n;
h[1]=1;
for(int i=2;i<=n;i++)
{
h[i]=h[i-1]*2+1;
}
cout<<h[n]<<endl;
}

二、


1、二维数组的定义
#include<iostream>
#include<algorithm>
#define Max 101
using namespace std;
int D[Max][Max];
int n;
//int MaxSum(int i,int j)
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
for(int j=0;j<=i;j++)
cin>>D[i][j];
}
for(int i=0;i<n;i++)
{
for(int j=0;j<=i;j++)
cout<<D[i][j]<<" ";
cout<<endl;
}
}
2、
#include<iostream>
#include<algorithm>
#define Max 101
using namespace std;
int D[Max][Max];//输入初始矩阵图
int n;//全局变量
int s=0;
int MaxSum(int i,int j)//i,j 到底部的最大距离
{
if(i==n)//边界条件,到底部时,等于本身
{
return D[i][j];
}
else
{
return D[i][j]+max(MaxSum(i+1,j),MaxSum(i+1,j+1));//返回位置到底部的最大距离,自己值,加上次求解的最大值。
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
cin>>D[i][j];
}
cout<<endl;
cout<<MaxSum(1,1);
//5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
}
因为是三角形,所有情况就都会通过递归搜索得到。
3、


#include<iostream>
#include<algorithm>
#define MAX 101
using namespace std;
int D[MAX][MAX];//输入初始矩阵图
int n;//全局变量
int s=0;
int maxSum[MAX][MAX];
int MaxSum(int i,int j) //i,j位置的数到最底层的最大距离
{
if(maxSum[i][j]!=-1)
return maxSum[i][j];
else
{
if(i==n)//到最底层时,距离就是本身
{
maxSum[i][j]=D[i][j];
}
else
{
maxSum[i][j]=D[i][j]+max(MaxSum(i+1,j),MaxSum(i+1,j+1));
}
return maxSum[i][j];
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>D[i][j];
maxSum[i][j]=-1;
}
}
cout<<endl;
MaxSum(1,1);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cout<<maxSum[i][j]<<" ";
}
cout<<endl;
}
//cout<<MaxSum(1,1);
// cout<<s;
//5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
}
将各个位置的距离记录下来,省去一次次的迭代。可以极大效率的提高运行速度,注意这里不能每次只存最大量,需要保存所有的值。
4、看到上面记录表,可以考虑将递归改为递推,不用重复迭代那么多次。
#include<iostream>
#include<algorithm>
#define MAX 101
using namespace std;
int D[MAX][MAX];//输入初始矩阵图
int n;//全局变量
int maxSum[MAX][MAX];
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>D[i][j];
}
}
for(int i=1;i<=n;i++)
{
maxSum[n][i]=D[n][i];//最后一行赋值
}
for(int i=n-1;i>=1;i--)
{
for(int j=1;j<=i;j++)
maxSum[i][j]=D[i][j]+max(D[i+1][j],D[i+1][j+1]);//
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cout<<maxSum[i][j]<<" ";
}
cout<<endl;
}
//cout<<MaxSum(1,1);
// cout<<s;
//5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
}
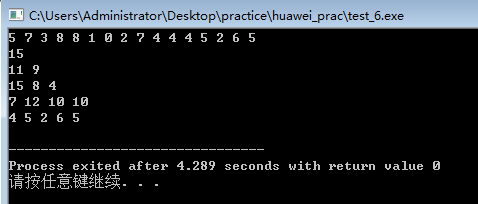
出错的原因是混淆了递推加的是变化后的值,而不是初始值。
#include<iostream>
#include<algorithm>
#define MAX 101
using namespace std;
int D[MAX][MAX];//输入初始矩阵图
int n;//全局变量
int maxSum[MAX][MAX];
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>D[i][j];
}
}
for(int i=1;i<=n;i++)
{
maxSum[n][i]=D[n][i];//最后一行赋值
}
for(int i=n-1;i>=1;i--)
{
for(int j=1;j<=i;j++)
maxSum[i][j]=D[i][j]+max(maxSum[i+1][j],maxSum[i+1][j+1]);//比较的是新的数组
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cout<<maxSum[i][j]<<" ";
}
cout<<endl;
}
//cout<<MaxSum(1,1);
// cout<<s;
//5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
}
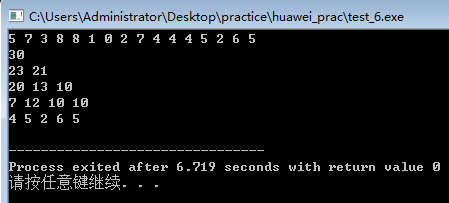
5、空间优化
#include<iostream>
#include<algorithm>
#define MAX 101
using namespace std;
int D[MAX][MAX];//输入初始矩阵图
int n;//全局变量
int *maxSum;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
cin>>D[i][j];
}
}
maxSum=D[n];//指向第n行
for(int i=n-1;i>=1;i--)
{
for(int j=1;j<=i;j++)
maxSum[j]=D[i][j]+max(maxSum[j],maxSum[j+1]);//比较的是新的数组
}
for(int i=1;i<=n;i++)
cout<<maxSum[i]<<" ";
//cout<<MaxSum(1,1);
// cout<<s;
//5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
}
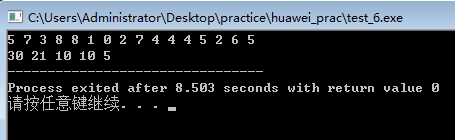
三、


1、错误实例
#include<iostream>//错误实例
#include<algorithm>
using namespace std;
const int Maxn=1010;
int a[Maxn];
int maxLen[Maxn];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
maxLen[i]=1;
}
for(int i=2;i<=n;i++)
{
for(int j=1;j<=i-1;j++)
{
if(i=2&&a[j]<=a[i])
{
maxLen[i]++;
break;
}
else if(a[j]<=a[i]&&a[j]>a[j-1])
{
maxLen[i]++;
}
}
cout<<maxLen[i]<<" ";
}
cout<<endl;
int Max=maxLen[1];
for(int i=1;i<=n;i++)
{
if(maxLen[i]>Max)
Max=maxLen[i];
}
cout<<Max;
//7 1 7 3 5 9 4 8
}
上面这段程序是错误的,错误的根源是没有理解清楚该如何递推,只是单纯的比较,并没有归纳到将前一次的比较运用到这次来。
2、
#include<iostream>
#include<algorithm>
using namespace std;
const int Maxn=1010;
int a[Maxn];
int maxLen[Maxn];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
maxLen[i]=1;
}
for(int i=2;i<=n;i++)
{
for(int j=1;j<=i-1;j++)
{
if(a[i]>=a[j])
maxLen[i]=max(maxLen[i],maxLen[j]+1);//从小于i的数每个都比较,如果大于,说明上升子序列可以加1,最后比较多组,找出最大的
}
cout<<maxLen[i]<<" ";
}
cout<<endl;
int Max=maxLen[1];
for(int i=1;i<=n;i++)
{
if(maxLen[i]>Max)
Max=maxLen[i];
}
cout<<Max;
//7 1 7 3 5 9 4 8
}
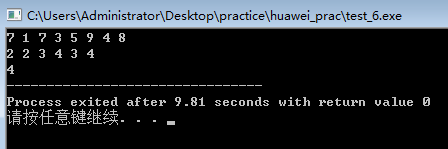
#include<iostream>
#include<algorithm>
using namespace std;
const int Maxn=1010;
int a[Maxn];
int maxLen[Maxn];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
maxLen[i]=1;
}
for(int i=2;i<=n;i++)
{
for(int j=1;j<=i-1;j++)
{
if(a[i]>=a[j])
maxLen[i]=max(maxLen[i],maxLen[j]+1);
}
cout<<maxLen[i]<<" ";
}
cout<<endl;
cout<<*max_element(maxLen+1,maxLen+n+1);//新的找最大值的方法
//7 1 7 3 5 9 4 8
}
3、最大最小值
#include<iostream>
#include<algorithm>
using namespace std;
bool cmp(int a,int b)
{
return a<b;
}
int main()
{
int num[]={2,3,1,6,4,5};
cout<<"最小值是 "<<*min_element(num,num+6)<<endl;
cout<<"最大值是 "<<*max_element(num,num+6)<<endl;
cout<<"最小值是 "<<*min_element(num,num+6,cmp)<<endl;
cout<<"最大值是 "<<*max_element(num,num+6,cmp)<<endl;
return 0;
}
 s、
s、
四、


#include<iostream>
#include<cstring>
using namespace std;
const int Max=64;
char sz1[1000],sz2[1000];
int maxLen[1000][1000];
int main()
{
while(cin>>sz1>>sz2)
{
int l1=strlen(sz1);
int l2=strlen(sz2);
int ntmp;
for(int i=0;i<=l1;i++)//边界条件,0代表空串
maxLen[i][0]=0;
for(int j=0;j<=l2;j++)
maxLen[0][j]=0;
for(int i=1;i<=l1;i++)
{
for(int j=1;j<=l2;j++)
{
if(sz1[i-1]==sz2[j-1])
maxLen[i][j]=maxLen[i-1][j-1]+1;//i,j 都加1
else
maxLen[i][j]=max(maxLen[i][j-1],maxLen[i-1][j]);
}
}
for(int i=0;i<=l1;i++)
{
for(int j=0;j<=l2;j++)
{
cout<<maxLen[i][j]<<" ";
}
cout<<endl;
}
cout<<maxLen[l1][l2]<<endl;
}
// abcfbc abfcab
}
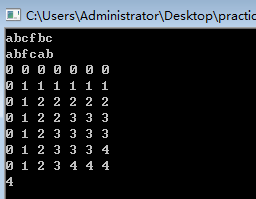
0的存在是边界,整个矩阵可以看出并不是对称矩阵,所以else的判断条件尤为重要。
五、

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=1000;
const int inf=0x3f3f3f3f;
int n;
char c[maxn];
int dp[maxn][maxn];
int num[maxn][maxn];
int m;
int NUM(int x,int y) //从x位置到y位置的数
{
if(num[x][y]!=-1)
{
return num[x][y];
}
int sum=0;
for(int i=x;i<y;i++)
{
sum=sum*10+c[i]-'0';
}
num[x][y]=sum;
return sum;
}
int DP(int p,int x) //p个字符,x个加号;
{
if(dp[p][x]!=-1) //一开始是等于-1;不等于-1说明计算过了
{
return dp[p][x];
}
if(x==0) //没有加号
{
dp[p][0]=NUM(0,p); //字符串变数字
return dp[p][0];
}
dp[p][x]=inf;
for(int k=p-1;k>=x;k--)//k会发生变化,控制加号可能出现的位置。大于x是为了给加号留够位置。
{
dp[p][x]=min(dp[p][x],DP(k,x-1)+NUM(k,p));//dp在多次循环比较中找到最小的 !循环递归化
}
return dp[p][x];
}
int main()
{
while(cin>>c)//输入字符
{
memset(dp,-1,sizeof(dp)); //全部赋为-1;
memset(num,-1,sizeof(num));
scanf("%d",&m); //输入加号个数
n=strlen(c);
printf("%d\n",DP(n,m)); //n个字符,m个加号
}
return 0;
}
#include<iostream>
#include<string>
#include<cstring>
using namespace std;
const int Max=100;
const int N=20;
const int inf=0x3f3f3f3f;
int mindit[Max][N];//存放Max个字符,N个加号 ,最小值
int n;
int L;
string str;
int Num(int x,int y)//k位置到L位置
{
int sum=0;
for(int i=x;i<y;i++)
{
sum=sum*10+str[i]-'0';
}
return sum;
}
int MinDit(int P,int x)
{
if(mindit[P][x]!=-1)
return mindit[P][x];
else if(x==0)//边界条件的核心
{
return Num(0,P);
}
else
{
mindit[P][x]=inf;
for(int k=P-1;k>=x;k--)
{
mindit[P][x]=min(mindit[P][x],MinDit(k,x-1)+Num(k,P));
}
return mindit[P][x];
}
}
int main()
{
getline(cin,str);//数字符串
cin>>n;//加号个数
memset(mindit,-1,sizeof(mindit));//二维数组赋值同样值方式
L=str.length();
cout<<MinDit(L,n)<<endl;
}
换用string 和去掉和的求解空间。
六、

1、递归

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
//递归方法,求解最长回文子序列
int lps(char *str, int i, int j) //字符串i和j之间的回文字符长度
{
if (i == j)
return 1; //只有一个元素,回文长度为1
if (i > j)
return 0; //因为只计算序列str[i....j]
//如果首尾相同
if (str[i] == str[j])
return lps(str, i + 1, j - 1) + 2;
//如果首尾不同
else
return max(lps(str, i, j - 1), lps(str, i + 1, j));
}
int main()
{
char str[] = "cabbeaf";
int n = strlen(str);
int res = lps(str, 0, n-1);
cout << res<< endl;
return 0;
}
2、

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int Maxn=100;
int Len[Maxn][Maxn];
//递归方法,求解最长回文子序列 ,自下而上
int lps(char *str, int n) //字符串i和j之间的回文字符长度
{
memset(Len,0,sizeof(Len));//赋值 Len[i][j]是i和j位置处的回文长度
int temp;
for(int i=0;i<n;i++)
{
Len[i][i]=1;//1个长度
}
for(int i=1;i<n;i++)
{
for(int j=0;j+i<n;j++)
{
if(str[j+i]==str[j])
{
Len[j][j+i]=Len[j+1][j+i-1]+2;//初设值为0,才对
}
else
{
Len[j][j+i]=max(Len[j+1][j+i],Len[j][j+i-1]);
}
}
}
return Len[0][n-1];
}
int main()
{
char str[] = "cabbeaf";
int n = strlen(str);
int res = lps(str,n);
cout << res<< endl;
return 0;
}
动态规划的思想就是用矩阵记录迭代的值,不用重复迭代,关键是如何循环给矩阵赋值。该题就是从小到大的间距给矩阵赋值,使得下次的赋值能用上次的赋值。
3、求解回文数的个数
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 50 + 5;
LL dp[maxn][maxn];
char s[maxn];
int main()
{
scanf("%s", s + 1);
int len = strlen(s + 1);
memset (dp, 0, sizeof(dp));//初值为0;
for(int i = 1; i <= len; i++)
{
for(int l = 1; l + i - 1 <= len; l++)
{
int r = l + i - 1;//dp[1][1],dp[2][2],dp[3][3]
//dp[1][2],dp[2][3]
dp[l][r] += dp[l + 1][r];
dp[l][r] += dp[l][r - 1];
if (s[l] == s[r])
dp[l][r] += 1;
else
dp[l][r] -= dp[l + 1][r - 1];
}
}
printf ("%lld\n", dp[1][len]);
return 0;
}




