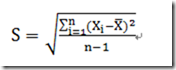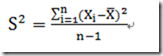数学公式
一、泰勒公式
数学中,泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数足够平滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还给出了这个多项式和实际的函数值之间的偏差。

用一点及其各阶导数表示整体。
常用泰勒展开

欧拉公式

最美公式

二、统计学的基本概念
(1)均值、方差、标准差
统计学里最基本的概念就是样本的均值、方差、标准差。首先,我们给定一个含有n个样本的集合,下面给出这些概念的公式描述:
均值描述的是样本集合的中间点,它告诉我们的信息是有限的,而标准差给我们描述的是样本集合的各个样本点到均值的距离之平均。
以这两个集合为例,[0, 8, 12, 20]和[8, 9, 11, 12],两个集合的均值都是10,但显然两个集合的差别是很大的,计算两者的标准差,前者是8.3后者是1.8,显然后者较为集中,故其标准差小一些,标准差描述的就是这种“散布度”。之所以除以n-1而不是n,是因为这样能使我们以较小的样本集更好地
x=[0 8 12 20];
y=[8 9 11 12];
E_x=mean(x);
E_y=mean(y);
subplot(211),plot(x,'*-')
hold on
subplot(211),plot(y,'o-')
grid on
xlabel('n');ylabel('x/y');
title('x、y原始数据')
legend('x','y')
V_x=var(x);
V_y=var(y);
subplot(212),plot(E_x,'*')
hold on
subplot(212),plot(E_y,'o')
hold on
subplot(212),plot(V_x,'*-')
hold on
subplot(212),plot(V_y,'o-')
grid on
xlabel('n');ylabel('x/y');
title('x、y均值与方差')
legend('x均值','y均值','x方差','y方差')
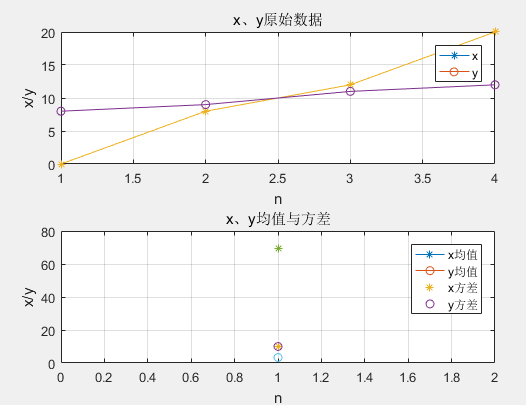
(2)协方差
标准差和方差一般是用来描述一维数据的,但现实生活中我们常常会遇到含有多维数据的数据集,最简单的是大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集,我们当然可以按照每一维独立的计算其方差,但是通常我们还想了解更多,比如,一个男孩子的猥琐程度跟他受女孩子的欢迎程度是否存在一些联系。协方差就是这样一种用来度量两个随机变量关系的统计量,我们可以仿照方差的定义:
来度量各个维度偏离其均值的程度,协方差可以这样来定义:
协方差的结果有什么意义呢?如果结果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义),也就是说一个人越猥琐越受女孩欢迎。如果结果为负值, 就说明两者是负相关,越猥琐女孩子越讨厌。如果为0,则两者之间没有关系,猥琐不猥琐和女孩子喜不喜欢之间没有关联,就是统计上说的“相互独立”。
从协方差的定义上我们也可以看出一些显而易见的性质,如:
(3)协方差矩阵


注意这里的维数是指的几个变量,而不是每个变量中的数据个数。
clear all %% %生成数据,列是维度,行是样本 data=randi([10,50],10,3); data_1=data(:,1);%维度 data_2=data(:,2); data_3=data(:,3); %% C_data=cov(data)%利用MATLAB自带方差公式计算的协方差矩阵 %% %计算对角线的协方差值,也就是维度自己和自己的方差 C_1_1=sum((data_1-mean(data_1)).^2)/(length(data_1)-1) C_2_2=sum((data_2-mean(data_2)).^2)/(length(data_2)-1) C_3_3=sum((data_3-mean(data_3)).^2)/(length(data_3)-1) %维度与纬度之间的方差 C_1_2=sum((data_1-mean(data_1)).*(data_2-mean(data_2)))/(length(data_1)-1) C_1_3=sum((data_1-mean(data_1)).*(data_3-mean(data_3)))/(length(data_1)-1) C_3_2=sum((data_3-mean(data_3)).*(data_2-mean(data_2)))/(length(data_3)-1)
 初始数据
初始数据
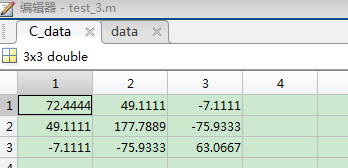 方差数据
方差数据
 自己计算数据。
自己计算数据。
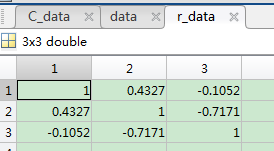
(4)相关系数

%求相关系数 r_data=corrcoef(data)%系统函数求 %对角线的协方差值(恒为1,自己和自己肯定相关) r_1_1=C_1_1/sqrt((var(data_1)*var(data_1))) %纬度之间的相关值 r_1_2=C_1_2/sqrt((var(data_1)*var(data_2))) r_1_3=C_1_3/sqrt((var(data_1)*var(data_3))) r_3_2=C_3_2/sqrt((var(data_3)*var(data_2)))