线性规划灵敏度分析的复习要点

线性规划的灵敏度分析，其目的在于找出参数在哪一范围内发生变化时，最优基不变。

一、对参数c_s的灵敏度分析

对于单纯形表来说，最优基保持不变即意味着随着变量的波动，非基变量的检验数 r 始终保持为 >=0 的状态，否则参数波动超出了灵敏度的范围整个问题就需要重新计算；运用单纯性表的矩阵运算公式，r_i=c_i-C_B^Tyⁱ ，对该非基变量的检验数进行校核，解不等式，得到最后的结果 c 的取值范围。

若该参数对应的决策变量是基变量，那么该参数的波动会对C_B造成改变，所以此时需要对所有非基变量的检验数进行校核，求解不等式组得出参数的波动范围。

《运筹学方法与模型》 复旦大学出版社 傅家良 第二版 P₈₄ 给出了如下公式：

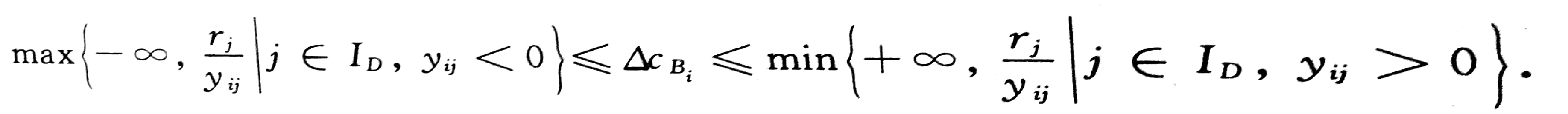
 简言之，此时的分析是用非基变量对应列的检验数除以系数，将允许的变化量放在不等号中间，（y）左负右正，（变化量）大于大的，小于小的。

 

二、对于参数b_s的灵敏度分析

基本情况类似于上述c_s，使资源变量b的变化不引起最优基的改变，而由单纯形法的矩阵运算公式，我们可以将其组成一个不等式组，由此求解出资源变量b的波动范围，同理，课本给出了与c_s 相似的公式：

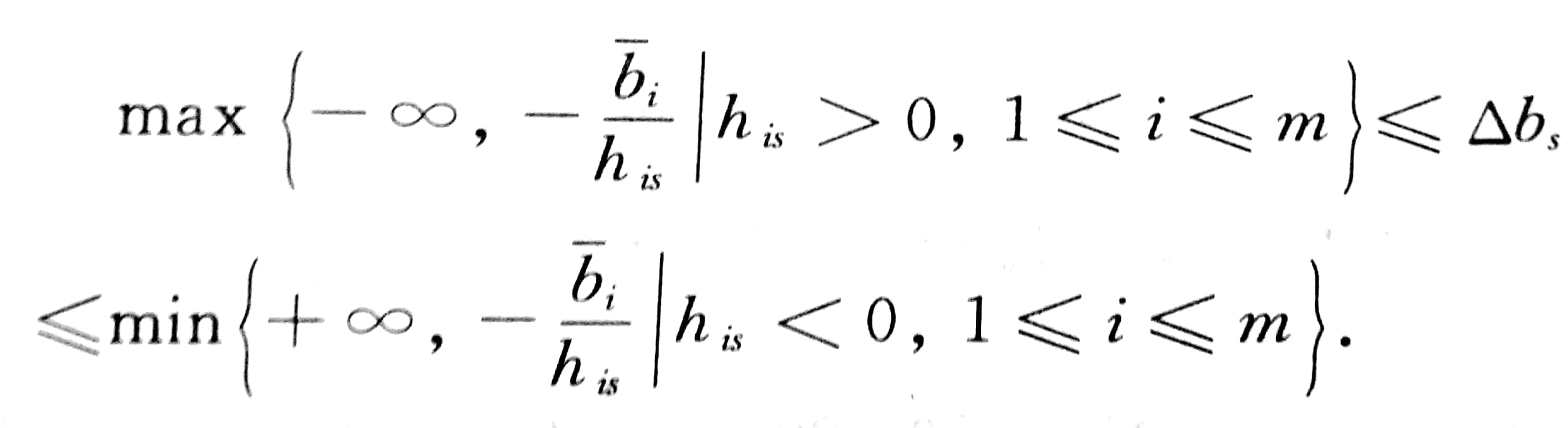
其中 B^-1 = (h_ij)_mxm = (h¹ , … , h^m) 

简言之，此时的分析使对对应的资源变量b的对应的行数 s，来寻找B^-1中的列向量h_s ，并用所有的资源变量依次与对应的h_is作比值，结果将允许的变化量放在不等号中间，（h_is）左正右负，（变化量）大于大的，小于小的。当变化量超出允许范围时，需要重新计算最优基。

 

三、影子价格

影子价格，即当资源 b_i 在波动范围内发生变化时，设 u_i* 是 i^# 资源供给量每增加一个单位，工厂最大利润 f* 所能增加的收益，于是我们称 u_i* 为关于 i^# 资源（或关于bi）的影子价格。

向量 U* = (C^TB^-1)^T 成为影子价格向量。还有一个概念叫做合理成本，与影子价格求解类似，不再赘述。