对偶问题复习要点整理
选用教材参考《运筹学方法与模型》 复旦大学出版社 傅家良 第二版
原问题模型：
一、对偶问题的转化
实例：
即为从（P）向（D）的变换
在这里我们要弄清楚怎么进行变换，显然
-
- （D）的目标函数系数是（P）的b
- （D）的系数矩阵是（P）的系数矩阵的转置
- （D）的变量的取值是与（P）的约束符号相关；（P）的 >= 对应（D）的 >= ;（P）的 = 对应（D）的 ><
- （D）的约束符号是与（P）的变量取值相关；与上一条的刚好相反
而在变换之前有一个非常关键的问题要解决，就是我们的规划问题是否满足进行变换的标准
即：最小值问题的约束必须为 >= 或 = ，决策变量的取值必须为 >= 或 ><；
最大值问题的决策变量的取值必须为 >= 或 ><，约束必须为 <= 或 = ;
二、对偶理论
这里的要点主要就是（P）和（D）的接的问题的讨论，注意各种情况下对偶问题的解的关系（定理2-3）
解主要有三种情况：
1.两个都有最优解，最优值相等
2.两者均不可行
3.一方不可行，另一方无界
这个关系大致可以用下图来表示一下
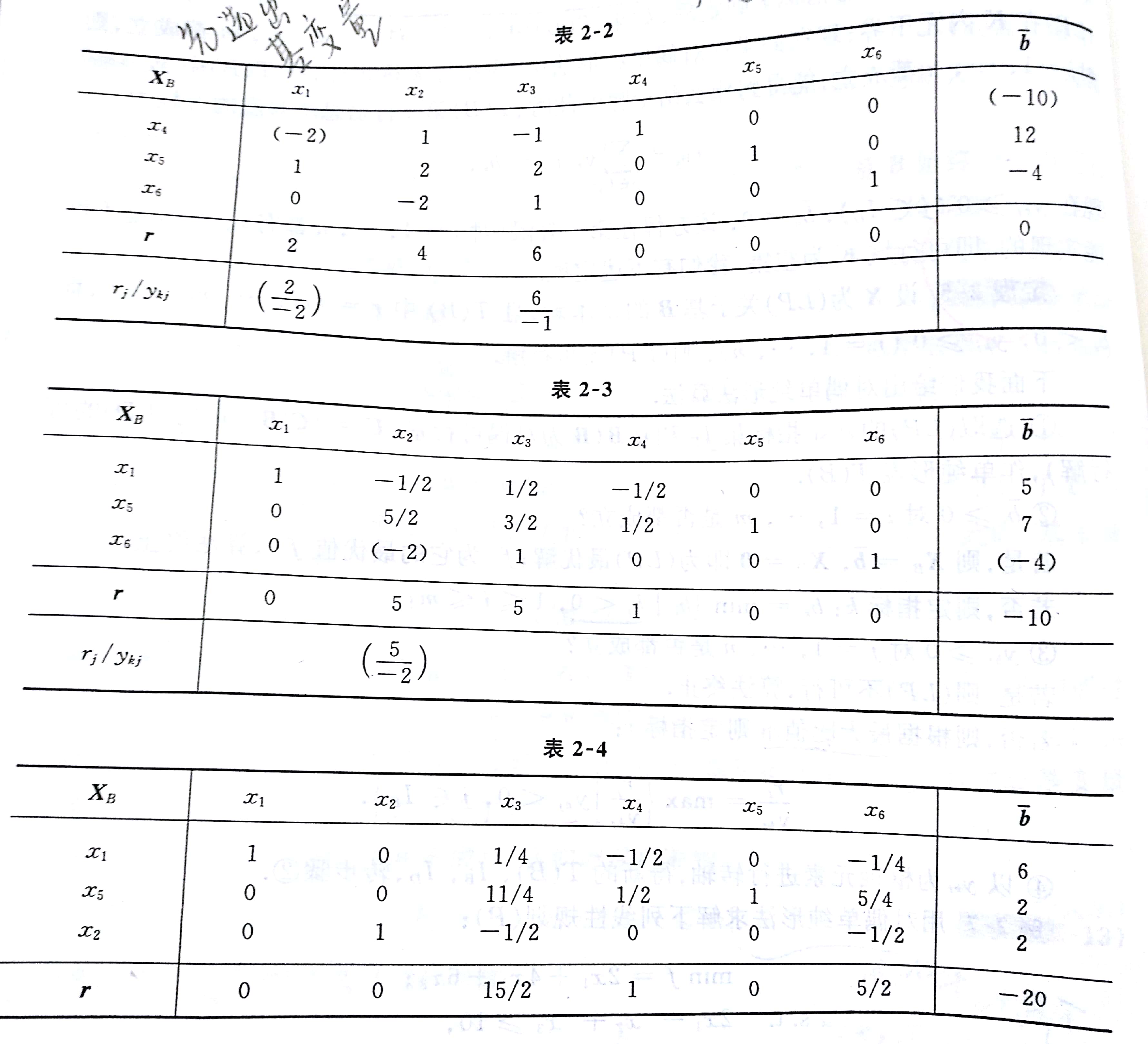
对偶问题的单纯形法：
整体而言与（LP）的单纯形法类似，但b可以为负值，从b（b<0）中选取最小值，对其所在行进行最大比值法（选取的 ykt < 0）选取转轴元素，最终使得所有得b均为正值；若在转轴过程中，b<0 但其所在行的 y 均大于零，则该对偶问题无上界，对应的（P）问题不可行
转轴过程如下图所示
对偶问题的最优解情况（即如何用（LP）求（LD）或反过来）
- （LP）问题单纯性表中的剩余变量对应检验数即为最优单纯形因子，是（LD）的最优解U*
- 我们可以用对偶单纯形法求（LP）的 B 和 B-1
- 可以在（LP）的大M法中找出（LD）的解（P79）
