朴素贝叶斯分类法 Naive Bayes ---R

朴素贝叶斯算法

 【转载时请注明来源】：http://www.cnblogs.com/runner-ljt/

   Ljt   勿忘初心  无畏未来

   作为一个初学者，水平有限，欢迎交流指正。

---

 

朴素贝叶斯分类法是一种生成学习算法。

假设：在y给定的条件下，各特征X_i 之间是相互独立的，即满足 ： P(x₁,x₂.....x_m | y)=∏ P(x_i | y)    (该算法朴素的体现之处)

原理：  贝叶斯公式        

                                

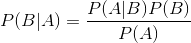
思想：对于待分类样本，求出在该样本的各特征出现的条件下，其属于每种类别的概率（P(Y_i|X)），哪种类别的概率大就将该样本判别为哪一种类别。

                               

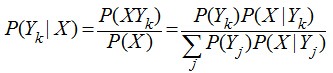
          （P(X)为x的先验概率，与Y无关，在具体计算是分母可以直接忽略，只计算分子）

---

 

P(x_i | y)的估计

（1）特征属性为离散值

       直接用每一类别中各名录出现的频率作为其概率值P(x_i|y)

（2）特征属性为连续性值

       假设特征属性服从正太分布，用各类别的样本均值及标准差作为正态分布的参数。

                                                   

                           

---

 

Laplace 平滑

     在训练样本中，某一特征的属性值可能没有出现，为了保证一个属性出现次数为0时，能够得到一个很小但是非0的概率值。

     在计算P(x_i|y)时分子加上 P_i*U ; 分母加上 U  。

     其中P_i 表示x_i 出现的先验概率，数值较大的U表示这些先验值是比较重要的，数值较小的U表示这些先验值的影响较小；

     一般情况下，P_i=1/N . (N为该特征所含有的属性类的数目)

 

---

 

R实现

包：e1071   ； 函数：naiveBayes

 

> 
> library(e1071)
> head(iris)
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa
> classifier<-naiveBayes(iris[,c(1:4)],iris[,5])
> classifier

Naive Bayes Classifier for Discrete Predictors

Call:
naiveBayes.default(x = iris[, c(1:4)], y = iris[, 5])

A-priori probabilities:
iris[, 5]
    setosa versicolor  virginica 
 0.3333333  0.3333333  0.3333333 

Conditional probabilities:
            Sepal.Length
iris[, 5]     [,1]      [,2]
  setosa     5.006 0.3524897
  versicolor 5.936 0.5161711
  virginica  6.588 0.6358796

            Sepal.Width
iris[, 5]     [,1]      [,2]
  setosa     3.428 0.3790644
  versicolor 2.770 0.3137983
  virginica  2.974 0.3224966

            Petal.Length
iris[, 5]     [,1]      [,2]
  setosa     1.462 0.1736640
  versicolor 4.260 0.4699110
  virginica  5.552 0.5518947

            Petal.Width
iris[, 5]     [,1]      [,2]
  setosa     0.246 0.1053856
  versicolor 1.326 0.1977527
  virginica  2.026 0.2746501
 
> #A-priori probabilities 为 样本中个类别出现的频率
> #Conditional probabilities （该样本的特征属于连续型值）该值表示各特征在各类别上的服从正太分布下的均值和标准差
> 
>
>
> #检验分类器效果
> table(predict(classifier,iris[,-5]),iris[,5])
            
             setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         47         3
  virginica       0          3        47
> 
> #构造新数据并进行预测
> newdata<-data.frame(Sepal.Length=5, Sepal.Width=2.3, Petal.Length=3.3, Petal.Width=1) 
> predict(classifier,newdata)
[1] versicolor
Levels: setosa versicolor virginica
> 
>