大数据之路【第十二篇】:数据挖掘--NLP文本相似度
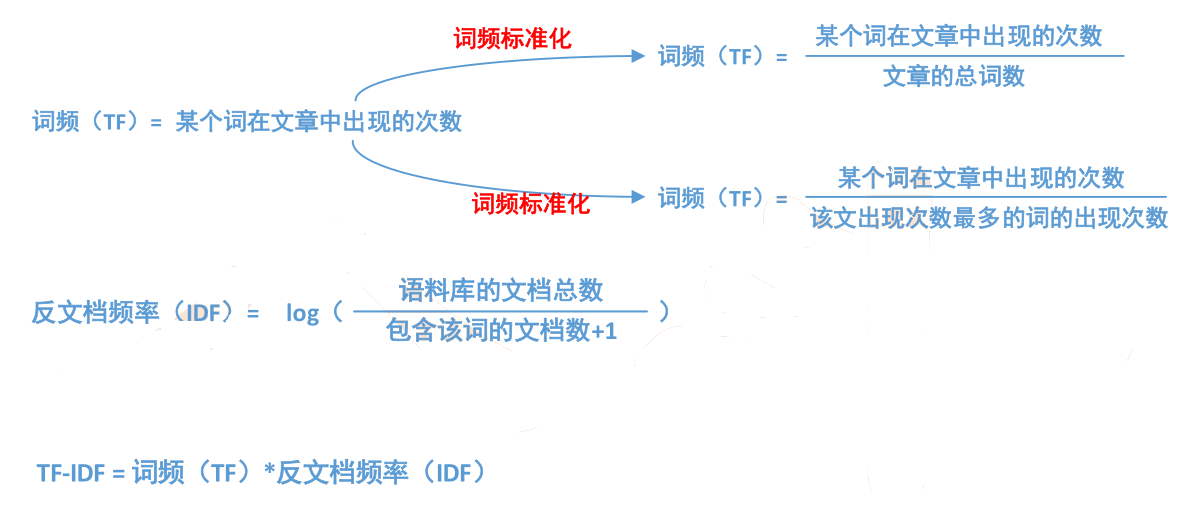
一、词频----TF
• 假设:如果一个词很重要,应该会在文章中多次出现
• 词频——TF(Term Frequency):一个词在文章中出现的次数
• 也不是绝对的!出现次数最多的是“的”“是”“在”,这类最常用的词,叫做停用词(stop words)
• 停用词对结果毫无帮助,必须过滤掉的词
• 过滤掉停用词后就一定能接近问题么?
• 进一步调整假设:如果某个词比较少见,但是它在这篇文章中多次出现,那么它很可能反映了这篇文章的特性,正是我们所需要的关键词
二、反文档频率----IDF
• 在词频的基础上,赋予每一个词的权重,进一步体现该词的重要性,
• 最常见的词(“的”、“是”、“在”)给予最小的权重
• 较常见的词(“国内”、“中国”、“报道”)给予较小的权重
• 较少见的词(“养殖”、“维基”)
• 将TF和IDF进行相乘,就得到了一个词的TF-IDF值,某个词对文章重要性越高,该值越大,于是排在前面的几个词,就是这篇文章的关键词。
计算步骤
三、LCS定义
• 最长公共子序列(Longest Common Subsequence)
• 一个序列S任意删除若干个字符得到的新序列T,则T叫做S的子序列
• 两个序列X和Y的公共子序列中,长度最长的那个,定义为X和Y的最长公共子序列
– 字符串12455与245576的最长公共子序列为2455
– 字符串acdfg与adfc的最长公共子序列为adf
• 注意区别最长公共子串(Longest Common Substring)
– 最长公共子串要求连接
四、LCS作用
• 求两个序列中最长的公共子序列算法
– 生物学家常利用该算法进行基金序列比对,以推测序列的结构、功能和演化过程。
• 描述两段文字之间的“相似度”
– 辨别抄袭,对一段文字进行修改之后,计算改动前后文字的最长公共子序列,将除此子序列
外的部分提取出来,该方法判断修改的部分
五、求解---暴力穷举法
• 假定字符串X,Y的长度分别为m,n;
• X的一个子序列即下标序列{1,2,……,m}严格递增子序列,因此,X共有2^m 个不同子序列;同理,Y有2^n 个不同子序列;
• 穷举搜索法时间复杂度O(2 ^m ∗ 2^n );
• 对X的每一个子序列,检查它是否也是Y的子序列,从而确定它是否为X和Y的公共子序列,并且在检查过程中选出最长的公共子序列;
• 复杂度高,不可用!
六、求解---动态规划法
• 字符串X,长度为m,从1开始数;
• 字符串Y,长度为n,从1开始数;
• X i =<x 1 ,……,x i >即X序列的前i个字符(1<=i<=m)(X i 计作“字符串X的i前缀”)
• Y i =<y 1 ,……,y i >即Y序列的前i个字符(1<=j<=n)(Y j 计作“字符串Y的j前缀”)
• LCS(X,Y)为字符串X和Y的最长公共子序列,即为Z=<z 1 ,……,z k >
• 如果x m = y n (最后一个字符相同),则:X ? 与Y n 的最长公共子序列Z k 的最后一个字符必定为x m (= y n )
• Zk= x m = y n
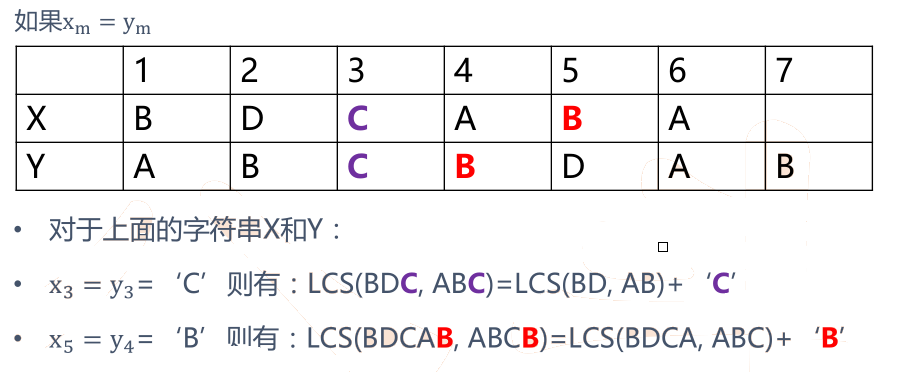
七、LCS总结分析
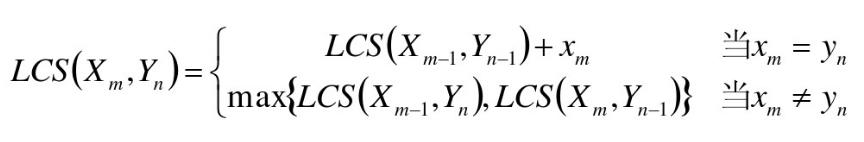
• 属于动态规划问题!
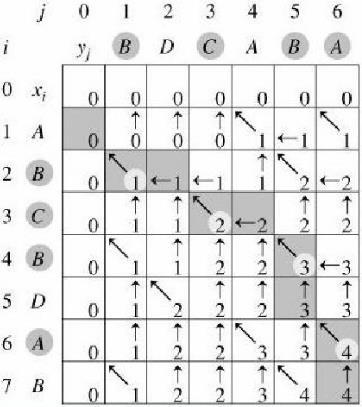
八、数据结构----二维数组
• 使用二维数组C[m,n]
• C[i,j]记录序列X i 和Y j 的最长公共子序列的长度
– 当i=0或j=0时,空虚了是X i 和Y j 的最长公共子序列,故C[i,j]=0
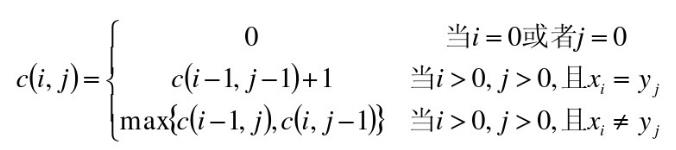
例子:
• X =<A, B, C, B, D, A, B>
• Y=<B, D, C, A, B, A>
mr_lcs mapreduce
##map.py # -*- coding: utf-8 -*- #!/usr/bin/python import sys def cal_lcs_sim(first_str, second_str): len_vv = [[0] * 50] * 50 first_str = unicode(first_str, "utf-8", errors='ignore') second_str = unicode(second_str, "utf-8", errors='ignore') len_1 = len(first_str.strip()) len_2 = len(second_str.strip()) #for a in first_str: #word = a.encode('utf-8') for i in range(1, len_1 + 1): for j in range(1, len_2 + 1): if first_str[i - 1] == second_str[j - 1]: len_vv[i][j] = 1 + len_vv[i - 1][j - 1] else: len_vv[i][j] = max(len_vv[i - 1][j], len_vv[i][j - 1]) return float(float(len_vv[len_1][len_2] * 2) / float(len_1 + len_2)) for line in sys.stdin: ss = line.strip().split('\t') if len(ss) != 2: continue first_str = ss[0].strip() second_str = ss[1].strip() sim_score = cal_lcs_sim(first_str, second_str) print '\t'.join([first_str, second_str, str(sim_score)])
#run.sh HADOOP_CMD="/usr/local/src/hadoop-1.2.1/bin/hadoop" STREAM_JAR_PATH="/usr/local/src/hadoop-1.2.1/contrib/streaming/hadoop-streaming-1.2.1.jar" INPUT_FILE_PATH_1="/lcs_input.data" OUTPUT_PATH="/lcs_output" $HADOOP_CMD fs -rmr -skipTrash $OUTPUT_PATH # Step 1. $HADOOP_CMD jar $STREAM_JAR_PATH \ -input $INPUT_FILE_PATH_1 \ -output $OUTPUT_PATH \ -mapper "python map.py" \ -jobconf "mapred.reduce.tasks=0" \ -jobconf "mapred.job.name=mr_lcs" \ -file ./map.py
mr_tfidf mapreduce
##red.py #!/usr/bin/python import sys import math current_word = None count_pool = [] sum = 0 docs_cnt = 508 for line in sys.stdin: ss = line.strip().split('\t') if len(ss) != 2: continue word, val = ss if current_word == None: current_word = word if current_word != word: for count in count_pool: sum += count idf_score = math.log(float(docs_cnt) / (float(sum) + 1)) print "%s\t%s" % (current_word, idf_score) current_word = word count_pool = [] sum = 0 count_pool.append(int(val)) for count in count_pool: sum += count idf_score = math.log(float(docs_cnt) / (float(sum) + 1)) print "%s\t%s" % (current_word, idf_score)
##run.sh HADOOP_CMD="/usr/local/src/hadoop-1.2.1/bin/hadoop" STREAM_JAR_PATH="/usr/local/src/hadoop-1.2.1/contrib/streaming/hadoop-streaming-1.2.1.jar" INPUT_FILE_PATH_1="/tfidf_input.data" OUTPUT_PATH="/tfidf_output" $HADOOP_CMD fs -rmr -skipTrash $OUTPUT_PATH # Step 1. $HADOOP_CMD jar $STREAM_JAR_PATH \ -input $INPUT_FILE_PATH_1 \ -output $OUTPUT_PATH \ -mapper "python map.py" \ -reducer "python red.py" \ -file ./map.py \ -file ./red.py


 浙公网安备 33010602011771号
浙公网安备 33010602011771号