静态点分治学习笔记

静态点分治学习笔记

点分治简介

点分治是树分治的一种。

这东西是典型的思想相对来说简单点，但是写起来巨复杂的算法，主要用于在（无根）树上解决路径相关的问题。

洛谷的模板题其实并不适合作为入门例题，我们用 P4178 Tree 做例题。

分治思想

我们不妨指令树的根为 $1$，那么树上的所有路径被分为两类：经过 $1$ 的、不经过 $1$ 的（如图）。

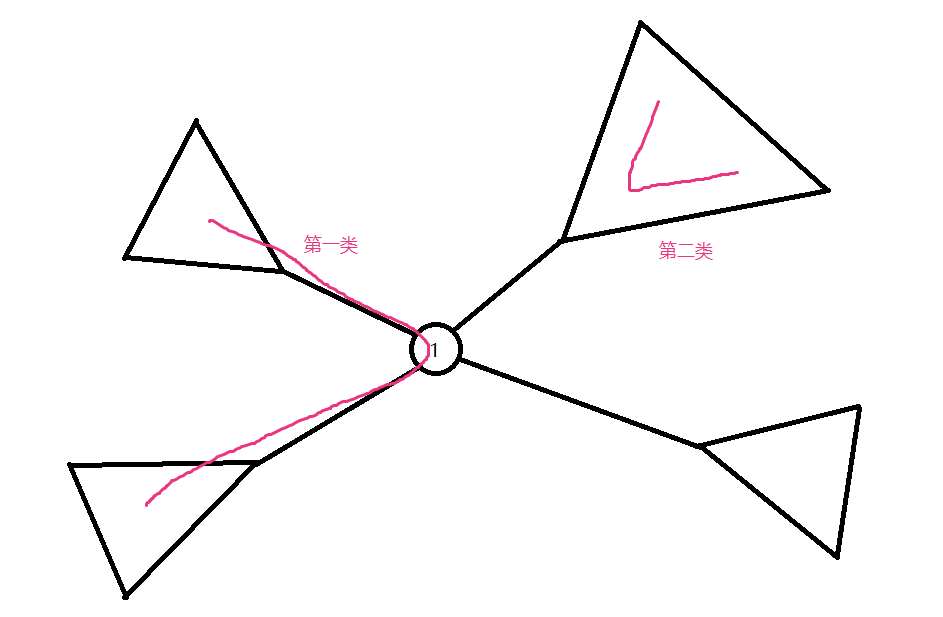
考虑对整棵树进行分治，我们先统计出所有经过 $1$ 的路径的信息，然后再对每棵子树统计它们的信息。

在例题中，我们就统计出子树内每个节点到子树根节点的距离，然后用树状数组或排序后双指针求得答案即可（详见后文），设子树大小为 $n$ 则每统计一次的时间复杂度为 $\mathcal{O}(n\log n)$。

对每一层统计的时间复杂度一般为 $\mathcal{O}(n)$ 或 $\mathcal{O}(n\log n)$，我们记为 $f(n)$（上面的例子中 $f(n)=\mathcal{O}(n\log n)$）。我们设最大的递归深度为 $g(n)$。不难得出时间复杂度为 $\mathcal{O}(f(n)g(n))$（考虑每一层每棵子树的点没有重复）。

目前来看 $g(n)=\mathcal{O}(n)$。$f(n)$ 是不好降低的，考虑降低 $g(n)$ 即递归深度。

树的重心

这其实是个前置知识，我稍微提两句。

对 $n$ 个点的无根树，设 $maxpart(u)$ 表示以节点 $u$ 为根，所有子树中点最多的数量。使 $maxpart(u)$ 取到最小值的点称为“重心”。

重心有一个性质：设 $u$ 为一个重心，则 $maxpart(u)\le\lfloor\frac{n}{2}\rfloor$。

找重心的方法就是一遍 dfs，记录子树大小和 $maxpart$。

void dfs_findroot(int u, int f, int SZ) {
    sz[u] = 1;
    int maxpart = 0;
    for(auto i : e[u]) {
        int v = get<0>(i), w = get<1>(i);
        if(v != f && !vis[v]) { // vis 的作用后面会提到
            dfs_findroot(v, u, SZ);
            sz[u] += sz[v];
            chkmax(maxpart, sz[v]);
        }
    }
    chkmax(maxpart, SZ-sz[u]);
    if(maxpart < rtsz) {
        rt = u;
        rtsz = maxpart;
    }
}

每次我们不找 $1$、$1$ 的儿子、$1$ 的儿子的儿子……当根节点，而是找当前分治到的这棵树的重心当根节点。

$f(n)$ 依然是 $\mathcal{O}(n)$ 或 $\mathcal{O}(n\log n)$ 不会变，$g(n)$ 的话根据 $maxpart(u)\le\lfloor\frac{n}{2}\rfloor$ 的性质，每一层点数会除以二，易知 $g(n)=\mathcal{O}(\log n)$。

于是 $T(n)=f(n)g(n)$，就变成了 $\mathcal{O}(n\log n)$ 或 $\mathcal{O}(n\log^2n)$ 了！例题中就是 $\mathcal{O}(n\log^2n)$。

统计答案

统计答案

讲了这么多，还没说怎么统计答案。

例题中有两种统计答案的方法。

第一种解法

我们设当前的根为 $rt$，处理 $d_u$ 为 $u$ 到 $rt$ 的距离。

从 $rt$ 的第一棵子树开始依次统计，对第 $i$ 棵子树的每个点 $u$，在第 $1\sim i-1$ 棵子树中找到所有满足 $d_u+d_v\le k$ 的点 $v$ 的个数累加。

具体地就是用一棵树状数组维护，下标是到根距离，值是到根距离是这么多的点的数量。

注意路径的一端可以是 $rt$。另外注意在回溯的时候清空树状数组。

$f(n)=\mathcal{O}(n\log k)$。

这种写法我（好像）没写过。

第二种解法

对当前分治到的树的所有节点按 $d_u$ 排序，此时 $d_u$ 单调递增，那么 $d_v\le k-d_u$ 这个上限单调递减，用双指针统计 $d_u+d_v\le k$ 的点数即可。

发现多统计了一些，就是可能 $u,v$ 在同一个子树内，它们之间路径不经过 $rt$ 但也被统计了，考虑进行容斥，我们在递归点分治每棵子树前把答案减掉子树内部 $d_u+d_v\le k$ 的点数即可。

$f(n)=\mathcal{O}(n\log n)$。

void dfs_dis(int u, int f) {
    d.push_back(dis[u]);
    for(auto i : e[u]) {
        int v = get<0>(i), w = get<1>(i);
        if(v != f && !vis[v]) {
            dis[v] = dis[u] + w;
            dfs_dis(v, u);
        }
    }
}
int calc(int u) {
    d.clear();
    dfs_dis(u, 0);
    sort(d.begin(), d.end());
    int sz = d.size();
    int L = 0, R = sz - 1, ans = 0;
    while(L < R) {
        while(L < R && d[L] + d[R] > k) --R;
        ans += R - L;
        ++L;
    }
    return ans;
}
int divid(int u, int SZ) {
    rtsz = SZ;
    dfs_findroot(u, 0, SZ);
    u = rt;
    dis[u] = 0;
    vis[u] = 1; // 标记这个点被分治过，相当于把整棵树从这个点断开得到若干棵子树，在 dfs_findroot 和 dfs_dis 时不能经过这个点
    int ans = calc(u); // 统计整棵树的答案
    for(auto i : e[u]) {
        int v = get<0>(i), w = get<1>(i);
        if(!vis[v]) {
            ans -= calc(v); // 容斥，减掉算多了的答案
            ans += divid(v, d.size());
        }
    }
    return ans;
}

完整代码

//By: Luogu@rui_er(122461)
#include <bits/stdc++.h>
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
#define debug printf("Running %s on line %d...\n",__FUNCTION__,__LINE__)
#define fileIO(s) do{freopen(s".in","r",stdin);freopen(s".out","w",stdout);}while(false)
using namespace std;
typedef long long ll;
const int N = 4e4+5;

int n, k, dis[N], sz[N], vis[N], rt, rtsz;
vector<int> d;
vector<tuple<int, int> > e[N]; 
template<typename T> void chkmin(T& x, T y) {if(x > y) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}
void dfs_findroot(int u, int f, int SZ) {
    sz[u] = 1;
    int maxpart = 0;
    for(auto i : e[u]) {
        int v = get<0>(i), w = get<1>(i);
        if(v != f && !vis[v]) {
            dfs_findroot(v, u, SZ);
            sz[u] += sz[v];
            chkmax(maxpart, sz[v]);
        }
    }
    chkmax(maxpart, SZ-sz[u]);
    if(maxpart < rtsz) {
        rt = u;
        rtsz = maxpart;
    }
}
void dfs_dis(int u, int f) {
    d.push_back(dis[u]);
    for(auto i : e[u]) {
        int v = get<0>(i), w = get<1>(i);
        if(v != f && !vis[v]) {
            dis[v] = dis[u] + w;
            dfs_dis(v, u);
        }
    }
}
int calc(int u) {
    d.clear();
    dfs_dis(u, 0);
    sort(d.begin(), d.end());
    int sz = d.size();
    int L = 0, R = sz - 1, ans = 0;
    while(L < R) {
        while(L < R && d[L] + d[R] > k) --R;
        ans += R - L;
        ++L;
    }
    return ans;
}
int divid(int u, int SZ) {
    rtsz = SZ;
    dfs_findroot(u, 0, SZ);
    u = rt;
    dis[u] = 0;
    vis[u] = 1;
    int ans = calc(u);
    for(auto i : e[u]) {
        int v = get<0>(i), w = get<1>(i);
        if(!vis[v]) {
            ans -= calc(v);
            ans += divid(v, d.size());
        }
    }
    return ans;
}

int main() {
    scanf("%d", &n);
    rep(i, 1, n-1) {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        e[u].push_back(make_tuple(v, w));
        e[v].push_back(make_tuple(u, w));
    }
    scanf("%d", &k);
    printf("%d\n", divid(1, n));
    return 0;
}