网络流(最大流、最小费用流、上下界网络流)学习笔记(费用流、上下界以及它们的建模还没写)
网络流(最大流、最小费用流、上下界网络流)学习笔记
基本概念
网络
网络是一个有向图 \(G=(V,E)\),其中每条边 \((u,v)\in E\) 都有一个容量 \(c(u,v)\),若 \((u,v)\notin E\) 则 \(c(u,v)=0\)。
网络图中有两个特殊的点:源点 \(s\in V\) 和汇点 \(t\in V\)(\(s\ne t\))。
流
设 \(f(u,v)\) 是 \(V\times V\to\R\) 的函数,且满足如下性质:
- 容量限制:\(f(u,v)\le c(u,v)\)。
- 斜对称性:\(f(u,v)=-f(v,u)\)。
- 流量守恒:\(\forall u\in V\setminus\{s,t\},f^{in}(u)=\sum\limits_{(v,u)\in E}f(v,u)=\sum\limits_{(u,w)\in E}f(u,w)=f^{out}(u)\)。
则称 \(f\) 是网络 \(G\) 的流函数。\(f(u,v)\) 称为边 \((u,v)\) 的流量,\(c(u,v)-f(u,v)\) 称为边 \((u,v)\) 的剩余容量。网络的流量记作 \(V(f)=\sum\limits_{(s,u)\in E}f(s,u)=\sum\limits_{(v,t)\in E}f(v,t)\)。
最大流
简介
最大流问题是求源点到汇点最大流量的问题。
Ford-Fulkerson 方法
FF 方法思路
FF 方法的核心思路是构建一个初始的流,不断进行改进,直到得到最大流。
定义 \(\operatorname{bottleneck}(p,f)\) 为流 \(f\) 状态下,路径 \(p\) 经过的所有边中的最小剩余容量。
那么我们不断增广流 \(f\) 中的源点到汇点的路径 \(p\),使得流量增加 \(\operatorname{bottleneck}(p,f)\)。
但是这样是有问题的,例如对于这张网络:(边上标注:流量/容量)
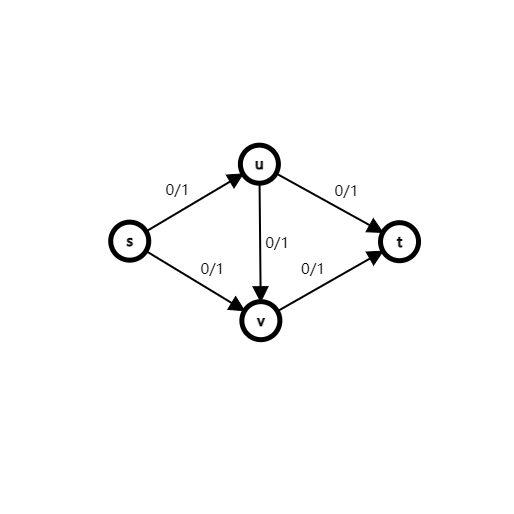
显然,它的最大流如下图所示:
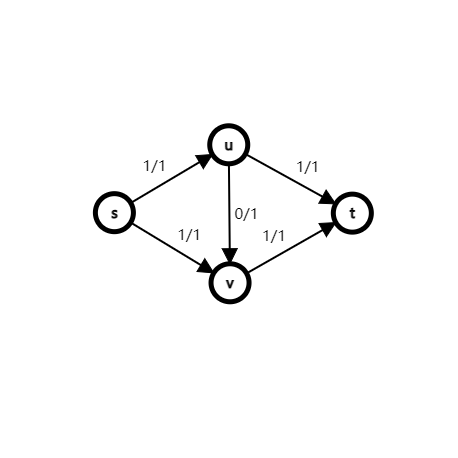
但是,如果第一次找到的增广路是这样的,则源点和汇点被阻塞,无法继续增广,所得流量错误:
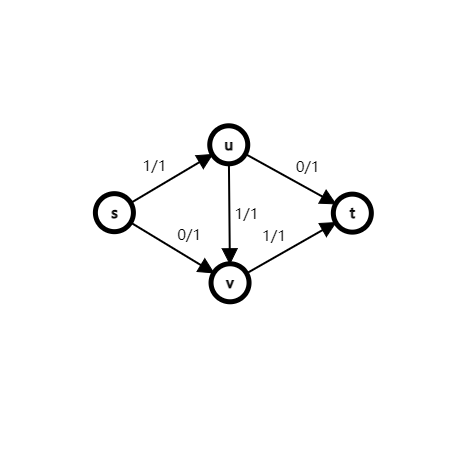
我们发现,现在的方法会错走不该走的路径,因此我们引入反向边和剩余图用于退流。
对于有向图 \(G=(V,E)\) 和流 \(f\),我们定义它的剩余图 \(G_f=(V,E')\)。对于原图中每条边 \((u,v)\in E\),在剩余图中按如下规则添加至多两条边:
- 正向边:如果 \(f(u,v) < c(u,v)\),则添加一条边 \((u,v)\),容量 \(c'(u,v)=c(u,v)-f(u,v)\)。
- 反向边:如果 \(f(u,v) > 0\),则添加一条边 \((v,u)\),容量 \(c'(v,u)=f(u,v)\)。
例如,对于上面这个走了不该走的路径的流:

它的剩余图如下:
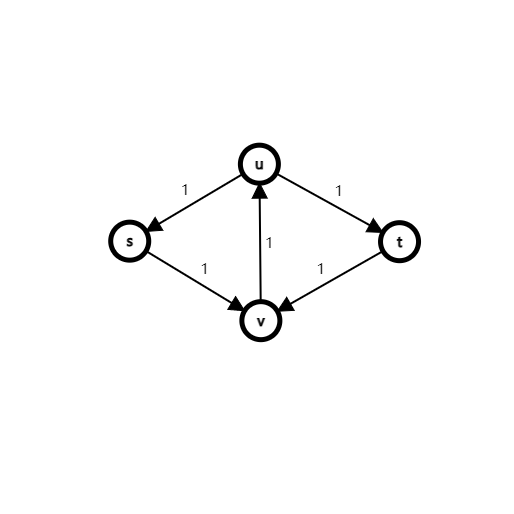
就可以继续增广了。
总结 FF 方法流程
- 初始时所有 \(f(u,v)=0\)。
- 若 \(G_f\) 中存在源点到汇点的路径,任选一条路径进行增广。
- 若 \(G_f\) 中不存在源点到汇点的路径,此时的 \(f\) 即为最大流,方法结束。
复杂度和缺陷说明
(一)当容量 \(c(u,v)\in\N^+\) 时
我们很容易构造一张网络把 FF 方法卡掉:
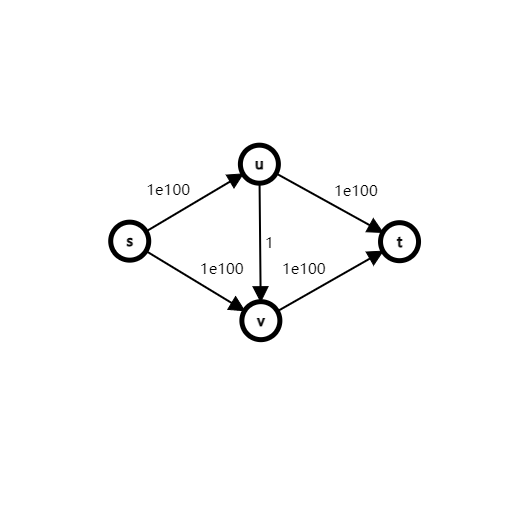
如果依次增广 \(s\to u\to v\to t,s\to v\to u\to t,s\to u\to v\to t,\cdots\),显然需要增广 \(2\times {10}^{100}\) 次。
具体地,假设 \(n,m,f\) 为点数、边数、最大流流量,则 FF 方法在容量为整数时的复杂度为 \(\mathcal O(mf)\)。
(二)当容量 \(c(u,v)\in\R^+\) 时
构造下面这张网络:
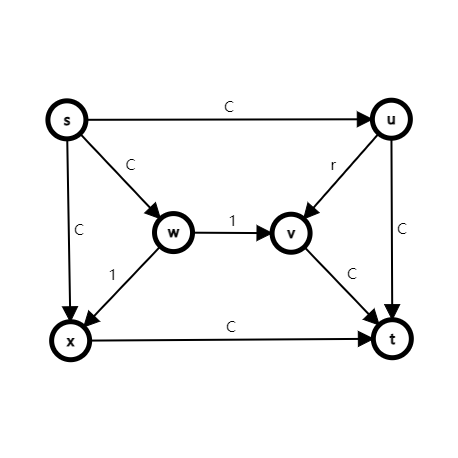
其中 \(C\) 是足够大的整数(例如 \({10}^{100}\)),\(r=\dfrac{\sqrt{5}-1}{2}\approx 0.618\),显然有 \(r^2=1-r\) 且 \(\cdots < r^4 < r^3 < r^2 < r < 1\)。
如果依次增广 \(s\to u\to v\to w\to x\to t,s\to w\to v\to u\to t,s\to u\to v\to w\to x\to t,s\to x\to w\to v\to t,s\to u\to v\to w\to x\to t,\cdots\),则方法最终会收敛到一个小于最大流的流,方法错误。
具体地,假设增广了 \(1+4k\) 次,则收敛到的流:
而最大流显然为 \(2C+1\)。
闲话
虽然 FF 方法有种种缺陷,但是 CF 上还真有一道卡掉了后面要讲的 EK、Dinic 而正解 FF 的题(其实是先 Dinic 然后再 FF):CF1383F Special Edges。
Edmonds-Karp 算法
EK 算法
相比于 FF 方法,EK 算法在寻找增广路时并不是随便找一条,而是通过 BFS 的方式找最短的一条。
复杂度
EK 算法的时间复杂度为 \(\mathcal O(nm^2)\)。
这里简单说一下证明方法:
发现 EK 算法执行过程中,任何点在剩余图中的层数单调不降。
对于每条边 \((u,v)\),其连续作为 \(\operatorname{bottleneck}\) 时,\(u\) 所在层数至少增加 \(2\)。又显然层数最多为 \(n\)。
因此,对于每条边 \((u,v)\),它作为 \(\operatorname{bottleneck}\) 的次数不超过 \(\dfrac{n}{2}\) 次。
共 \(m\) 条边,最多增广 \(\mathcal O(nm)\) 次,每次 BFS 找增广路复杂度为 \(\mathcal O(m)\),故总复杂度为 \(\mathcal O(nm^2)\)。
代码
好久没写过最大流的 EK 了,放个几年前的代码凑合看吧:
#include <bits/stdc++.h>
using namespace std;
#define inf 1073741823
int n, m, s, t;
struct Node
{
int v;
int val;
int next;
}node[201010];
int top = 1, head[101010];
inline void addedge(int u, int v, int val)
{
node[++top].v = v;
node[top].val = val;
node[top].next = head[u];
head[u] = top;
}
inline int Qread(void)
{
int x = 0;
char c = getchar();
while(c > '9' || c < '0') c = getchar();
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
return x;
}
int inque[101010];
struct Pre
{
int v;
int edge;
}pre[101010];
inline bool BFS(void)
{
queue<int> q;
memset(inque, 0, sizeof inque);
memset(pre, -1, sizeof pre);
inque[s] = 1;
q.push(s);
while(!q.empty())
{
int u = q.front();
q.pop();
for(int i=head[u];i;i=node[i].next)
{
int d = node[i].v;
if(!inque[d] && node[i].val)
{
pre[d].v = u;
pre[d].edge = i;
if(d == t) return true;
inque[d] = 1;
q.push(d);
}
}
}
return false;
}
int EK(void)
{
int ans = 0;
while(BFS())
{
int minx = inf;
for(int i=t;i!=s;i=pre[i].v)
minx = min(minx, node[pre[i].edge].val);
for(int i=t;i!=s;i=pre[i].v)
{
node[pre[i].edge].val -= minx;
node[pre[i].edge^1].val += minx;
}
ans += minx;
}
return ans;
}
int main(void)
{
register int i;
n = Qread();
m = Qread();
s = Qread();
t = Qread();
int u, v, w;
for(i=1;i<=m;i++)
{
u = Qread();
v = Qread();
w = Qread();
addedge(u, v, w);
addedge(v, u, 0);
}
cout<<EK()<<endl;
return 0;
}
Dinic 算法
Dinic 算法
Dinic 算法通过在剩余图 \(G_f\) 上建立分层网络 \(G_L\),充分利用了 BFS 的信息。
首先定义剩余图 \(G_f\) 上的分层网络 \(G_L\):在 \(G_f\) 上进行 BFS 分层,从层 \(d\) 节点连向层 \(d+1\) 节点的边被保留在 \(G_L\) 中。容易发现 \(G_L\) 中包含了所有 \(s\to u\) 的最短路。
Dinic 算法的一个阶段执行如下操作:
- 在 \(G_f\) 上做 BFS 建立 \(G_L\)。
- 在 \(G_L\) 上做 DFS 寻找阻塞流 \(f'\),使用 \(f'\) 增广 \(f\)。
其中阻塞流 \(f'\) 满足它的剩余图中源点和汇点被阻塞,也就是不存在其他增广路。
复杂度
Dinic 算法的时间复杂度为 \(\mathcal O(n^2m)\)。
这里简单说一下证明方法:
每个算法阶段至少使得汇点 \(t\) 的层次增加 \(1\),因此最多有 \(\mathcal O(n)\) 个算法阶段。
每个算法阶段中:
- BFS 构建分层网络 \(G_L\) 复杂度为 \(\mathcal O(m)\)。
- 寻找阻塞流复杂度为 \(\mathcal O(nm)\)。
- 其中,DFS 寻找一条路径复杂度为 \(\mathcal O(n)\)。
- 每条路径中,至少一条边作为 \(\operatorname{bottleneck}\) 会满流,因此最多 \(\mathcal O(m)\) 条路径。
特别地,Dinic 算法解决二分图最大匹配问题的时间复杂度为 \(\mathcal O(m\sqrt{n})\),优于匈牙利算法的 \(\mathcal O(nm)\)。
算法优化
Dinic 算法有两个常见的优化:
- 多路增广:每找到一条增广路,如果剩余容量没有用完,可以继续找增广路。
- 当前弧优化:在一张 \(G_L\) 中,如果一条边被增广过,它就没有可能被增广第二次,下次增广时可以不必考虑这些边。
代码
//By: Luogu@rui_er(122461)
#include <bits/stdc++.h>
#define rep(x,y,z) for(ll x=y;x<=z;x++)
#define per(x,y,z) for(ll x=y;x>=z;x--)
#define debug printf("Running %s on line %d...\n",__FUNCTION__,__LINE__)
#define fileIO(s) do{freopen(s".in","r",stdin);freopen(s".out","w",stdout);}while(false)
using namespace std;
typedef long long ll;
const ll N = 205, M = 1e4+5, inf = 0x3f3f3f3f3f3f3f3fll;
ll n, m, s, t, dis[N], now[N];
queue<ll> q;
template<typename T> void chkmin(T& x, T y) {if(x > y) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}
struct Edge {
ll v, w, nxt;
Edge(ll a=0, ll b=0, ll c=0) : v(a), w(b), nxt(c) {}
~Edge() {}
}e[M];
ll h[N], ne = 1;
void add(ll u, ll v, ll w) {
e[++ne] = Edge(v, w, h[u]); h[u] = ne;
e[++ne] = Edge(u, 0, h[v]); h[v] = ne;
}
ll dfs(ll u, ll lim) {
if(!lim || u == t) return lim;
ll res = 0;
for(ll i=now[u];i;now[u]=i=e[i].nxt) {
ll v = e[i].v, w = e[i].w;
if(dis[v] == dis[u] + 1) {
ll qwq = dfs(v, min(lim, w));
res += qwq; lim -= qwq;
e[i].w -= qwq; e[i^1].w += qwq;
if(!lim) break;
}
}
return res;
}
bool bfs() {
memset(dis, 0x3f, sizeof(dis));
memcpy(now, h, sizeof(h));
while(!q.empty()) q.pop();
dis[s] = 0;
q.push(s);
while(!q.empty()) {
ll u = q.front(); q.pop();
for(ll i=h[u];i;i=e[i].nxt) {
ll v = e[i].v, w = e[i].w;
if(w && dis[v] == inf) {
dis[v] = dis[u] + 1;
q.push(v);
}
}
}
return dis[t] < inf;
}
ll dinic() {
ll flow = 0;
while(bfs()) flow += dfs(s, inf);
return flow;
}
int main() {
scanf("%lld%lld%lld%lld", &n, &m, &s, &t);
rep(i, 1, m) {
ll u, v, w;
scanf("%lld%lld%lld", &u, &v, &w);
add(u, v, w);
}
printf("%lld\n", dinic());
return 0;
}
其他最大流算法
其他最大流算法还有 MPM(\(\mathcal O(n^3)\))、ISAP(\(\mathcal O(n^2m)\))、Push-Relabel 预流推进(\(\mathcal O(n^3)\))、HLPP 最高标号预流推进(\(\mathcal O(n^2\sqrt{m})\))、近期发明的近线性网络流算法(\(\mathcal O(m^{1+o(1)})\)) 等,但是 Dinic 一般跑不满,实现相对容易且效率较高,在一般的算法竞赛题里完全够用了,因此本博客不会介绍。好吧其实是我不会。
最小割
定义
一个 \(s-t\) 的切割是点集 \(V\) 的一个划分 \((A,B)\),其中 \(s\in A,t\in B\)。定义切割 \((A,B)\) 的容量为 \(c(A,B)=\sum\limits_{u\in A,v\in B,(u,v)\in E}c(u,v)\),也就是所有从 \(A\) 指向 \(B\) 的边的容量之和(注意从 \(B\) 指向 \(A\) 的不算)。
例如对于下图:
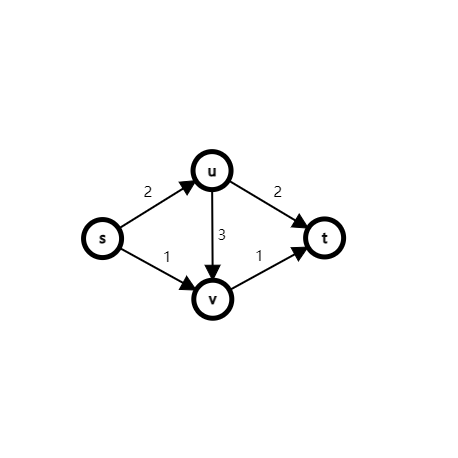
如果令 \(A=\{s,v\},B=\{u,t\}\),则 \(c(A,B)=c(s,u)+c(v,t)=2+1=3\)。
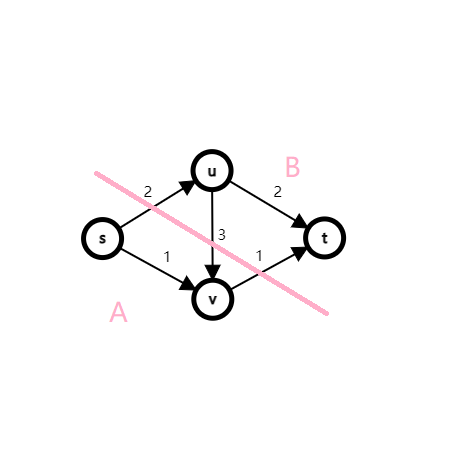
顾名思义,最小割就是要求解割的最小容量。
引理一
令 \(f\) 为一个流,\((A,B)\) 为任意一个 \(s-t\) 切割,则横跨切割的流量与网络的流量相等,即 \(V(f)=f^{out}(A)-f^{in}(A)\)。
例如下面这张图中,\(V(f)=2+1-1=2\):
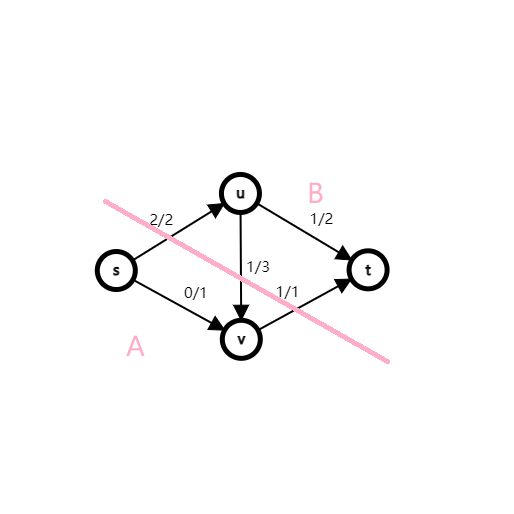
证明:
引理二
令 \(f\) 为一个流,\((A,B)\) 为任意一个 \(s-t\) 切割,则 \(V(f)\le c(A,B)\)。
证明:
最大流最小割定理
\(f\) 为 \(G\) 的最大流 \(\iff\) 存在切割 \((A,B)\) 使得 \(V(f)=c(A,B)\)。
证明:
FF 方法结束后,\(G_f\) 中没有 \(s\) 到 \(t\) 路径。
令 \(A\) 为 \(G_f\) 上从 \(s\) 可达的点,\(B=V\setminus A\),则 \((A,B)\) 为一个切割。
考虑横跨切割的边 \((u,v)\in E\):
- 若 \(u\in A,v\in B\),则 \(f(u,v)=c(u,v)\)。
- 若 \(v\in A,u\in B\),则 \(f(u,v)=0\)。
因此:
最小割问题
因此最小割问题可以转化为最大流问题进行求解,我们也可以根据上面给出一种构造。
最大流与最小割建模
二分图最大匹配 | P2756 飞行员配对方案问题
匈牙利算法的时间复杂度为 \(\mathcal O(n^3)\) 或 \(\mathcal O(nm)\)。
考虑这样一种建模:
- 源点向二分图左部点连容量为 \(1\) 的边。
- 二分图右部点向汇点连容量为 \(1\) 的边。
- 二分图左部点向与之相连的二分图右部点连容量为 \(1\) 的边。
时间复杂度为 \(\mathcal O(m\sqrt{n})\)。
这个是最简单的最大流建模之一。
二者选其一问题 | P2057 [SHOI2007] 善意的投票 / [JLOI2010] 冠军调查
将若干个物品分为 \(A,B\) 两类,其中有三种代价:
- 第 \(i\) 个物品分到 \(A\) 类,产生 \(a_i\) 的代价。
- 第 \(i\) 个物品分到 \(B\) 类,产生 \(b_i\) 的代价。
- 第 \(u_i\) 个物品和第 \(v_i\) 个物品分到不同类,产生 \(c_i\) 的代价。
要使得总代价最小。
考虑这样一种建模:
- 源点向每个物品连容量为 \(b_i\) 的边。
- 每个物品向汇点连容量为 \(a_i\) 的边。
- \(u_i\) 和 \(v_i\) 互相连容量为 \(c_i\) 的边。
在 Dinic 算法结束后,点被分为两类:从源点可达的、从源点不可达的。它们对应了 \(A,B\) 两类。容易发现,一个划分的割就是这种分类方案的代价,我们求最小割即可。
P1402 酒店之王
有 \(n\) 个人,每个人有若干个想住的房间、若干道想吃的菜。每个人住一个房间,吃一道菜。一个房间只能住一个人,一道菜也只能一个人吃,求最多满足多少人要求。
考虑这样一种建模:
- 源点向每个房间连容量为 \(1\) 的边。
- 每道菜向汇点连容量为 \(1\) 的边。
- 每个房间向每个想住这个房间的人连容量为 \(1\) 的边。
- 每个人想这个人想吃的菜连容量为 \(1\) 的边。
但是这个建模是错误的,原因是没有限制一个人只能住一个房间,吃一道菜。我们考虑拆点(这是非常重要的建模思想),将每个人拆成两个点,两点之间连容量为 \(1\) 的边,这样就限制了每个人只能住一个房间,吃一道菜。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号